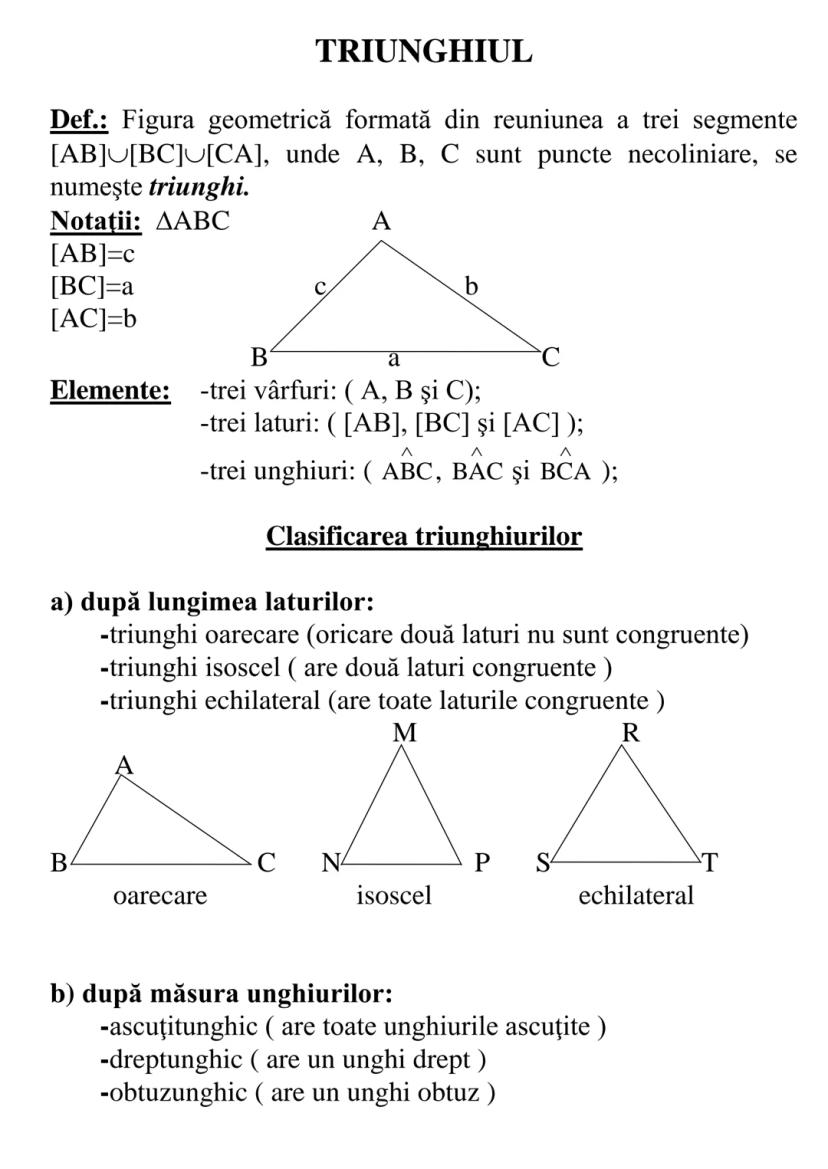
Ce este un triunghi
Un triunghi este o figură geometrică formată din trei segmente [AB], [BC] și [CA], unde punctele A, B și C nu sunt coliniare. Notăm triunghiul cu simbolul ΔΑВС.
Fiecare triunghi are trei vârfuri (A, B și C), trei laturi ([AB], [BC] și [AC]) și trei unghiuri (∠ABC, ∠BAC și ∠BCA). Laturile se notează de obicei cu litere mici: [AB]=c, [BC]=a și [AC]=b.
Triunghiurile pot fi clasificate după lungimea laturilor în:
- Triunghi oarecare - toate laturile au lungimi diferite
- Triunghi isoscel - are două laturi egale
- Triunghi echilateral - are toate cele trei laturi egale
De asemenea, după măsura unghiurilor, triunghiurile pot fi:
- Ascuțitunghice - toate unghiurile sunt ascuțite (sub 90°)
- Dreptunghice - au un unghi drept (de 90°)
- Obtuzunghice - au un unghi obtuz (peste 90°)
Știai că? Suma măsurilor unghiurilor în orice triunghi este întotdeauna 180°!









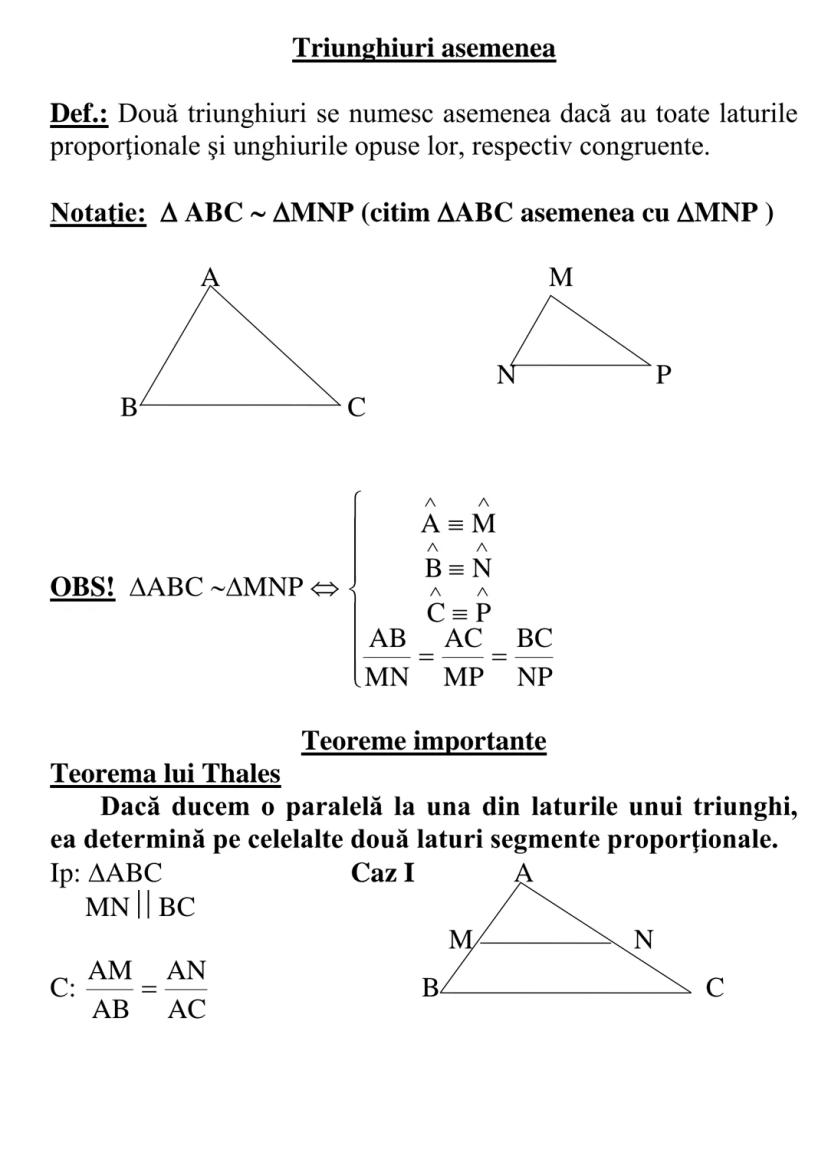


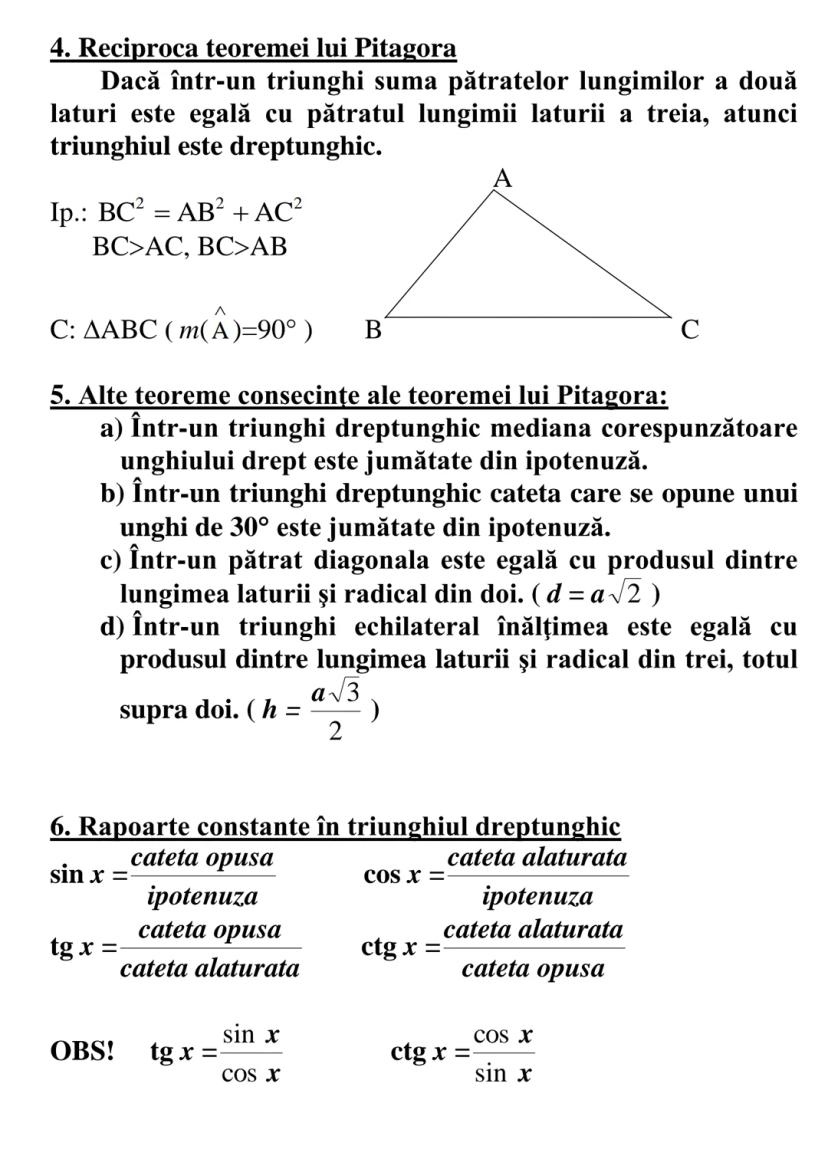
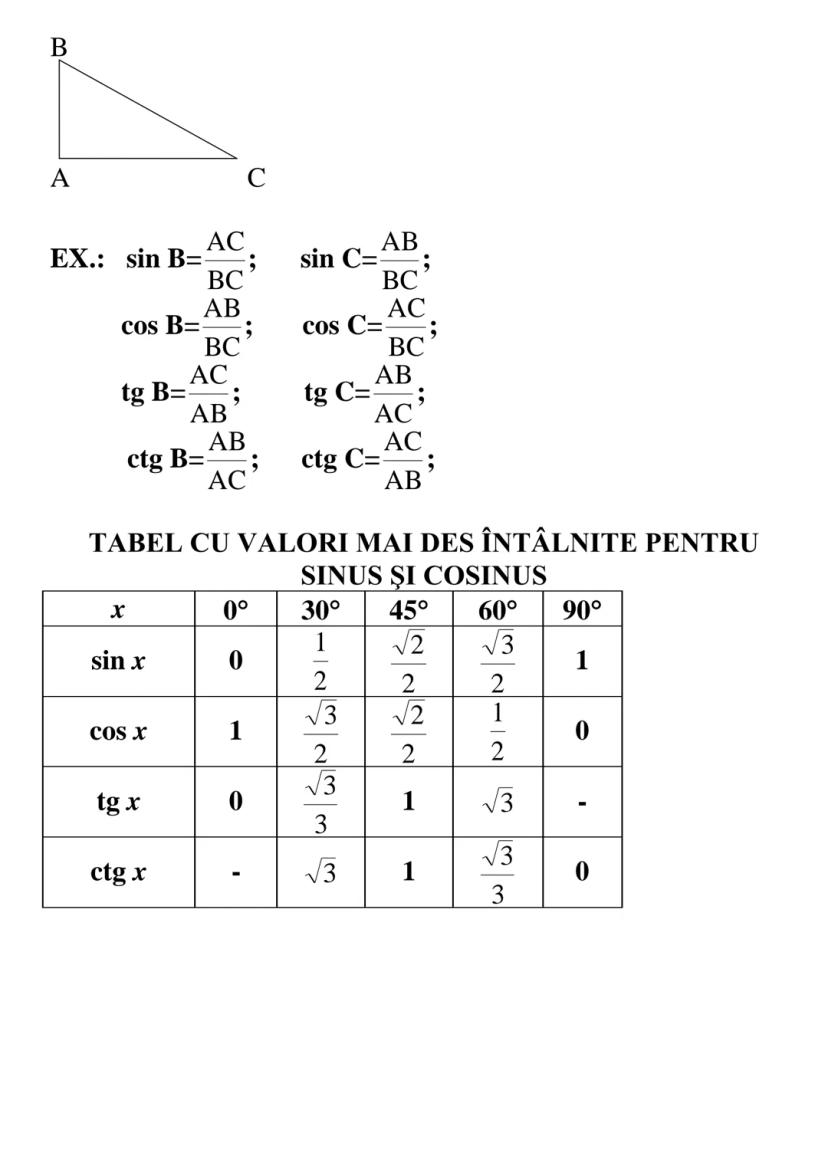



![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_1.webp&w=2048&q=75)
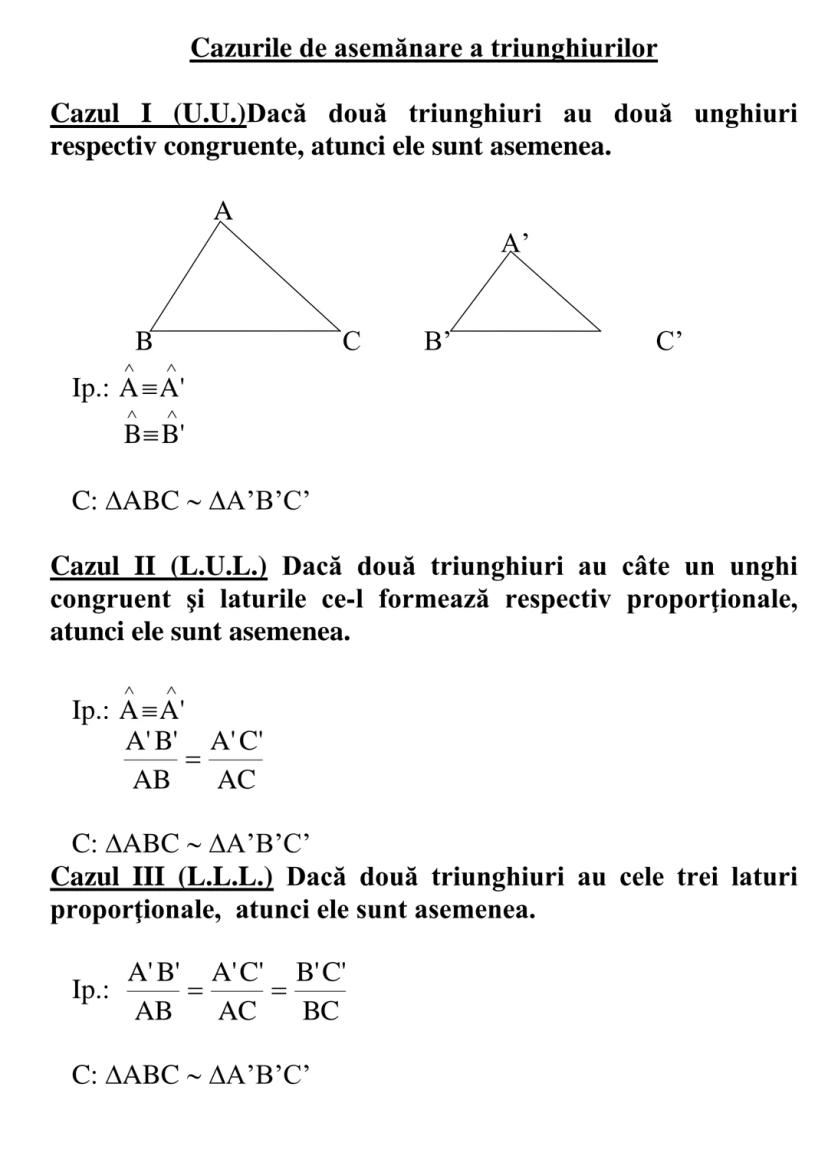
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_2.webp&w=2048&q=75)
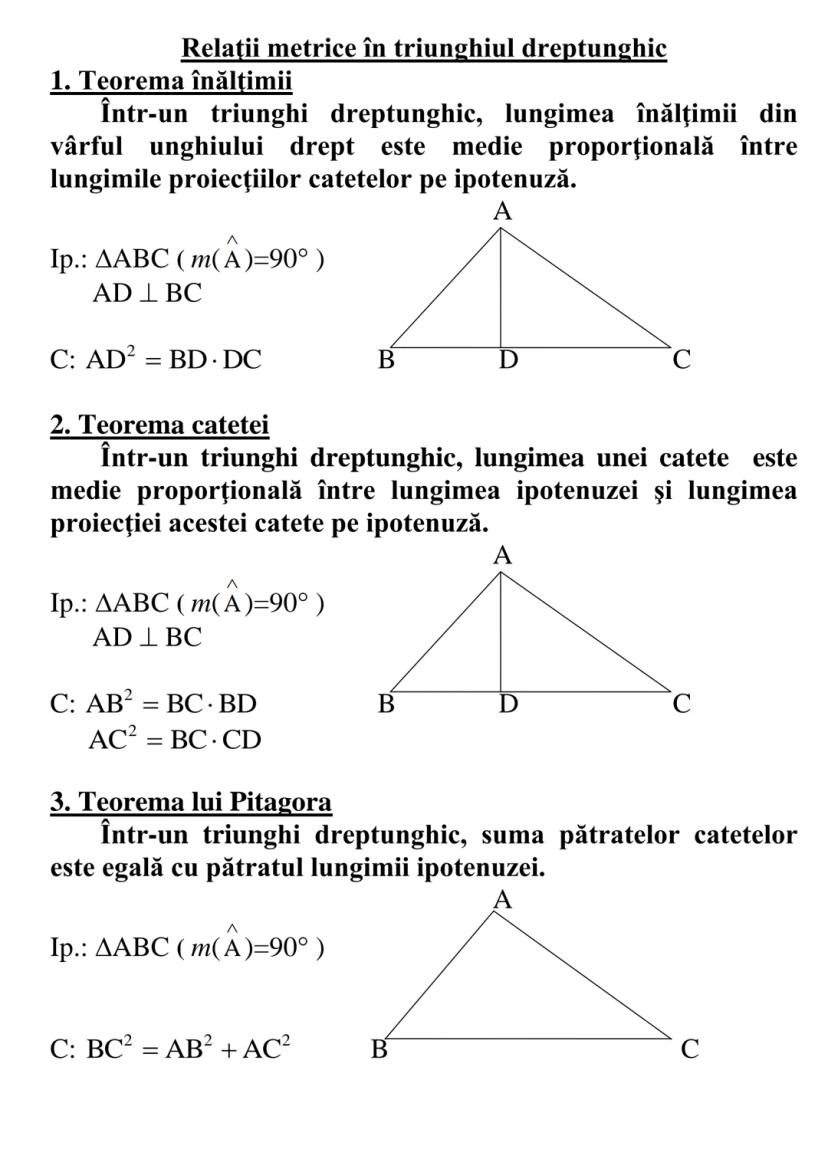
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_3.webp&w=2048&q=75)
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_4.webp&w=2048&q=75)
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_5.webp&w=2048&q=75)
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_6.webp&w=2048&q=75)
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_7.webp&w=2048&q=75)
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_8.webp&w=2048&q=75)
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_9.webp&w=2048&q=75)
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_10.webp&w=2048&q=75)
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_11.webp&w=2048&q=75)
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_12.webp&w=2048&q=75)
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_13.webp&w=2048&q=75)
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_14.webp&w=2048&q=75)
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_15.webp&w=2048&q=75)
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_16.webp&w=2048&q=75)
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_17.webp&w=2048&q=75)
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_18.webp&w=2048&q=75)
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_19.webp&w=2048&q=75)
![TRIUNGHIUL
Def.: Figura geometrică formată din reuniunea a trei segmente
[AB][BC][CA], unde A, B, C sunt puncte necoliniare, se
numeşte triu](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F0195e876-45b3-7e0c-8269-ef14fd008bc2_image_page_20.webp&w=2048&q=75)