Mulțimea numerelor naturale și puteri

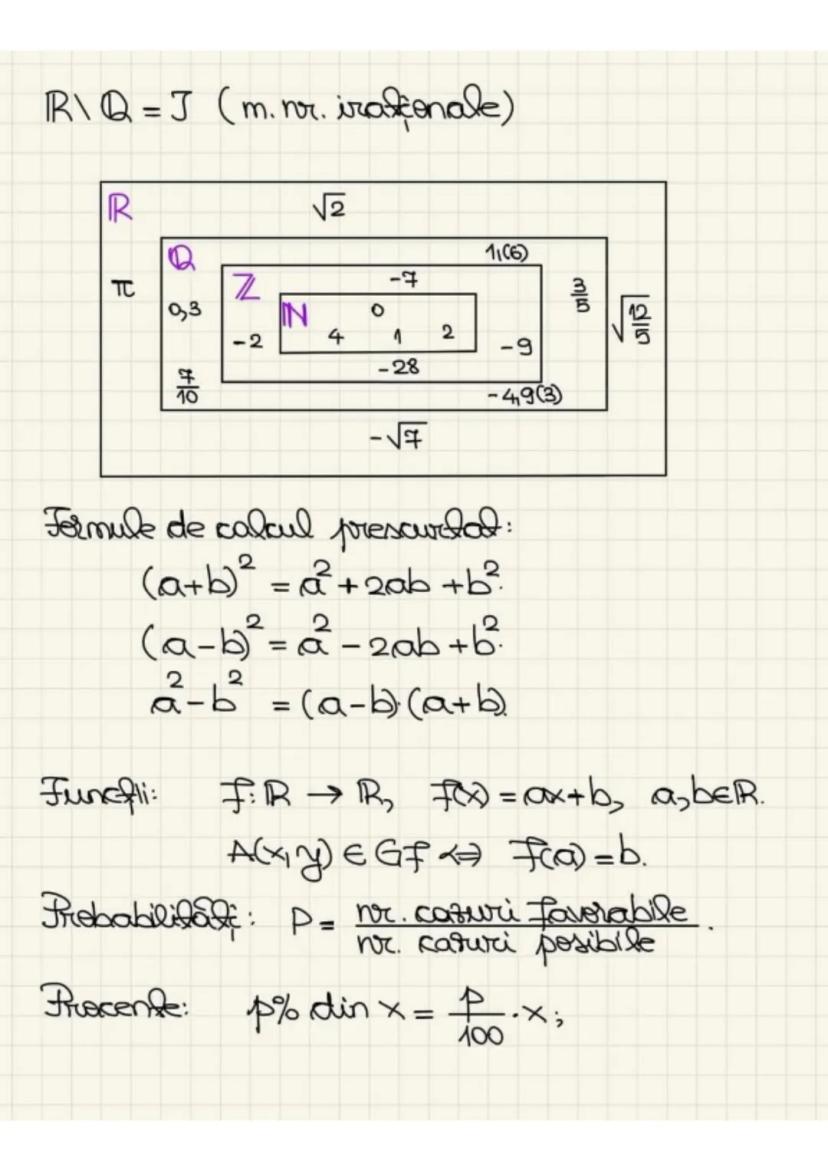
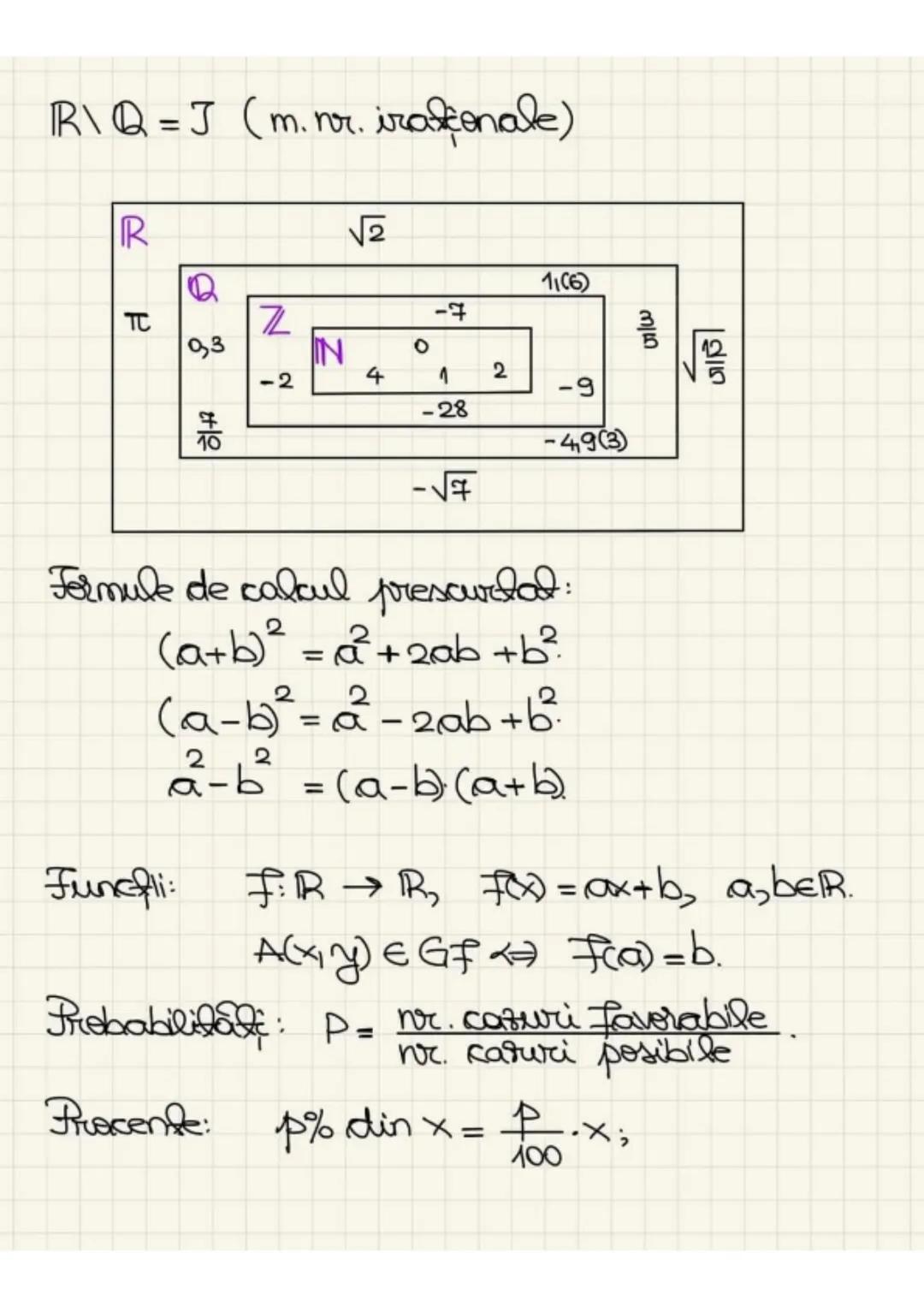
Mulțimea numerelor naturale este formată din $N = { 0, 1, 2, 3, ..... }$, iar mulțimea numerelor naturale nenule este $N^*= {1, 2, 3, 4, .....}$.

Când împărțim două numere, folosim teorema împărțirii cu rest: $D=T \times C+R$, unde R < T $Deîmpărțitul = Împărțitorul × Câtul + Restul$.

La operațiile cu puteri trebuie să ții minte regulile de bază:

• $a^m \cdot a^n = a^{m+n}$ (la înmulțire, aduni exponenții)
• $a^m : a^n = a^{m-n}$ (la împărțire, scazi exponenții)
• $(a^m)^n = a^{m \cdot n}$ (la ridicarea la putere, înmulțești exponenții)

💡 Reține că orice număr ridicat la puterea 0 este egal cu 1 (dacă numărul e diferit de 0), iar $(-1)$ ridicat la putere pară dă +1, iar la putere impară dă -1.

Operații cu mulțimi și proprietăți ale puterilor

Pentru puteri, mai reține că:

• $a^m \cdot b^m = (a \cdot b)^m$ (înmulțirea numerelor cu aceeași putere)
• $a^m : b^m = (a : b)^m$ (împărțirea numerelor cu aceeași putere)

Operațiile cu mulțimi sunt ușor de înțeles:

• Reuniunea $A \cup B$: toate elementele din ambele mulțimi, fără a repeta elementele comune
• Intersecția $A \cap B$: doar elementele comune ambelor mulțimi
• Diferența $A \setminus B$: elementele din A care nu se află și în B

Cardinalul unei mulțimi reprezintă numărul de elemente din mulțime. Vei folosi acest concept frecvent în probleme cu mulțimi.

💡 Nu uita că la reuniune includem elementele comune doar o singură dată, iar la diferență iei doar elementele care sunt exclusiv în prima mulțime!

Divizibilitate

Când spunem că "a se divide cu b", înseamnă că a se împarte exact la b, adică există un număr natural c astfel încât a = b × c. Notăm a:b.

Un număr prim este un număr natural care are exact doi divizori: 1 și el însuși. Divizorii 1 și numărul însuși se numesc divizori improprii, iar ceilalți sunt divizori proprii.

Criteriile de divizibilitate te ajută să verifici rapid dacă un număr se împarte exact cu altul:

• Cu 2: ultima cifră este pară (0, 2, 4, 6, 8)
• Cu 3: suma cifrelor este divizibilă cu 3
• Cu 5: ultima cifră este 0 sau 5
• Cu 9: suma cifrelor este divizibilă cu 9
• Cu 10: ultima cifră este 0

💡 Memorează bine criteriile de divizibilitate - îți vor economisi mult timp la testări și îți vor permite să verifici rapid rezultatele!

CMMDC, CMMMC și intervale de numere reale

Pentru a calcula cel mai mare divizor comun (CMMDC) a două numere:

• Descompui numerele în produse de factori primi
• Calculezi produsul factorilor primi comuni, luați o singură dată la puterea cea mai mică

Pentru cel mai mic multiplu comun (CMMMC):

• Descompui numerele în produse de factori primi
• Calculezi produsul factorilor primi comuni și necomuni, la puterea cea mai mare

Reține formula: CMMDC × CMMMC = a × b

Intervalele de numere reale pot fi mărginite sau nemărginite:

• [a,b] = numerele mai mari sau egale cu a și mai mici sau egale cu b
• [a,b) = numerele mai mari sau egale cu a și mai mici strict decât b
• (a,b] = numerele mai mari strict decât a și mai mici sau egale cu b
• (a,b) = numerele mai mari strict decât a și mai mici strict decât b

💡 O greșeală frecventă este confundarea parantezelor. Reține: paranteza rotundă înseamnă "strict", iar paranteza dreaptă include și capătul intervalului!

Mulțimea numerelor întregi și operații

Mulțimea numerelor întregi este: $Z=..., -3, -2, -1, 0, 1, 2, 3, ...$

• $Z+$ conține numerele întregi pozitive (1, 2, 3, ...)
• $Z-$ conține numerele întregi negative (..., -3, -2, -1)

La adunarea numerelor întregi cu semne diferite:

• Se păstrează semnul numărului cu valoare absolută mai mare
• Se face scăderea între valorile absolute

La adunarea numerelor cu același semn, valorile se adună și se păstrează semnul.

La înmulțire/împărțire:

• Dacă numerele au semne diferite, rezultatul este negativ
• Dacă numerele au același semn, rezultatul este pozitiv

💡 Nu te complica: la adunarea numerelor cu semne diferite, gândește-te ca la o "luptă" între valori - câștigă numărul mai mare și îți impune semnul său!

Mulțimea numerelor raționale și operații cu fracții

Mulțimea numerelor raționale ($Q$) este formată din toate fracțiile de forma $\frac{a}{b}$ unde a este un număr întreg și b este un număr întreg nenul.

Fracțiile pot fi:

• Supraunitare: când numărătorul > numitorul ex: $\frac{7}{3}$
• Echiunitare: când numărătorul = numitorul ex: $\frac{5}{5}$
• Subunitare: când numărătorul < numitorul ex: $\frac{2}{7}$

Pentru a introduce un număr întreg într-o fracție, folosești formula: $\frac{ab}{c} = \frac{a \cdot c + b}{c}$

La operații cu fracții, ține minte:

• Fracțiile se adună sau se scad doar dacă au același numitor
• La înmulțire: $\frac{a}{b} \times \frac{c}{d} = \frac{a \times c}{b \times d}$
• La împărțire: $\frac{a}{b} : \frac{c}{d} = \frac{a}{b} \times \frac{d}{c}$ (inversezi a doua fracție și înmulțești)

💡 Când vrei să aduni fracții cu numitori diferiți, nu uita să le aduci la același numitor - cel mai simplu este să folosești CMMMC al numitorilor!

Fracții zecimale, numere reale și radicali

Pentru fracții zecimale periodice, avem formulele:

• $\overline{a,b} = \frac{\overline{ab}}{10}$ (o zecimală periodică simplă)
• $\overline{a,(b)} = \frac{\overline{ab}-a}{9}$ (o zecimală periodică cu partea b)
• $\overline{a,b(c)} = \frac{\overline{abc}-\overline{ab}}{90}$ (zecimală periodică mixtă)

La operații cu radicali, reține regulile de bază:

• $\sqrt{a} \cdot \sqrt{b} = \sqrt{a \cdot b}$ (înmulțirea radicalilor)
• $\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}$ (împărțirea radicalilor)
• $a\sqrt{b} = \sqrt{a^2 \cdot b}$ (factorizarea din radical)

Atenție la proprietatea: $\sqrt{a^2} = |a|$ (valoarea absolută a lui a).

Valoarea absolută este definită astfel: $|a| = \begin{cases} a, a>0 \ -a, a<0 \end{cases}$

Media geometrică a două numere pozitive este: $m_g=\sqrt{a \cdot b}$

💡 La radicali, lucrează cu regulile de bază și nu uita că radical din pătratul unui număr este valoarea absolută a numărului, nu numărul însuși!

Formule de calcul și noțiuni suplimentare

Mulțimea numerelor reale (R) include toate tipurile de numere: naturale, întregi, raționale și iraționale. Numerele iraționale (I) sunt cele care nu pot fi scrise ca fracții și împreună cu numerele raționale (Q) formează mulțimea numerelor reale.

Formule de calcul prescurtat care te vor ajuta mult:

• $(a+b)^2 = a^2 + 2ab + b^2$ (pătratul unei sume)
• $(a-b)^2 = a^2 - 2ab + b^2$ (pătratul unei diferențe)
• $a^2 - b^2 = (a-b)(a+b)$ (diferența de pătrate)

O funcție este o relație care asociază fiecărui element x dintr-o mulțime un singur element y. Notăm f: R→R, f(x) = ax+b, unde a și b sunt numere reale.

Probabilitatea unui eveniment se calculează ca: P = $\frac{\text{număr cazuri favorabile}}{\text{număr cazuri posibile}}$

Pentru procente: p% din x = $\frac{p \cdot x}{100}$

💡 Formulele de calcul prescurtat sunt esențiale pentru algebra de nivel mediu. Învață-le bine și vei economisi mult timp la rezolvarea exercițiilor!