Aplicații ale Paralelismului în Plane
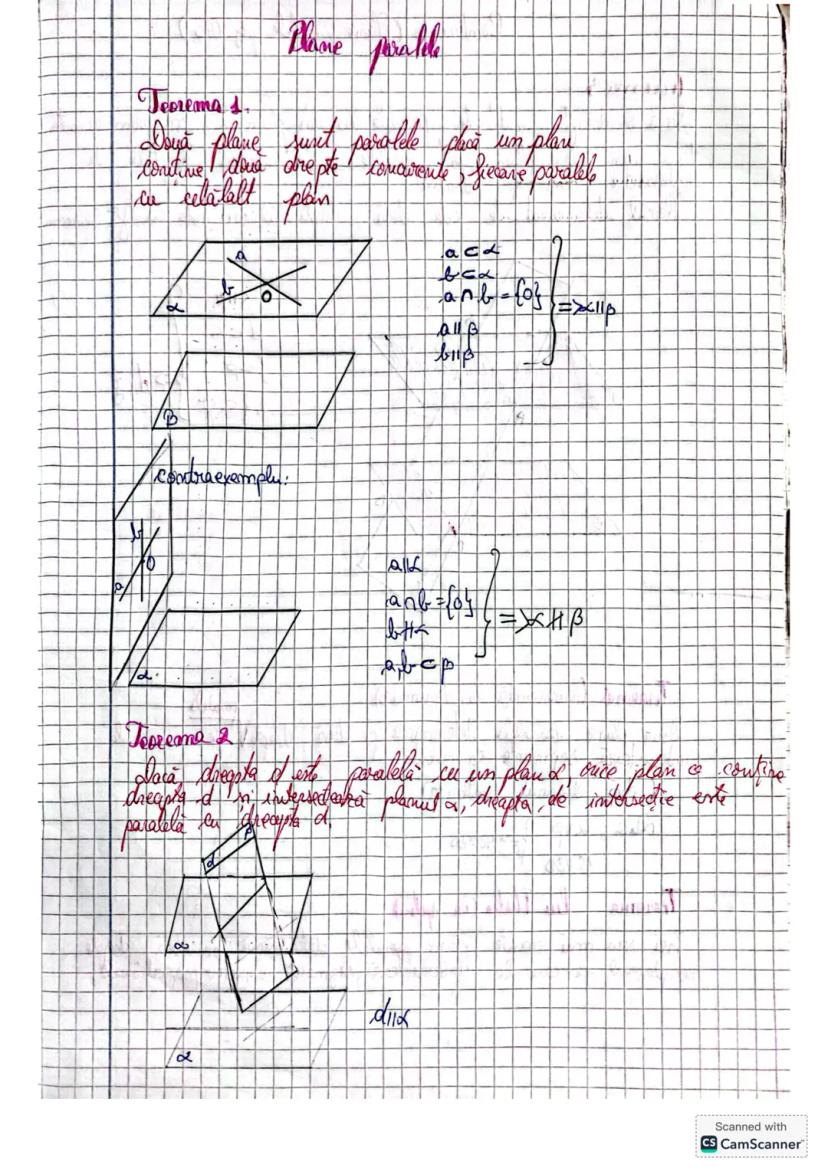
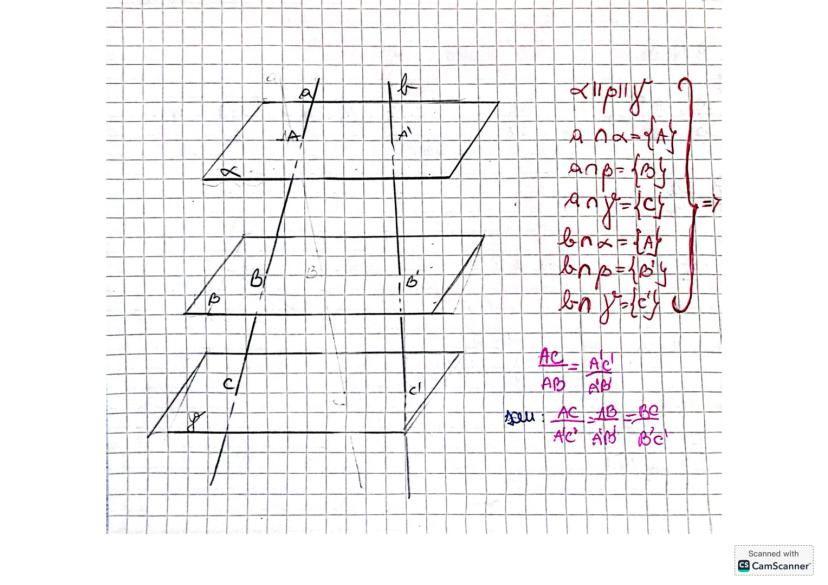
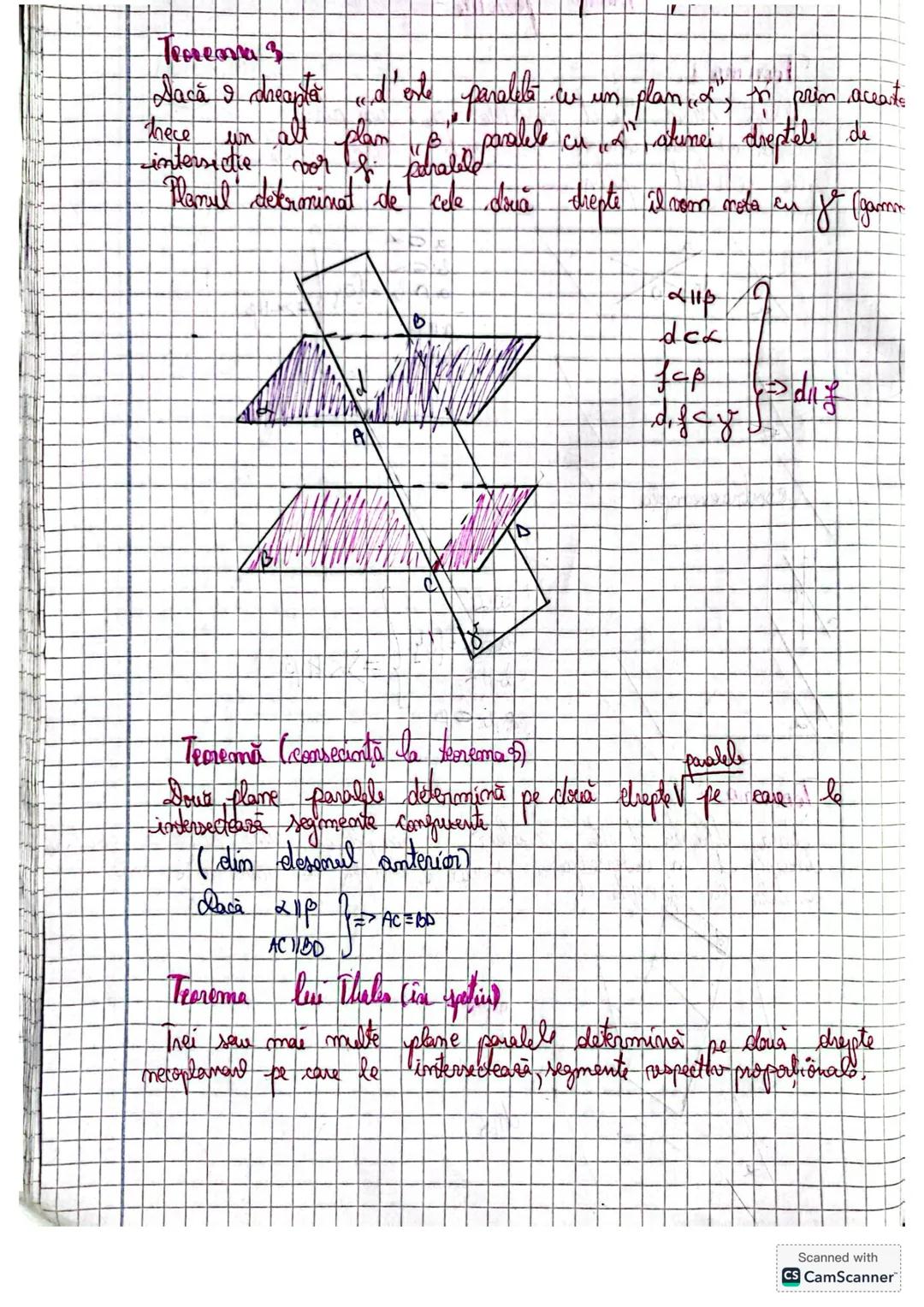
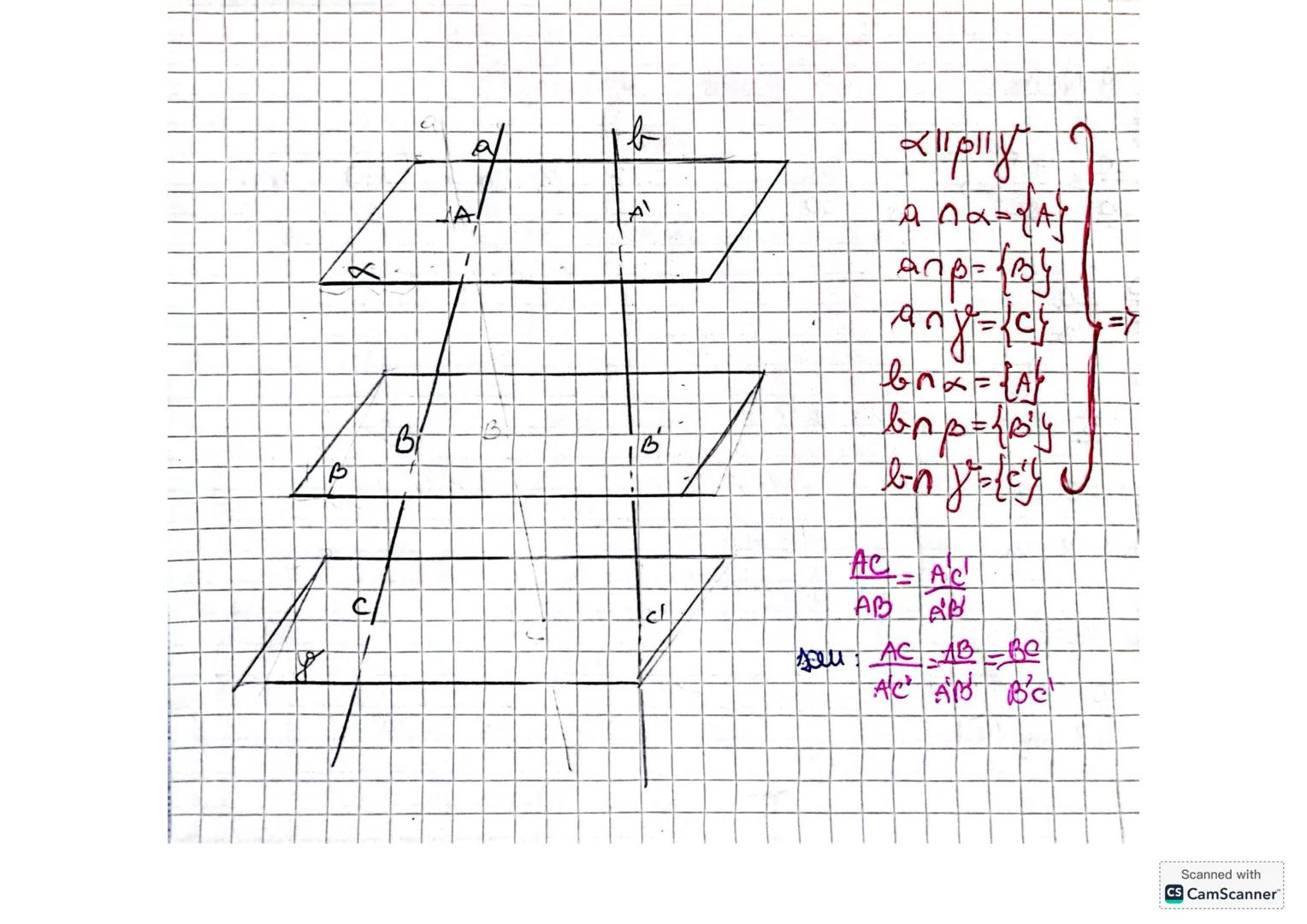
Când avem trei plane α, β și γ care se intersectează, se formează un sistem geometric interesant. Dacă dreapta a intersectează planul α în punctul A, și planul β în punctul B, iar o altă dreaptă b intersectează planul α tot în A și planul γ în punctul C, putem stabili relații importante.
În această configurație, putem analiza raportul dintre segmentele AC și AB, care ne ajută să stabilim relații de proporționalitate. Acest raport este esențial în demonstrarea unor teoreme avansate despre plane paralele.
Relația AC/AB este fundamentală și poate fi exprimată în funcție de pozițiile relative ale punctelor. Uneori, putem scrie această relație ca AC=M·AB sau putem demonstra că triunghiurile formate sunt asemenea.
💡 Util de știut: Aceste teoreme nu sunt doar abstracte - ele au aplicații practice în arhitectură, design 3D și în crearea modelelor matematice din lumea reală!