Introducere în Simularea Evaluării Naționale

Simularea Evaluării Naționale pentru clasa a VIII-a este un exercițiu important de pregătire pentru examenul real. Pe prima pagină găsești spațiile pentru datele tale personale și pentru notele evaluatorilor.

Testul are trei mari subiecte și durează două ore. Este important să completezi toate rubricile cu datele tale personale înainte de începerea testului.

Bine de știut: Poți obține 10 puncte din oficiu, chiar dacă nu rezolvi niciun exercițiu, dar ai șanse mult mai mari de succes dacă te pregătești temeinic!

Subiectul I - Exerciții cu alegere multiplă

Primul subiect conține șase exerciții, fiecare valorând 5 puncte. Trebuie doar să încercuiești litera corespunzătoare răspunsului corect din cele patru variante oferite.

Exercițiile testează cunoștințele tale de operații cu numere, fracții echivalente, procente, și probleme practice cum ar fi cea cu robinete care umplu un bazin.

La exercițiul 1 trebuie să calculezi expresia (2+2·2):2+2, respectând ordinea operațiilor. La exercițiul 4, dacă 10 robinete umplu un bazin în 6 ore, trebuie să afli în cât timp umplu 15 robinete același bazin.

Sfat util: La exercițiile cu alegere multiplă, verifică întotdeauna toate variantele de răspuns înainte să decizi, chiar dacă prima variantă îți pare corectă!

Subiectul I continuare și Subiectul al II-lea

Ultimele două exerciții din Subiectul I verifică operații cu mulțimi și numere iraționale. La exercițiul 5 trebuie să găsești intersecția mulțimilor A și B, iar la exercițiul 6 să verifici dacă 2√3 aparține intervalului (√12, √13).

Subiectul al II-lea se concentrează pe geometrie. Ai de rezolvat probleme despre:

• Drepte paralele și unghiuri
• Paralelogram și perimetru
• Cerc și aria triunghiului
• Distanțe în dreptunghi

La primul exercițiu trebuie să găsești valoarea lui x pentru ca două drepte să fie paralele, folosind unghiuri corespondente. La exercițiul 3, trebuie să calculezi aria triunghiului format de centrul cercului și o coardă.

Atenție: La geometrie, desenele sunt foarte importante! Analizează cu atenție figurile date și identifică toate informațiile relevante înainte de a încerca să rezolvi.

Subiectul al II-lea continuare și începutul Subiectului al III-lea

Ultimele două exerciții din Subiectul al II-lea sunt tot probleme de geometrie. La exercițiul 5 ai un dreptunghi cu mijloacele unor laturi marcate și trebuie să calculezi aria patrulaterului format. La exercițiul 6, într-un triunghi cu o paralelă la o latură, trebuie să determini suma x+y.

Subiectul al III-lea este diferit - aici trebuie să scrii rezolvările complete, nu doar să alegi un răspuns. Primul exercițiu este despre teoria numerelor - un număr natural care la împărțirea cu 3, 8 și 11 dă resturile 2, 7 și respectiv 10.

Trebuie să verifici dacă 527 îndeplinește aceste condiții și apoi să găsești cel mai mare număr de trei cifre care respectă condițiile. Vei folosi teorema împărțirii cu rest și poate teorema lui Bezout.

Sfat pentru rezolvare: La exercițiile cu divizibilitate, verifică pe rând fiecare condiție. Apoi, pentru a găsi numărul maxim, poți folosi congruențe sau metoda încercărilor succesive.

Subiectul al III-lea continuare

La exercițiul 2 ai de lucrat cu mulțimi și operații cu mulțimi. Trebuie să găsești elementele mulțimii A, unde fracția $3x+8$/$x+6$ trebuie să fie număr întreg, și elementele mulțimii B, care conține numere întregi cu valoarea absolută a lui x+3 mai mică sau egală cu 4.

După ce găsești elementele fiecărei mulțimi, trebuie să determini cardinalul intersecției lor, adică numărul de elemente comune. Pentru mulțimea A, trebuie să găsești valorile lui x pentru care numitorul nu divide numărătorul.

Pentru mulțimea B, trebuie să rezolvi inegalitatea |x+3|≤4, care înseamnă că x+3 este între -4 și 4, deci x este între -7 și 1.

Gândește-te așa: Pentru ca o fracție să dea un număr întreg, numitorul trebuie să dividă numărătorul, sau alternativ, x+6 trebuie să nu fie divizor al lui 3x+8 pentru elementele care NU sunt în mulțimea A.

Subiectul al III-lea continuare

La exercițiul 3 trebuie să lucrezi cu proporții. Ai proporția $7x+3y$/$5x+6y$=4/5 și trebuie să demonstrezi că 5x=3y și apoi să calculezi un alt raport.

Pentru a demonstra că 5x=3y, poți înmulți în cruce proporția, obținând 5$7x+3y$=4$5x+6y$, apoi să dezvolți și să grupezi termenii cu x și y. După ce simplifici, ar trebui să ajungi la relația cerută.

La punctul b, trebuie să folosești relația 5x=3y pentru a simplifica raportul $5x+8y$/$7x+9y$. Poți înlocui pe x cu 3y/5 în acest raport și apoi să simplifici.

Trucul matematic: La probleme cu proporții, înmulțirea în cruce este foarte utilă! Apoi grupează termenii similari pentru a observa relațiile ascunse între variabile.

Subiectul al III-lea continuare

Exercițiul 4 testează cunoștințele tale despre trapez dreptunghic. Ai un trapez ABCD cu dimensiunile date: AD=12√3m, BC=24m, CD=12m.

La punctul a, trebuie să demonstrezi că perimetrul trapezului este mai mic de 81m. Pentru aceasta, trebuie să calculezi și latura AB folosind teorema lui Pitagora sau alte proprietăți ale trapezului dreptunghic.

La punctul b, trebuie să calculezi aria triunghiului MAB, unde M este punctul de intersecție a diagonalelor AD și BC. Poți folosi formula ariei triunghiului folosind baza și înălțimea, sau alte formule precum cea cu semiprodusul.

Vizualizează geometric: În trapezul dreptunghic, unghiurile de la baza mare sunt drepte. Asta îți permite să folosești relații trigonometrice simple pentru a găsi dimensiunile necunoscute.

Subiectul al III-lea continuare

Exercițiul 5 te provoacă cu un triunghi echilateral MNP, unde punctul O este centrul unui cerc, NP este tangentă la cerc în punctul A, și AM=48 cm.

La punctul a, trebuie să determini perimetrul triunghiului MNP. Fiind un triunghi echilateral, toate laturile sunt egale, deci trebuie să găsești lungimea unei singure laturi și să o înmulțești cu 3.

La punctul b, trebuie să demonstrezi că sinusul unghiului NOP este 4√3/7. Pentru asta, poți folosi relații trigonometrice în triunghiuri. Poți forma un triunghi dreptunghic și să calculezi sinusul folosind raportul dintre cateta opusă și ipotenuză.

Reține: Într-un triunghi echilateral, toate laturile sunt egale și toate unghiurile sunt de 60°. Aceste proprietăți îți simplifică mult calculele!

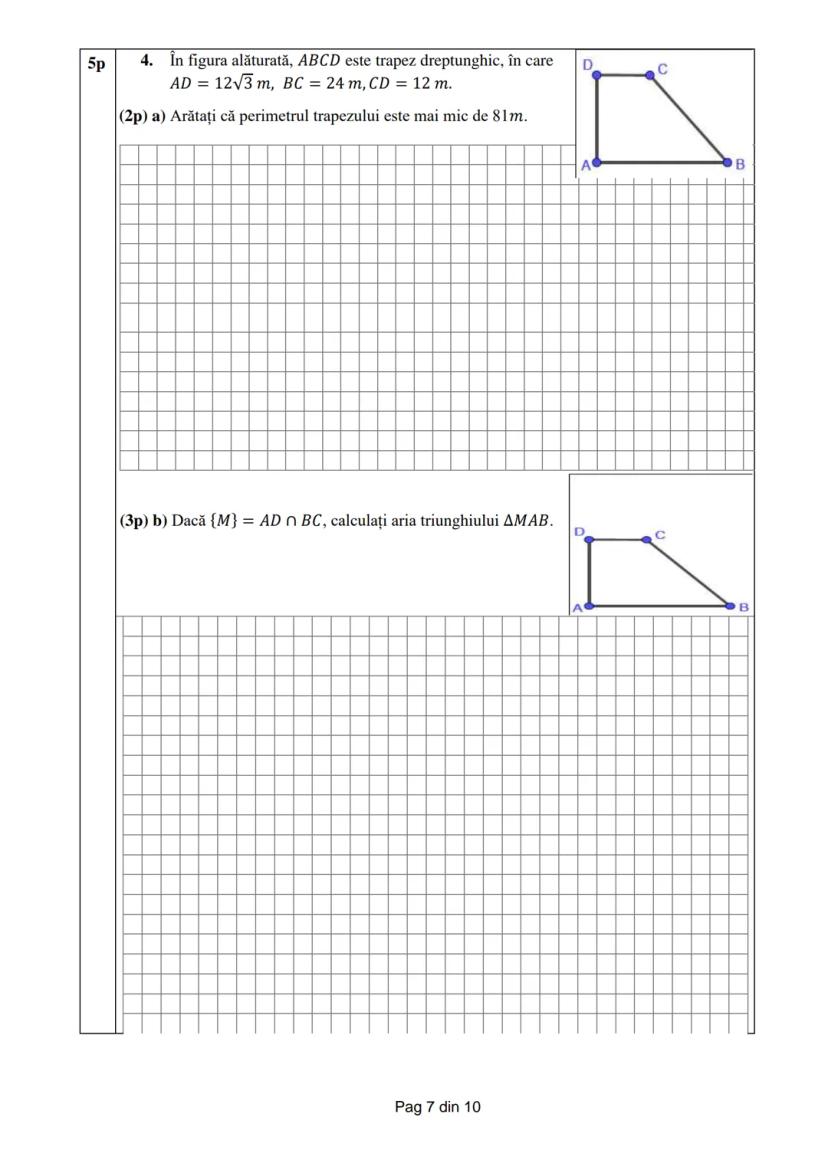
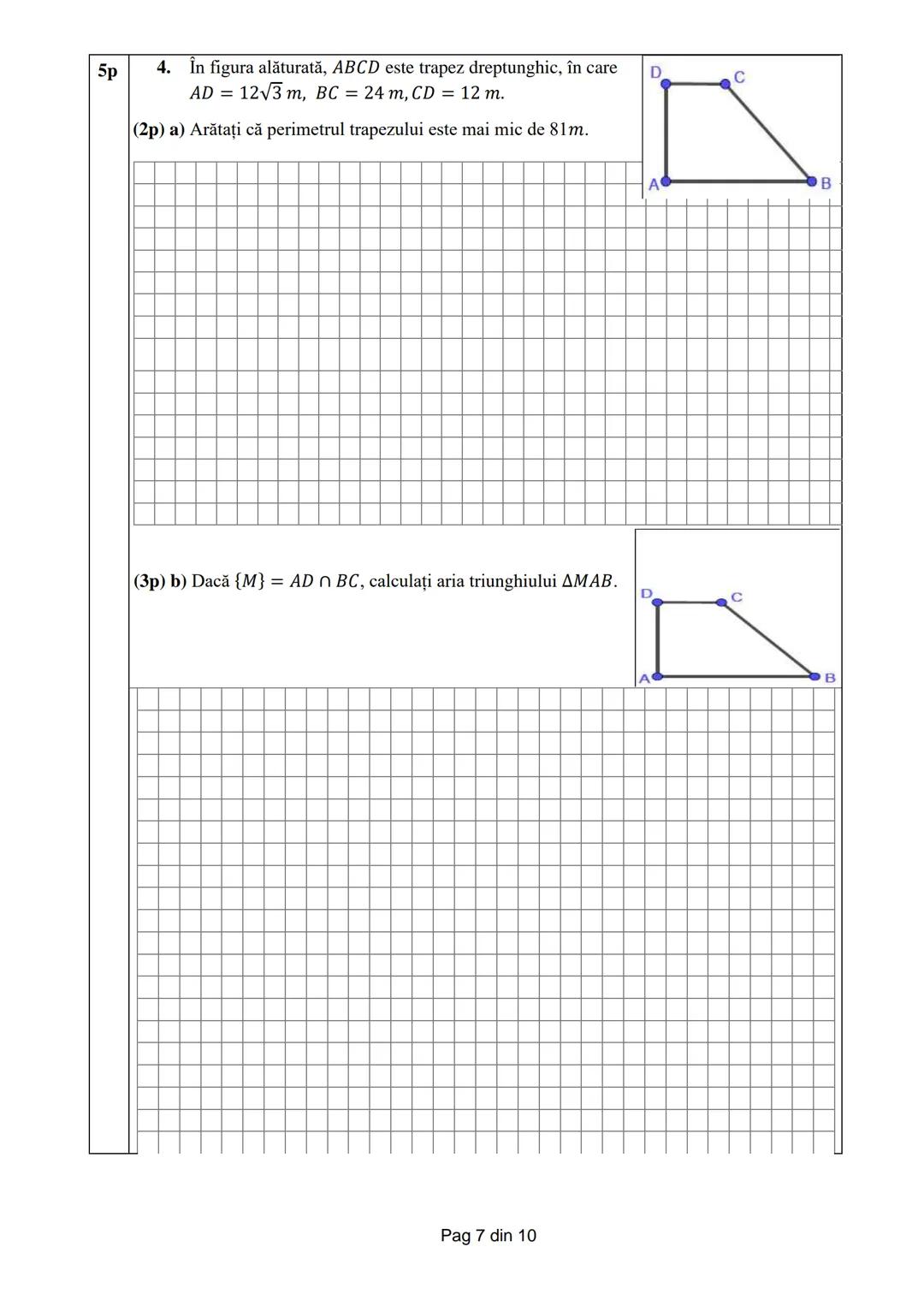
Subiectul al III-lea final

Ultimul exercițiu te provoacă cu geometria în spațiu, mai exact un cub ABCDA'B'C'D'. Punctele M, N, P, Q sunt mijloacele muchiilor AA', AD, B'C' și respectiv CC'.

La punctul a, trebuie să demonstrezi că MN este paralelă cu PQ. Pentru aceasta, poți folosi vectori sau coordonate în spațiu. Dacă două drepte au aceeași direcție (vectorii directori sunt coliniari), atunci dreptele sunt paralele.

La punctul b, trebuie să calculezi măsura unghiului dintre MN și BC. Poți folosi produsul scalar al vectorilor pentru a găsi cosinusul unghiului, apoi să deduci unghiul propriu-zis.

Imaginează-ți spațial: În problemele cu cuburi, este util să introduci un sistem de coordonate cu originea într-un vârf și axele de-a lungul muchiilor. Astfel, fiecare vârf va avea coordonate formate doar din 0 și 1.

Recapitulare și sfaturi pentru Evaluarea Națională

Această simulare acoperă toate tipurile de probleme pe care le vei întâlni la examenul real. Iată câteva sfaturi pentru succes:

1. Începe cu exercițiile care ți se par mai ușoare pentru a acumula puncte rapid.
2. La exercițiile cu alegere multiplă, elimină mai întâi variantele evident greșite.
3. La geometrie, fă desene clare și marchează toate informațiile date.

Verifică-ți calculele de două ori și nu uita să justifici toate pașii la Subiectul al III-lea. Ai la dispoziție două ore, deci organizează-ți bine timpul.

Încredere maximă: Dacă te-ai descurcat bine la această simulare, ești pe drumul cel bun pentru examenul real! Continuă să exersezi și să rezolvi probleme similare.