Determinarea dreptei și a planului

Ai observat vreodată că ai nevoie de două puncte ca să trasezi o linie? Două puncte diferite determină întotdeauna o singură dreaptă. Asta înseamnă că dacă ai punctele A și B, există o singură dreaptă AB care trece prin ele.

Pentru a determina un plan, avem nevoie de mai multe elemente. Trei puncte necoliniare (care nu se află pe aceeași dreaptă) determină întotdeauna un singur plan. Imaginează-ți trei picioare ale unui scaun - ele vor stabili mereu un plan unic.

💡 Sfat util: Când lucrezi cu probleme de geometrie în spațiu, desenează mereu un punct diferit față de celelalte (nu coliniare). Aceasta este cea mai simplă metodă de a obține un plan.

Teoreme de determinare a planului

O altă modalitate de a determina un plan este prin două drepte paralele. Când ai două linii paralele, există un singur plan care le conține pe ambele. Gândește-te la șinele de cale ferată - ele determină un plan unic.

Pentru a demonstra asta, folosim axioma paralelelor. Dacă avem drepte paralele a și b, iar A este un punct pe a, atunci există o singură dreaptă prin A care este paralelă cu b. Combinând aceste informații, obținem un plan unic.

În aplicații practice, putem folosi aceste teoreme pentru a identifica toate planele și dreptele determinate de puncte date. De exemplu, într-un paralelipiped drept ABCDEFGH, putem identifica toate dreptele ce conțin muchiile și toate planele determinate de câte două drepte paralele.

💡 Reține: Un paralelipiped cu 8 vârfuri are 12 muchii (drepte) și 6 fețe (plane). Poți folosi aceste informații pentru a rezolva rapid probleme legate de aceste corpuri.

Tetraedrul, piramida și prisma

Tetraedrul este corpul geometric format din 4 puncte necoplanare. E ca și cum ai construi un cort din patru bețe care se întâlnesc în patru puncte diferite.

Piramida este un corp determinat de un poligon (numit bază) și un punct care nu se află în planul poligonului (numit vârful piramidei). Într-o piramidă distingem:

• Baza (poligonul de jos)
• Vârful (punctul de sus)
• Muchii laterale (segmentele care unesc vârful cu vârfurile bazei)
• Muchiile bazei (laturile poligonului)
• Fețe laterale (triunghiurile formate de vârf și laturile bazei)

După forma bazei, piramidele pot fi triunghiulare, patrulatere, hexagonale etc. Tetraedrele sunt de fapt piramide triunghiulare, dar la un tetraedru oricare dintre fețe poate fi considerată bază.

💡 Interesant: Un tetraedru are 4 fețe, toate triunghiulare. Poți să-l privești din orice parte și tot tetraedru rămâne!

Piramide regulate și tetraedre

O piramidă este regulată când baza este un poligon regulat, iar înălțimea cade în centrul cercului circumscris bazei. Asta înseamnă că vârful piramidei se află exact deasupra centrului bazei.

În piramidele regulate:

• Toate muchiile laterale sunt congruente (au aceeași lungime)
• Toate fețele laterale sunt triunghiuri isoscele congruente

Apotema piramidei este înălțimea unei fețe laterale trasată din vârful piramidei. Este ca distanța de la vârful piramidei până la mijlocul unei laturi a bazei, măsurată pe fața laterală.

Piramidele pot avea diferite tipuri de baze regulate: triunghiulară (triunghi echilateral), patrulateră (pătrat), hexagonală (hexagon regulat).

Tetraedrul regulat este un tip special de piramidă unde toate cele șase muchii sunt congruente. Imaginează-ți un "cort" perfect simetric, unde toate laturile au aceeași lungime.

💡 Aplicație practică: Apotema piramidei este utilă pentru calculul ariei fețelor laterale. Înmulțește-o cu jumătate din perimetrul bazei pentru a obține aria laterală totală.

Pozițiile relative a două drepte în spațiu

În geometria plană, două drepte pot fi doar paralele sau concurente. În spațiu, situația e mai complexă! Două drepte pot fi:

1. Coplanare - situate în același plan:

   • Paralele (nu au niciun punct comun)
   • Concurente $se intersectează într-un punct$

2. Necoplanare - nu sunt situate în același plan și nu se intersectează niciodată.

Când te uiți la pozițiile unei drepte față de un plan, ai trei posibilități:

1. Dreaptă inclusă în plan - când dreapta și planul au cel puțin două puncte comune. Practic, dreapta se află complet în plan.

💡 Vizualizare simplă: Gândește-te la dreaptele necoplanare ca la două creioane în spațiu care nu se ating și nu sunt paralele. Nu există un singur plan care să le conțină pe ambele!

Poziții relative între drepte și plane

Pe lângă dreapta inclusă în plan, mai avem două poziții posibile:

2. Dreaptă secantă la plan - când dreapta și planul au exact un punct comun. Imaginează-ți un creion care înțeapă o foaie de hârtie - punctul de intersecție este unic.

3. Dreaptă paralelă cu planul - când dreapta și planul nu au niciun punct comun. Gândește-te la o linie trasă în aer deasupra unei mese.

Există o teoremă importantă despre paralelismul dintre o dreaptă și un plan: Dacă o dreaptă necuprinsă într-un plan este paralelă cu o dreaptă situată în plan, atunci ea este paralelă cu planul.

De asemenea, în spațiu există tranzitivitatea paralelismului: două drepte diferite paralele cu o a treia dreaptă nu sunt neapărat paralele între ele (spre deosebire de geometria plană)!

💡 Sfat practic: Pentru a verifica dacă o dreaptă este paralelă cu un plan, caută o dreaptă din plan paralelă cu dreapta dată. Dacă găsești una, atunci dreapta și planul sunt paralele.

Unghiuri între drepte în spațiu

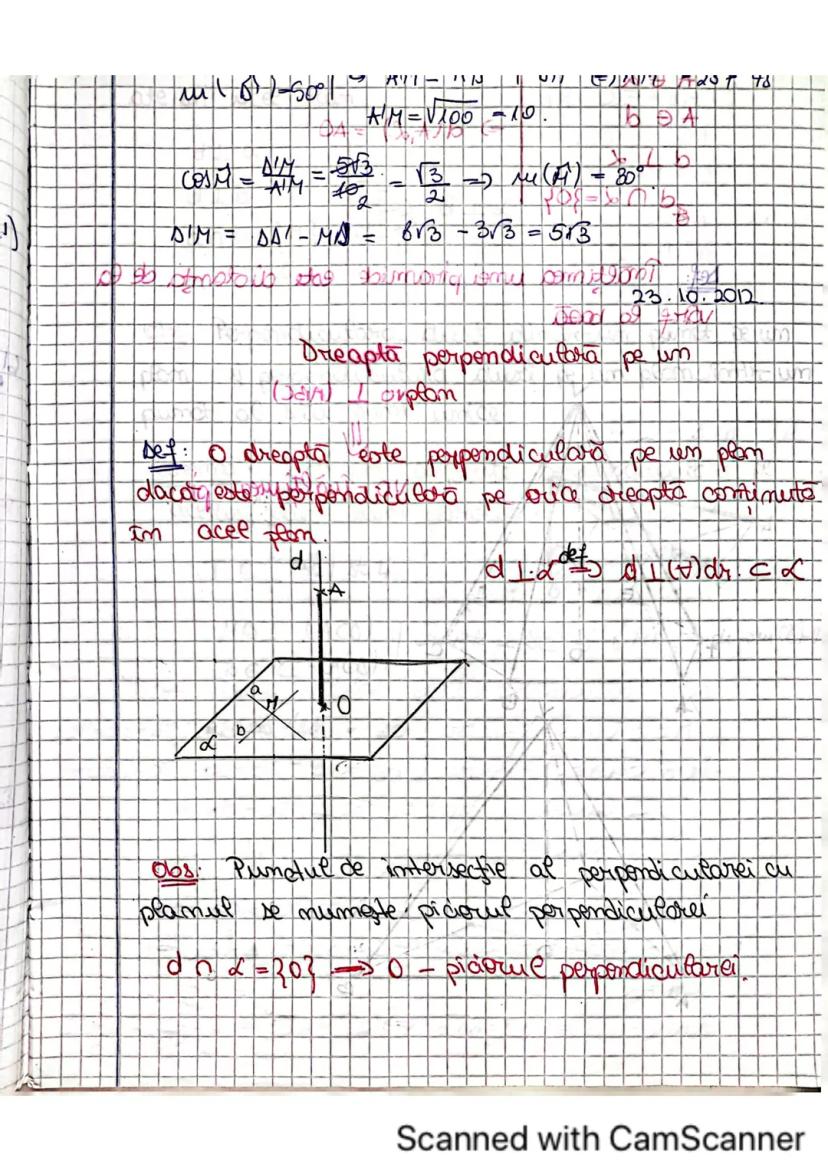
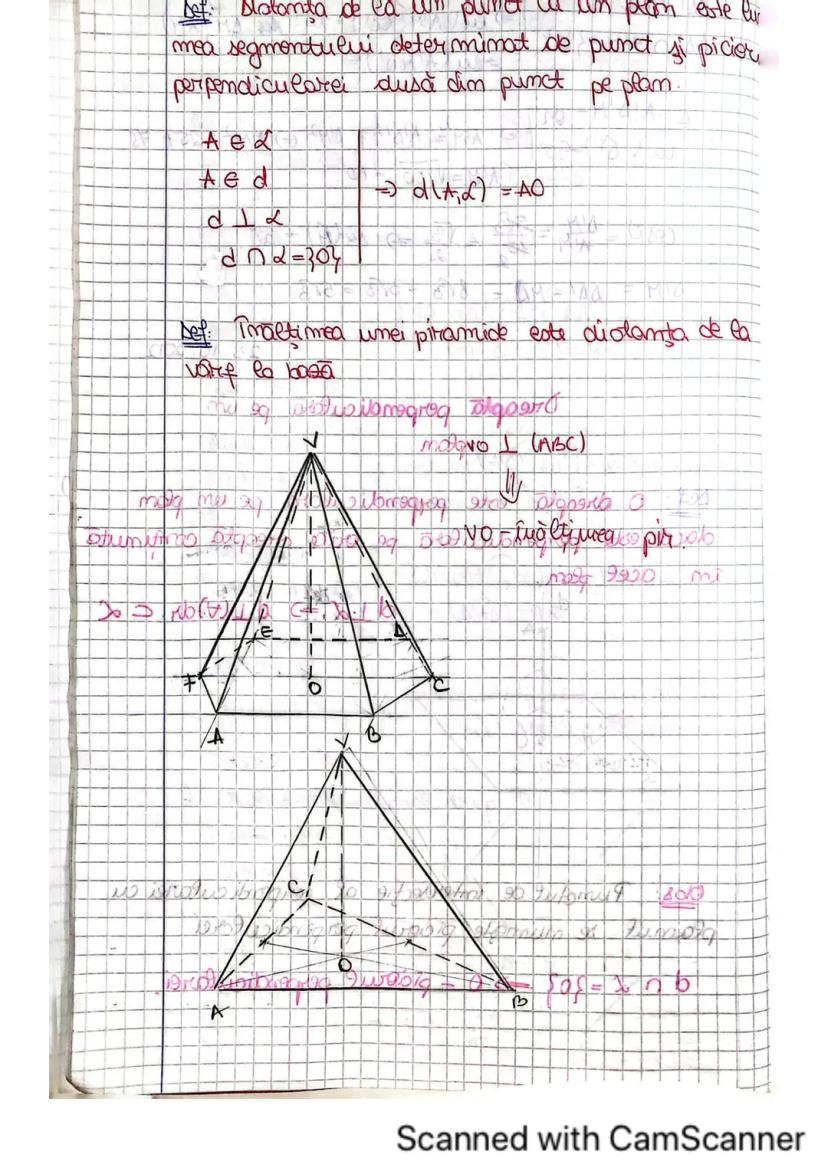
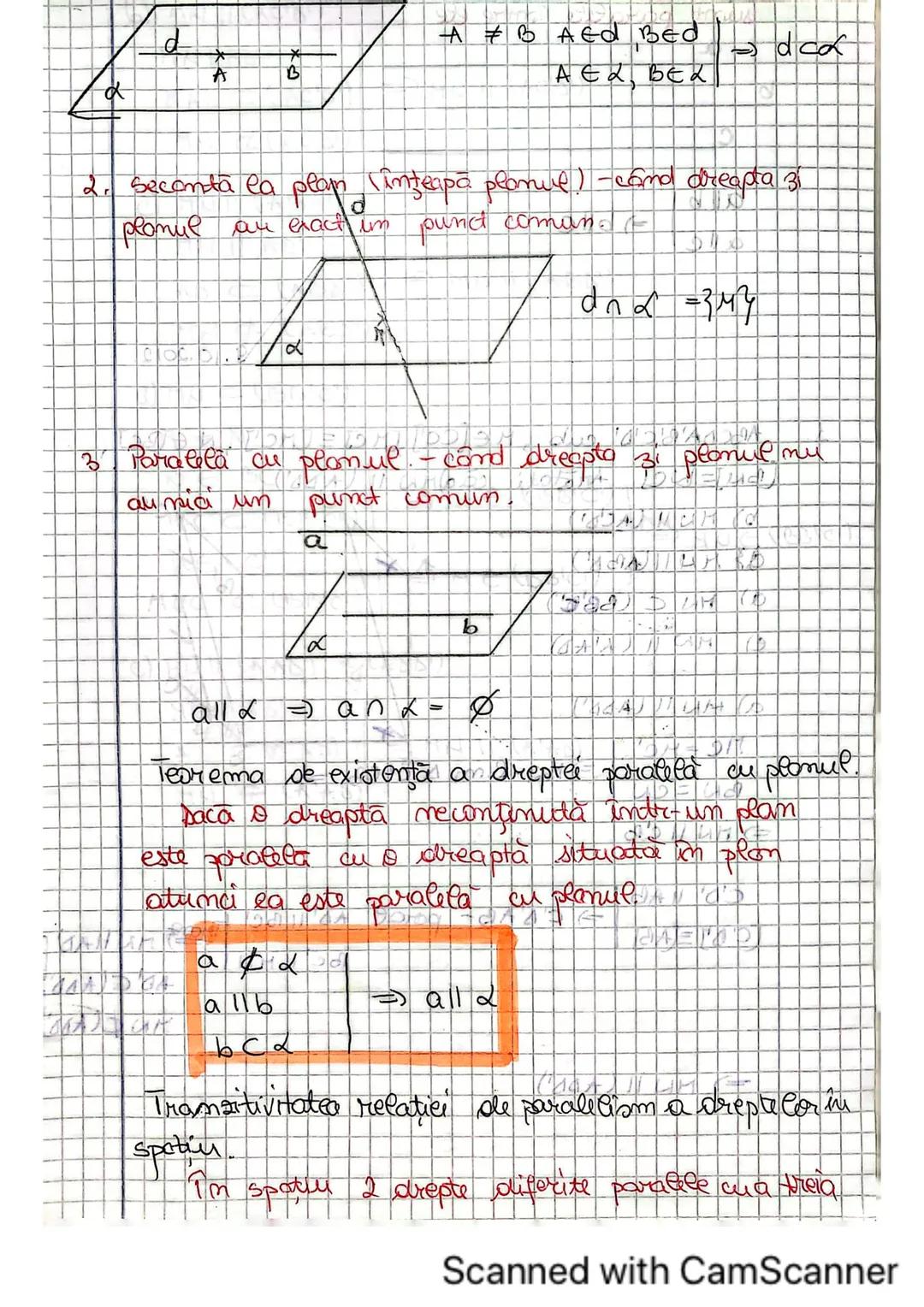
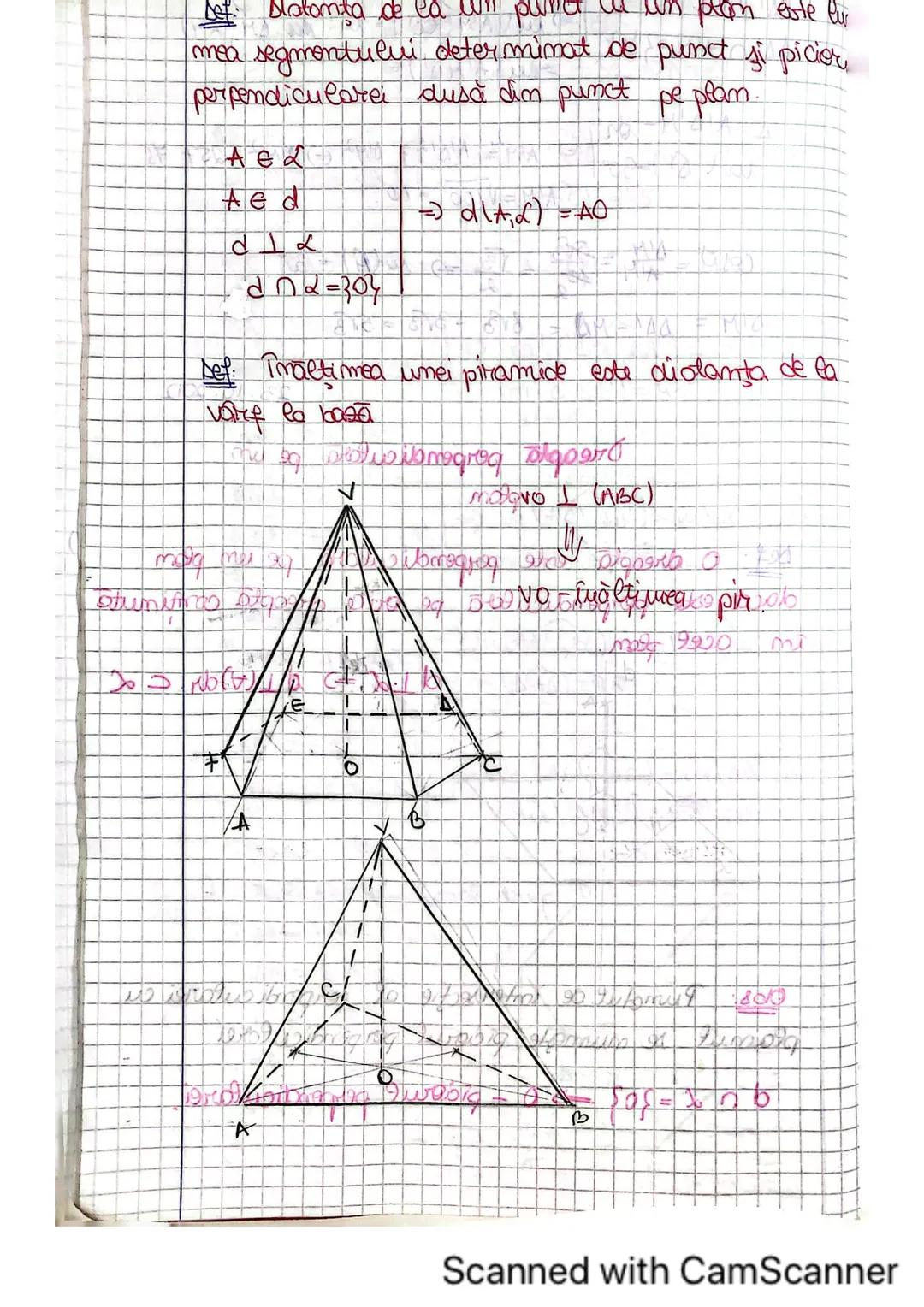
Cum măsurăm unghiul între două drepte care nu se intersectează? Unghiul a două drepte necoplanare în spațiu este unghiul ascuțit sau drept format între una din drepte și o paralelă la cealaltă dreaptă, dusă printr-un punct al primei drepte.

Cu alte cuvinte, "aducem" una din drepte lângă cealaltă prin intermediul unei paralele, apoi măsurăm unghiul format. Dacă acest unghi măsoară 90°, atunci dreptele sunt perpendiculare în spațiu.

Un principiu important: două unghiuri cu laturile respectiv paralele sunt congruente (dacă ambele sunt ascuțite sau ambele obtuze) sau sunt suplementare (dacă unul este ascuțit și celălalt obtuz).

Această proprietate ne ajută să comparăm unghiuri în configurații spațiale complexe, simplificând multe probleme de geometrie în spațiu.

💡 Aplicație: În arhitectură, această metodă este folosită pentru a măsura unghiurile dintre grinzi care nu se intersectează direct, dar care trebuie să respecte anumite condiții de perpendicularitate sau paralelism.

Dreapta perpendiculară pe un plan

O dreaptă este perpendiculară pe un plan dacă este perpendiculară pe orice dreaptă conținută în acel plan. Imaginează-ți un stâlp perfect vertical pe pământ - el este perpendicular pe orice direcție ai merge pe pământ.

Punctul de intersecție al perpendicularei cu planul se numește piciorul perpendicularei. Acest punct este unic pentru fiecare perpendiculară.

Distanța de la un punct la un plan este lungimea segmentului determinat de punct și piciorul perpendicularei dusă din punct pe plan. Este cea mai scurtă distanță dintre punct și plan.

Un exemplu practic este înălțimea unei piramide, care reprezintă distanța de la vârf la bază (planul bazei). Este segmentul perpendicular de la vârf la bază.

💡 Vizualizare: Gândește-te la o perpendiculară pe plan ca la umbra unui stâlp la amiază când soarele este exact deasupra. Umbra este un punct, iar stâlpul este perpendicular pe sol.

Distanțe în geometria spațiului

Distanța de la un punct A la un plan α este lungimea segmentului AO, unde O este piciorul perpendicularei dusă din A pe planul α. Este cel mai scurt drum de la punct la plan.

În cazul piramidelor, înălțimea reprezintă distanța de la vârf la baza piramidei. Aceasta este perpendiculară pe planul bazei și ne ajută la calcularea volumului piramidei.

O altă noțiune importantă este apotema bazei - distanța de la centrul bazei la una dintre laturile bazei, măsurată perpendicular pe acea latură.

În piramidele regulate, apotema piramidei și apotema bazei sunt elemente esențiale pentru calcularea ariei laterale și a volumului.

💡 Formulă utilă: Volumul piramidei = (1/3) × Aria bazei × Înălțimea. Reține această formulă pentru a rezolva rapid probleme cu piramide!

Teoreme despre perpendicularitate

Există o teoremă importantă despre existența dreptei perpendiculare pe plan: O dreaptă este perpendiculară pe un plan dacă este perpendiculară pe două drepte concurente situate în acel plan.

Această teoremă ne oferă o metodă practică de a verifica dacă o dreaptă este perpendiculară pe un plan - trebuie doar să demonstrăm că este perpendiculară pe două drepte din plan care se intersectează.

Observații importante:

• Perpendiculara dusă dintr-un punct pe un plan este unică
• Perpendiculara dusă pe un plan într-un punct al său este unică
• Două drepte diferite perpendiculare pe același plan sunt paralele

Aceste proprietăți sunt esențiale pentru rezolvarea problemelor de geometrie în spațiu și pentru construcția unor structuri în lumea reală.

💡 Aplicație practică: În construcții, această teoremă este folosită pentru a verifica dacă un stâlp este perfect vertical (perpendicular) pe sol. Constructorii măsoară perpendicularitatea față de două direcții diferite din planul solului.