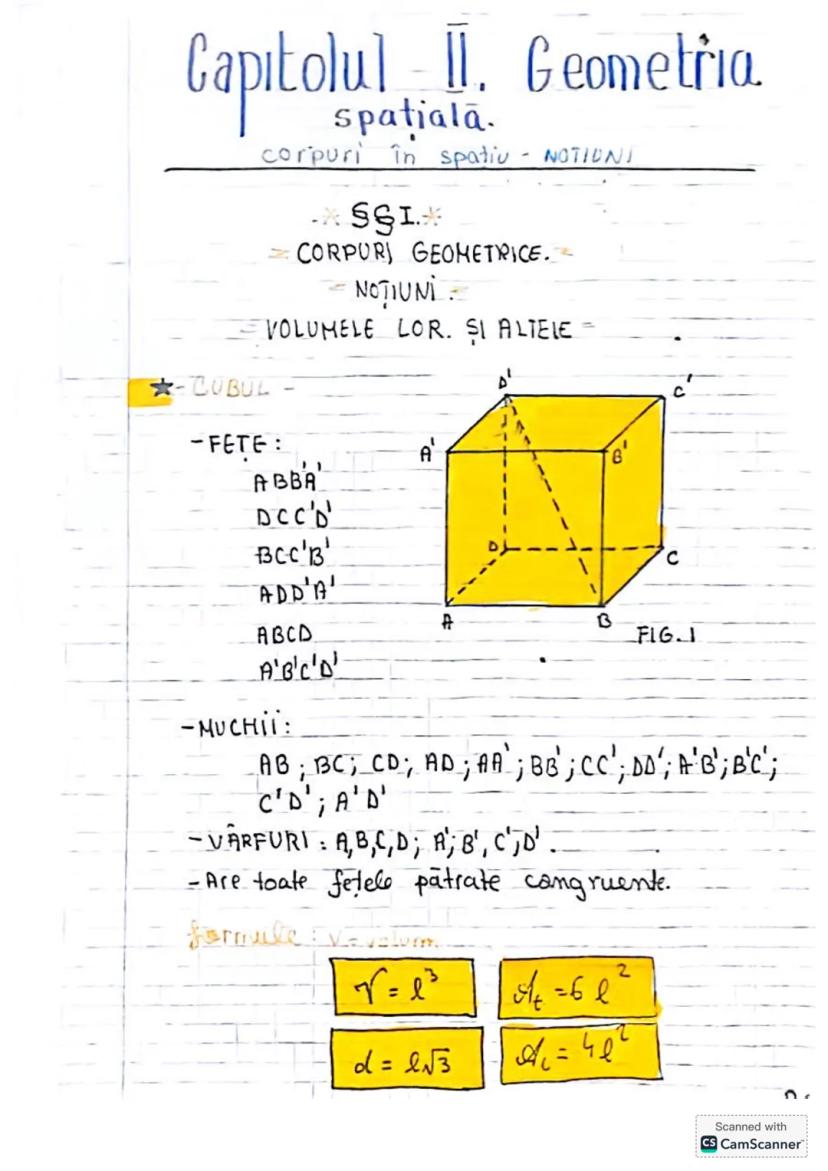
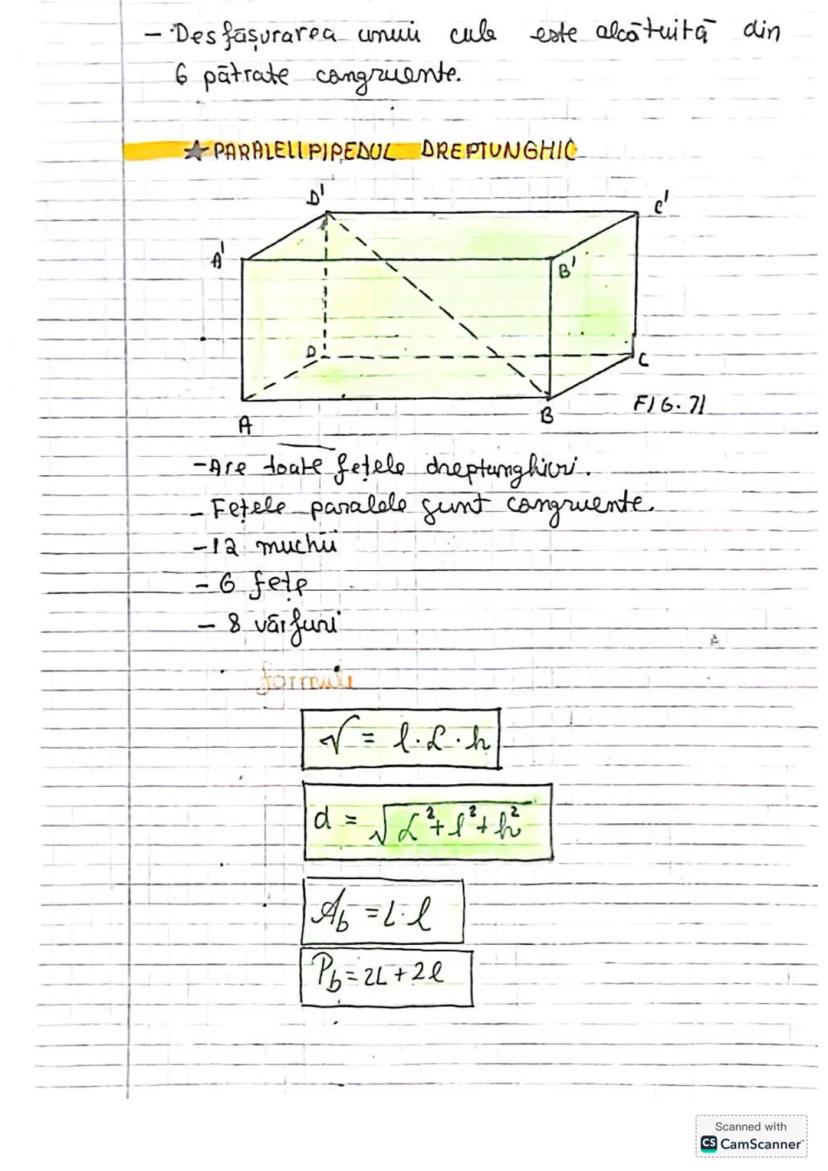
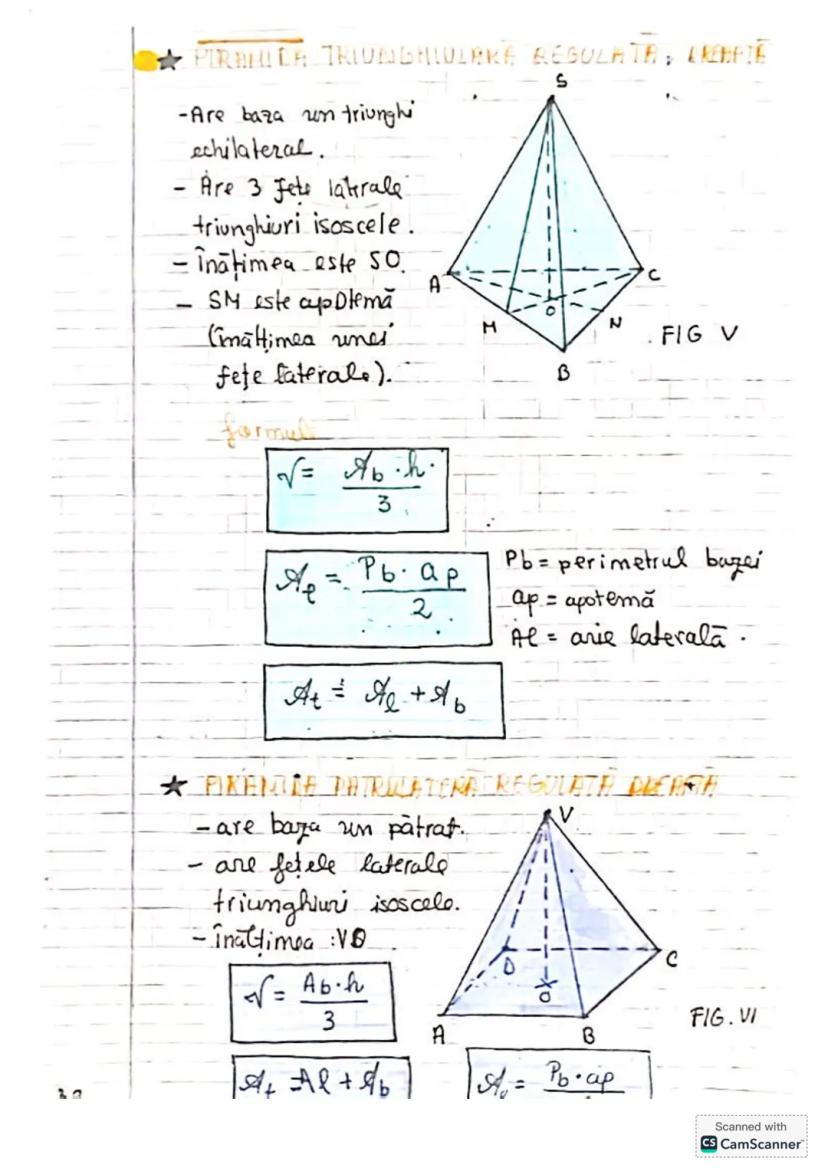
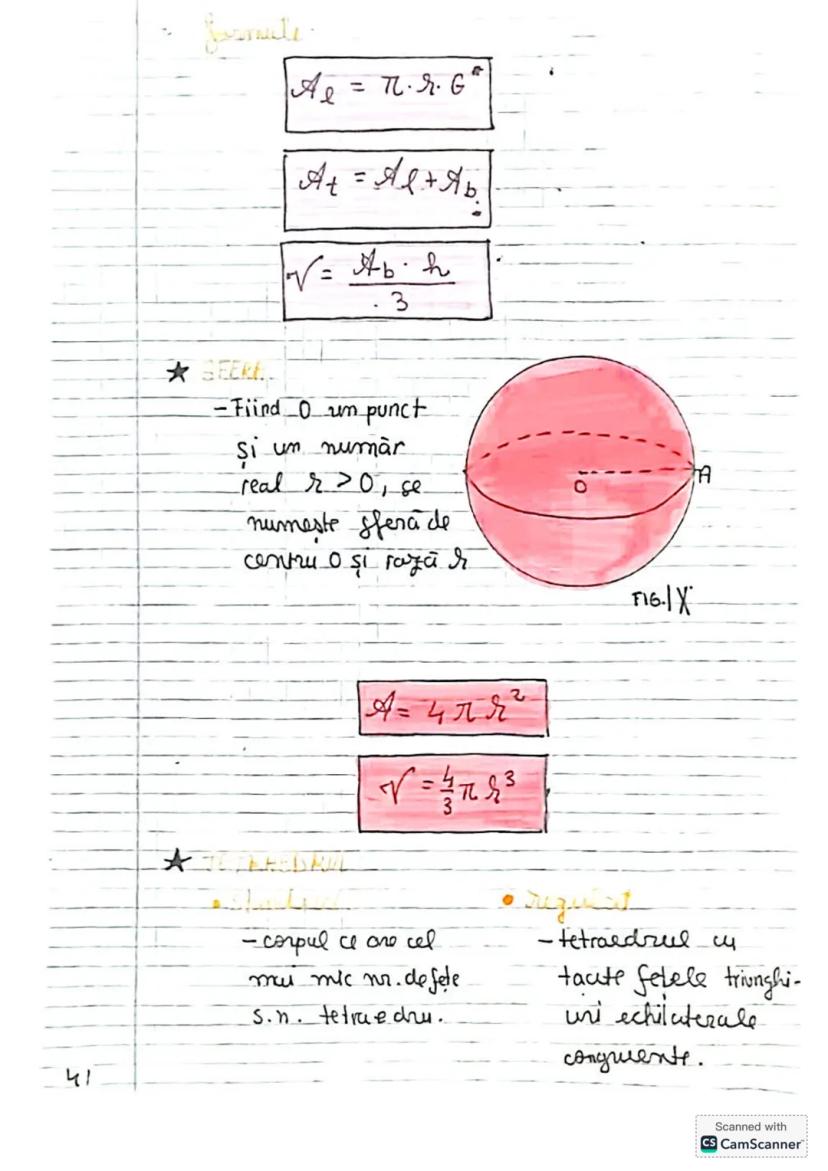
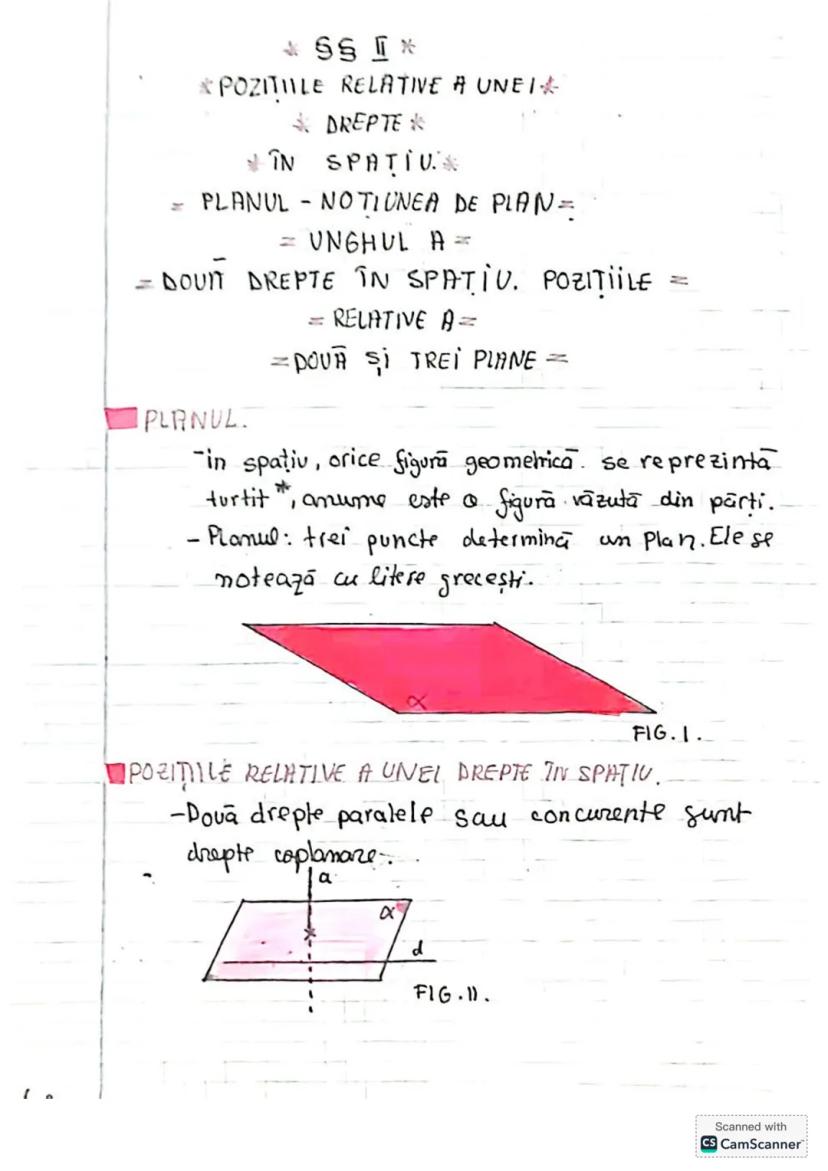
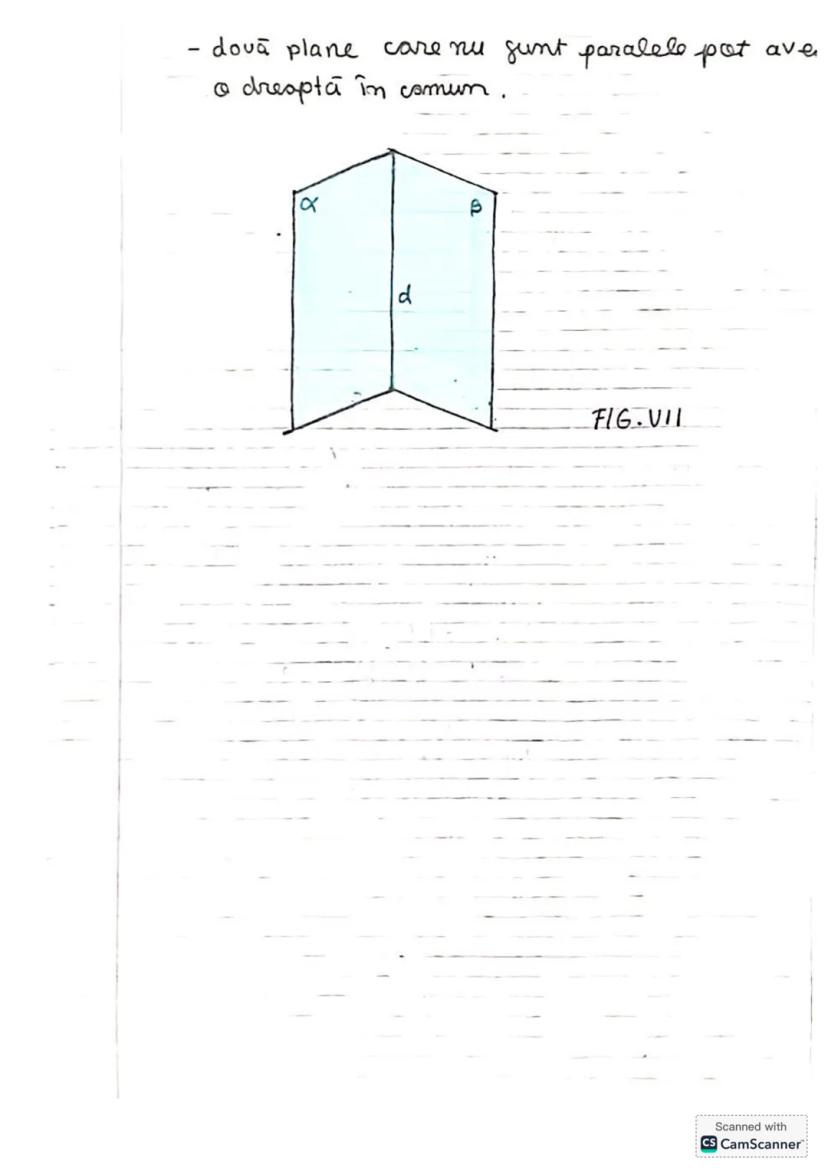
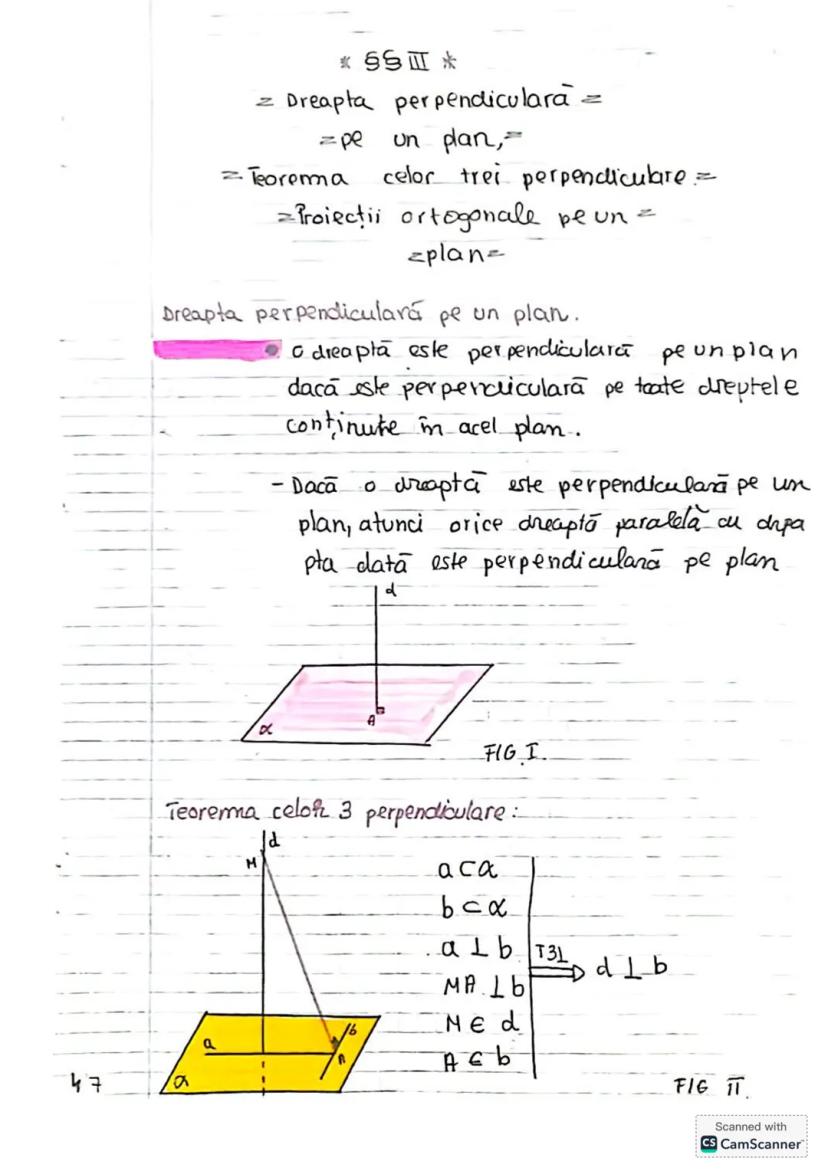
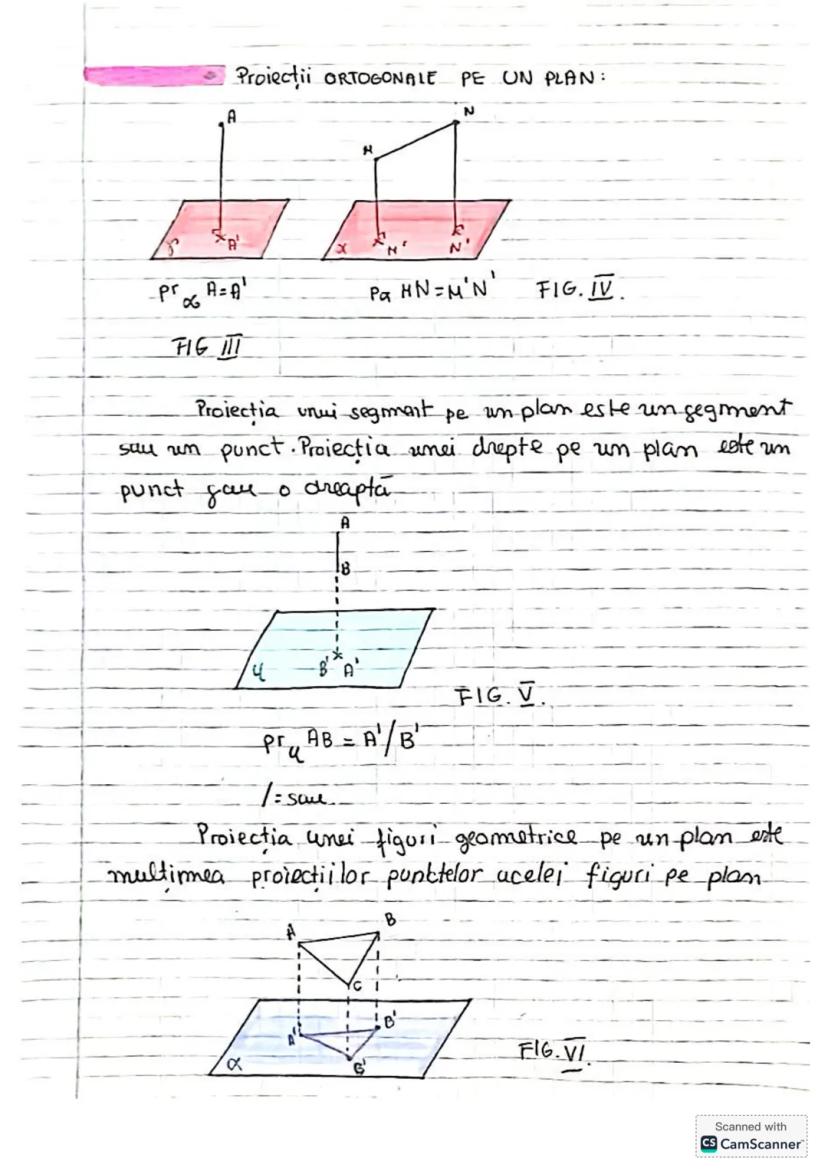
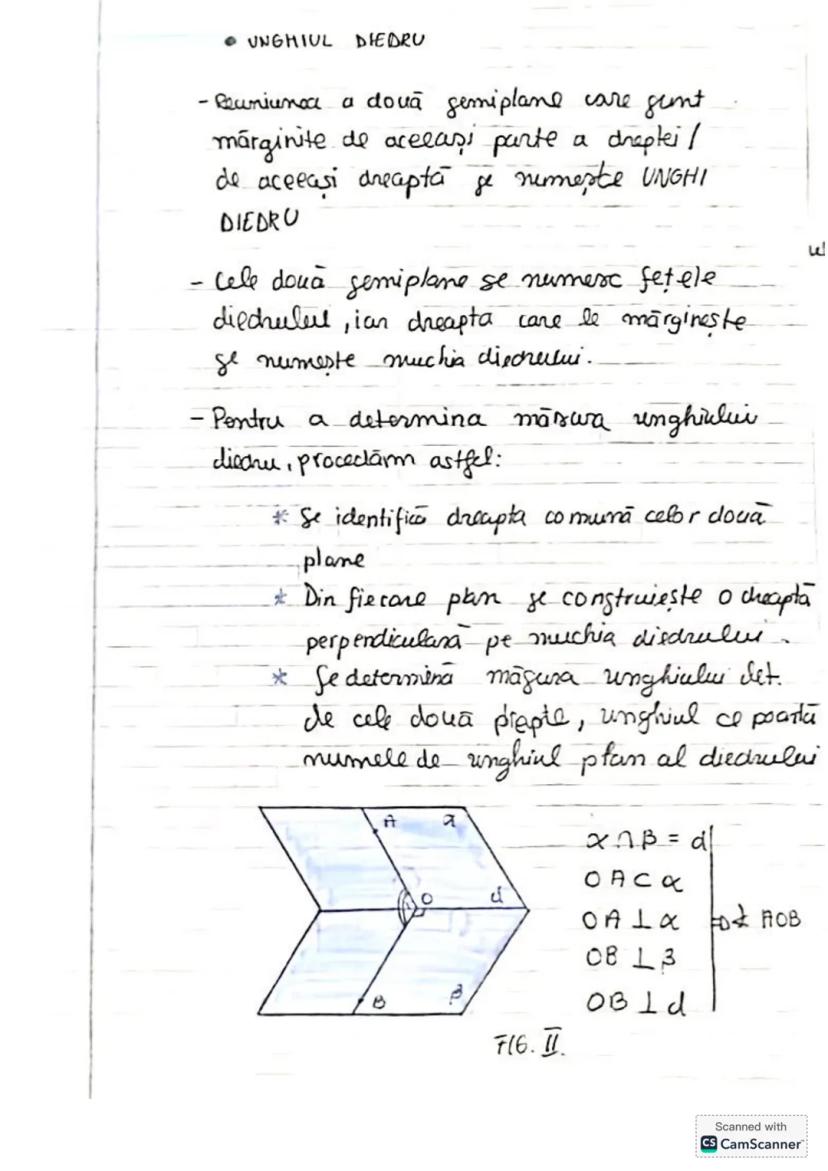
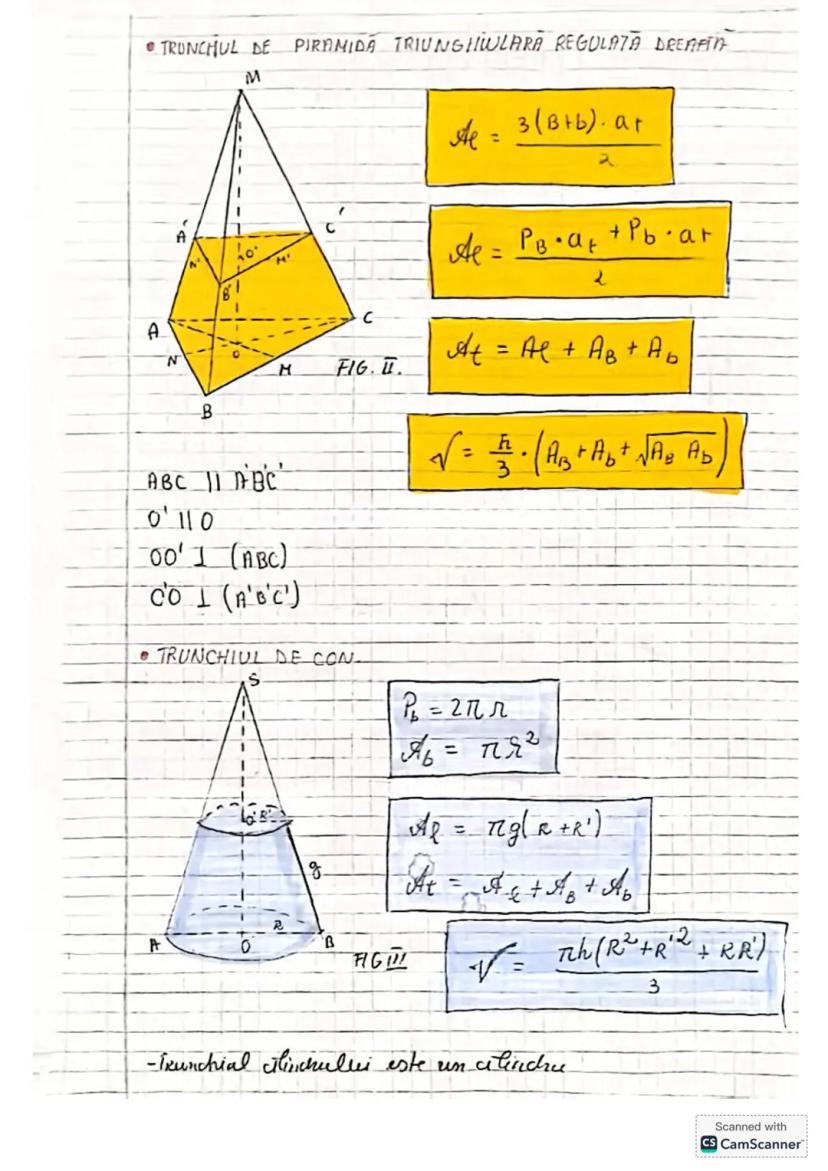
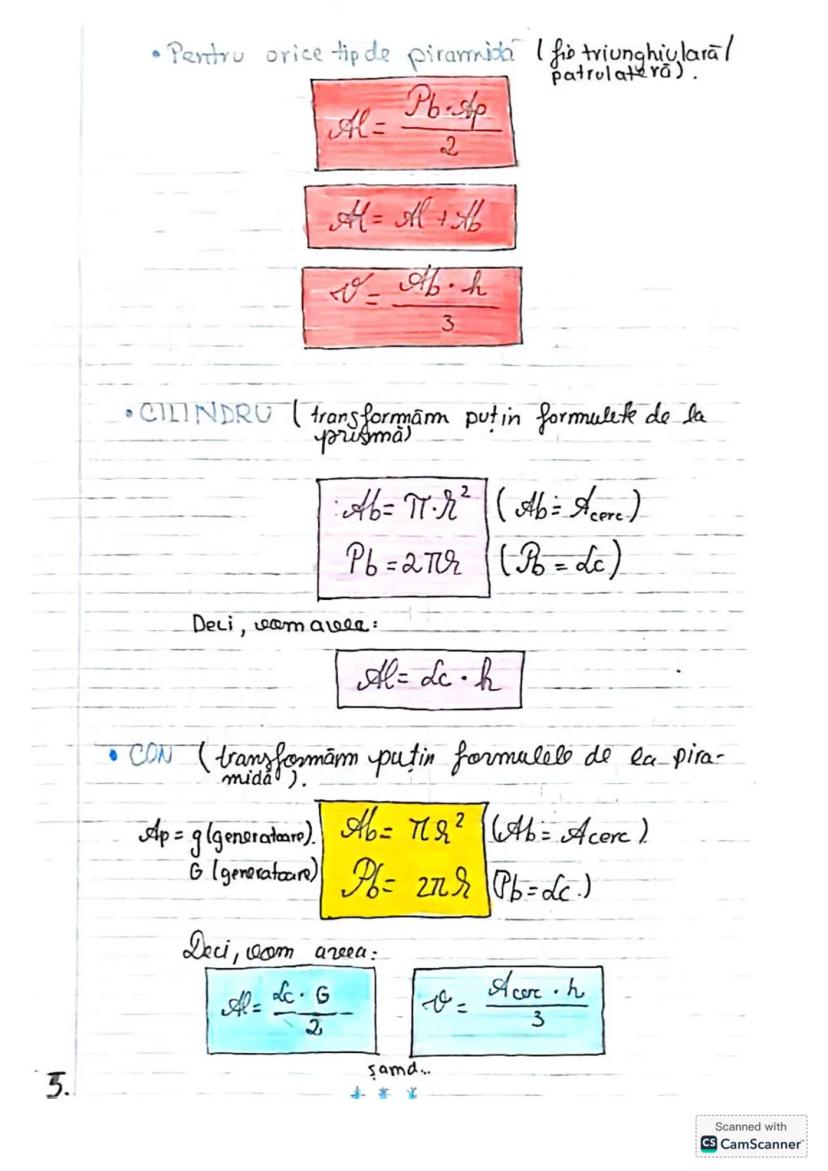
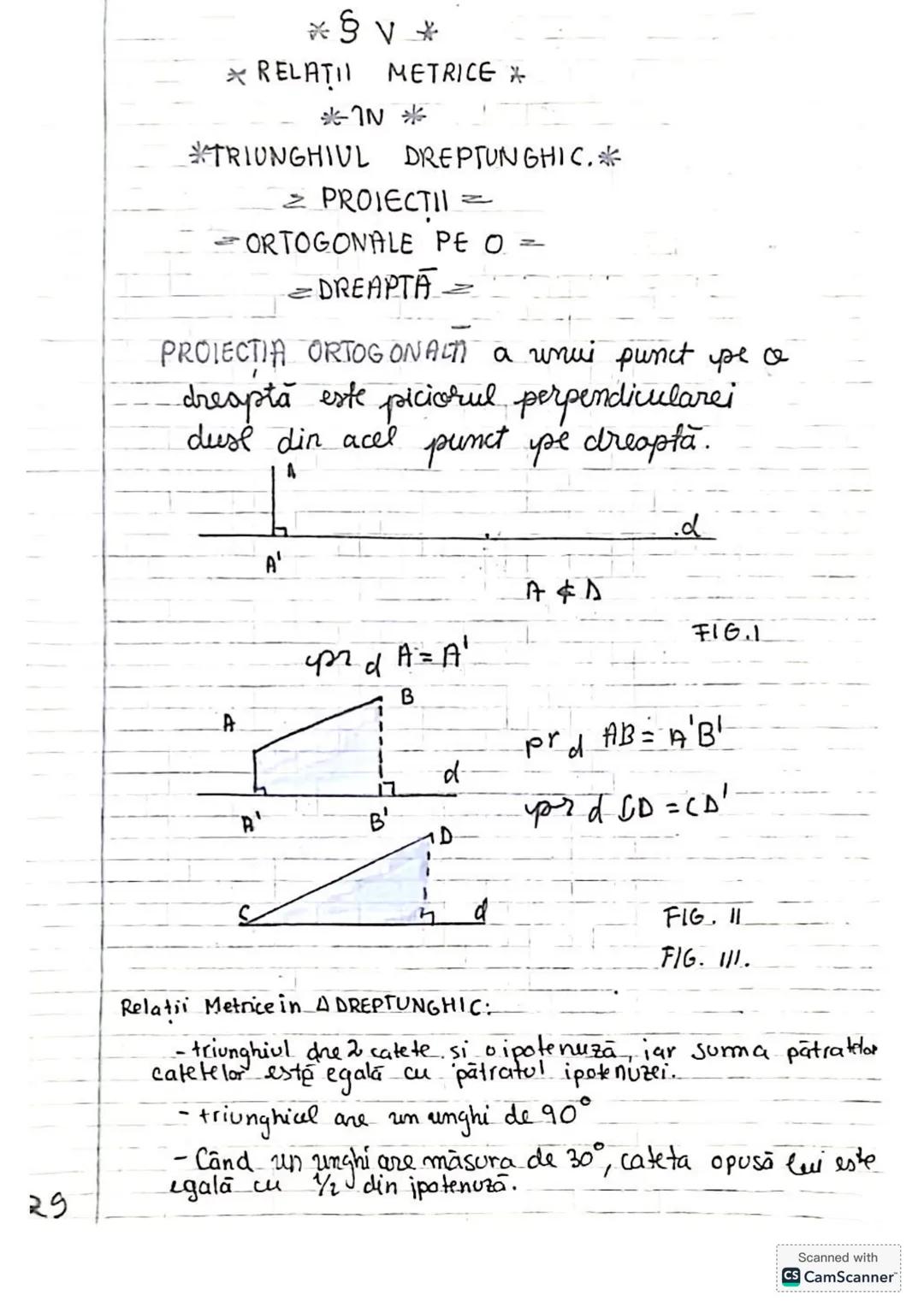
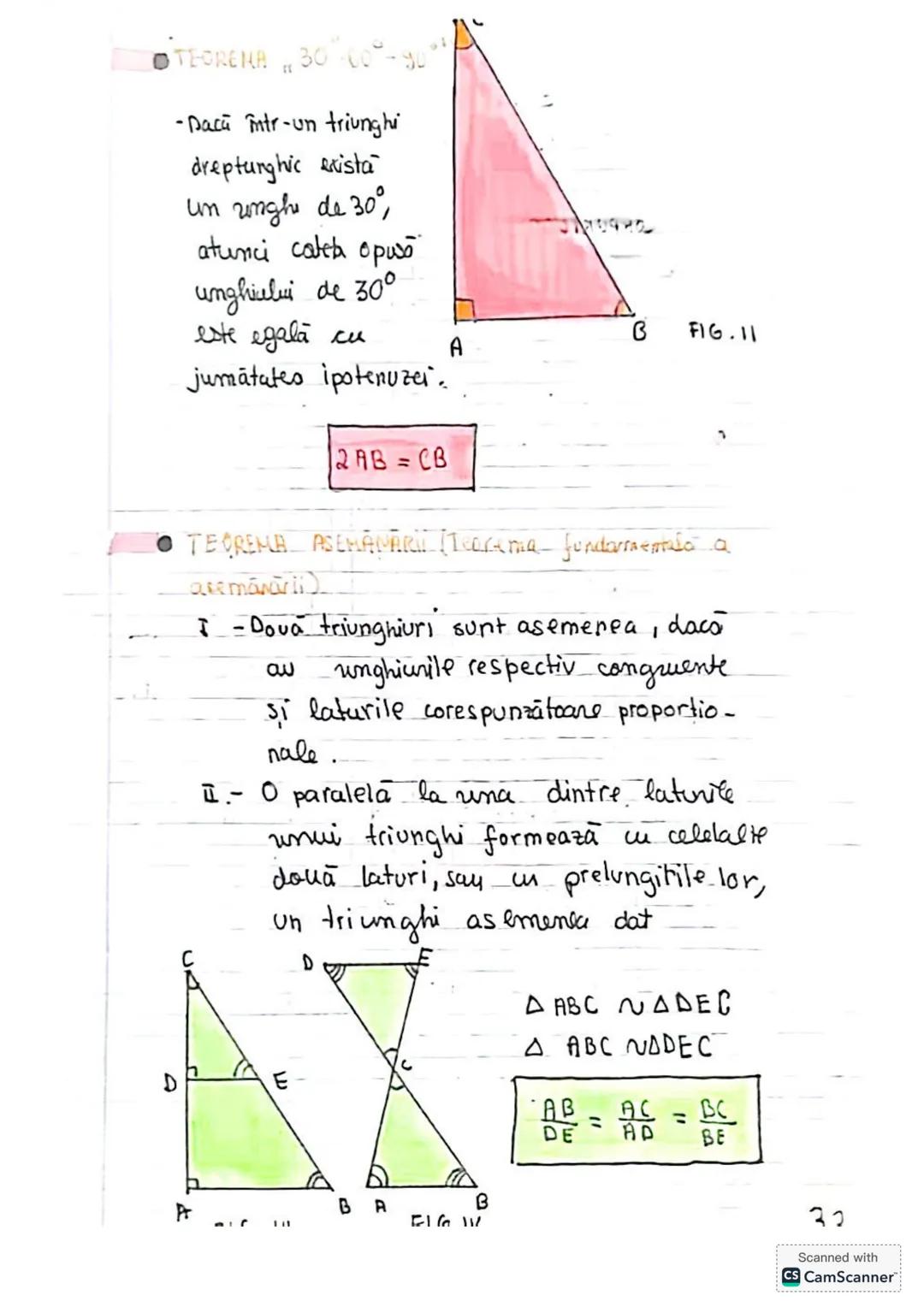
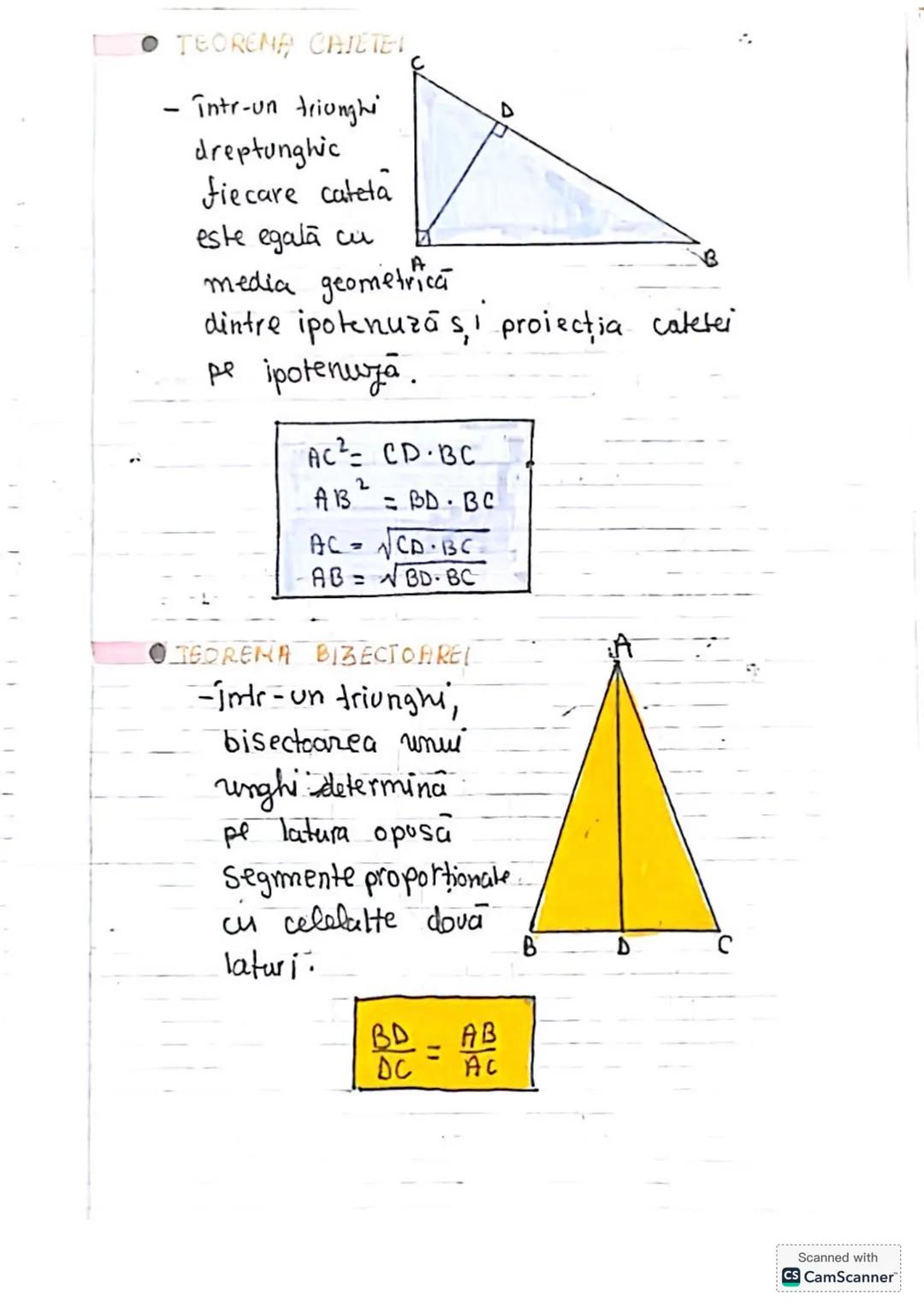
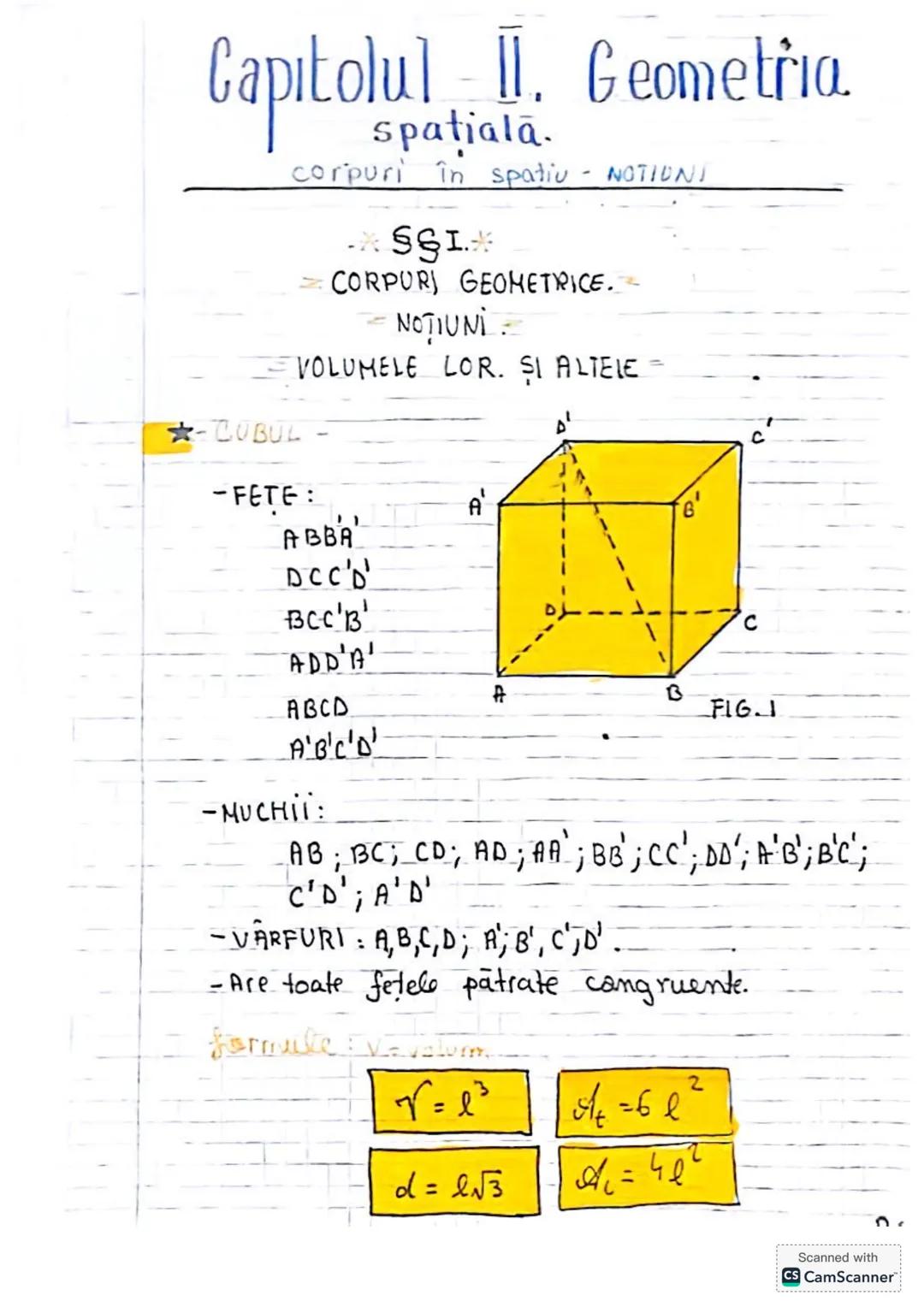
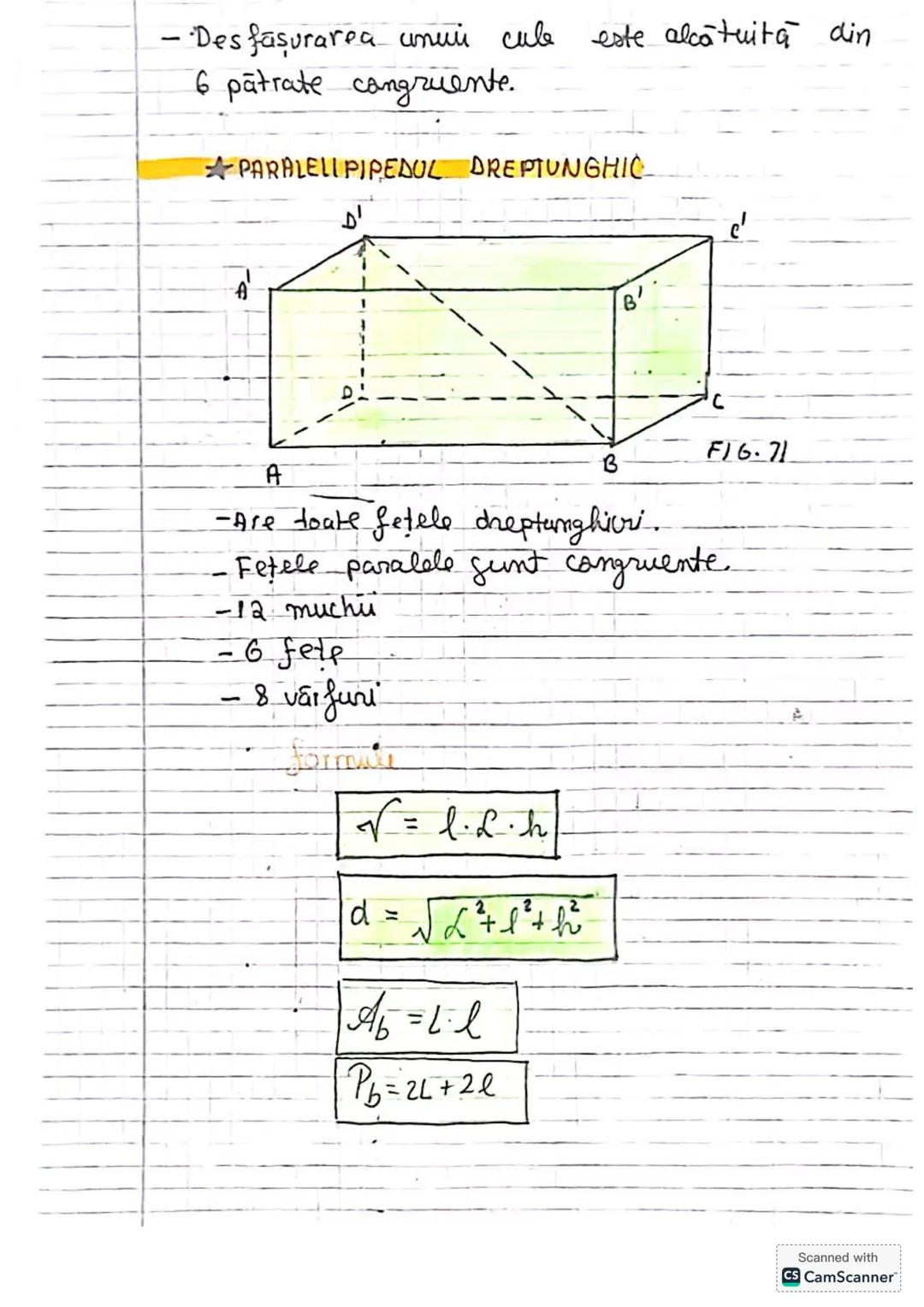
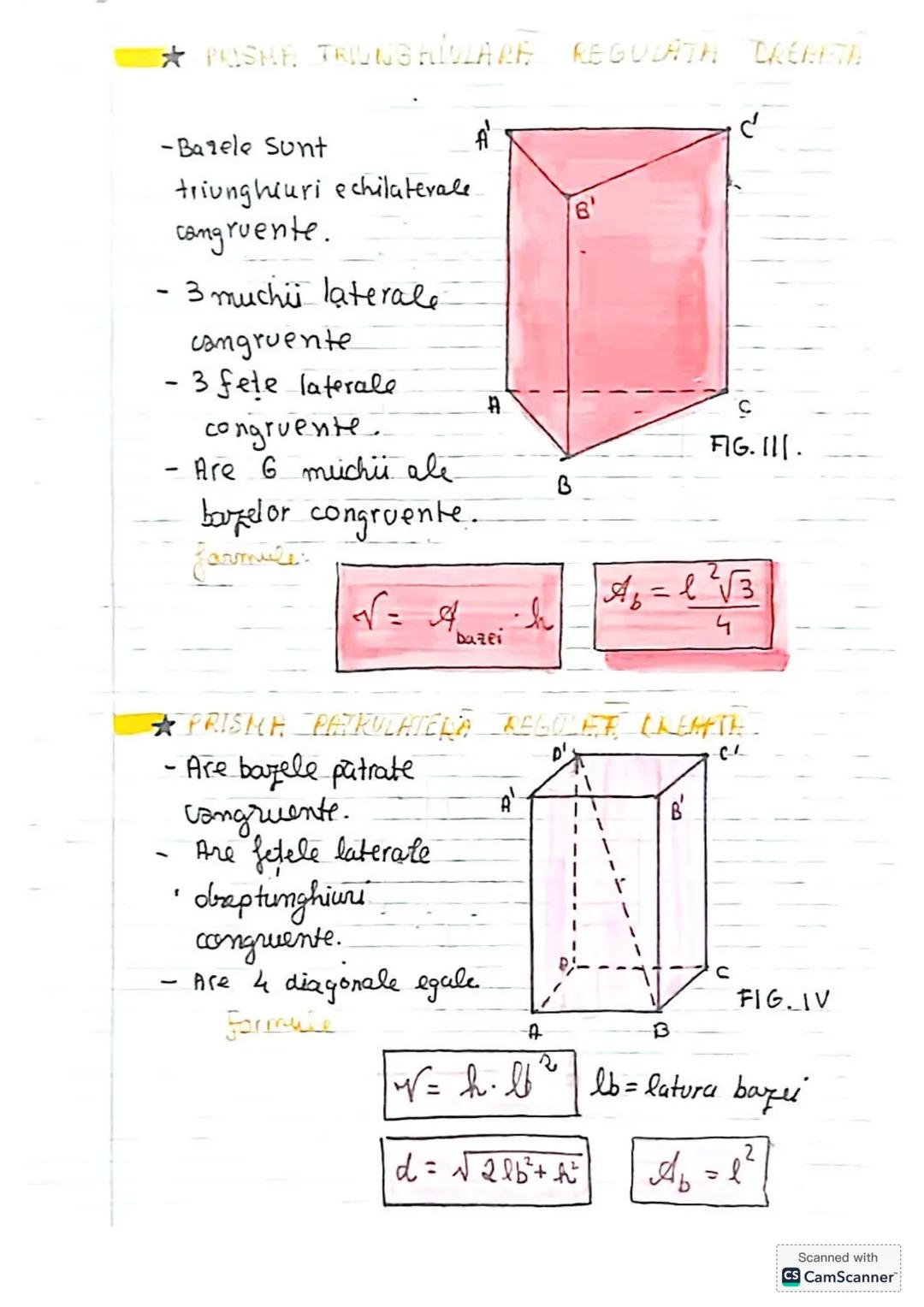
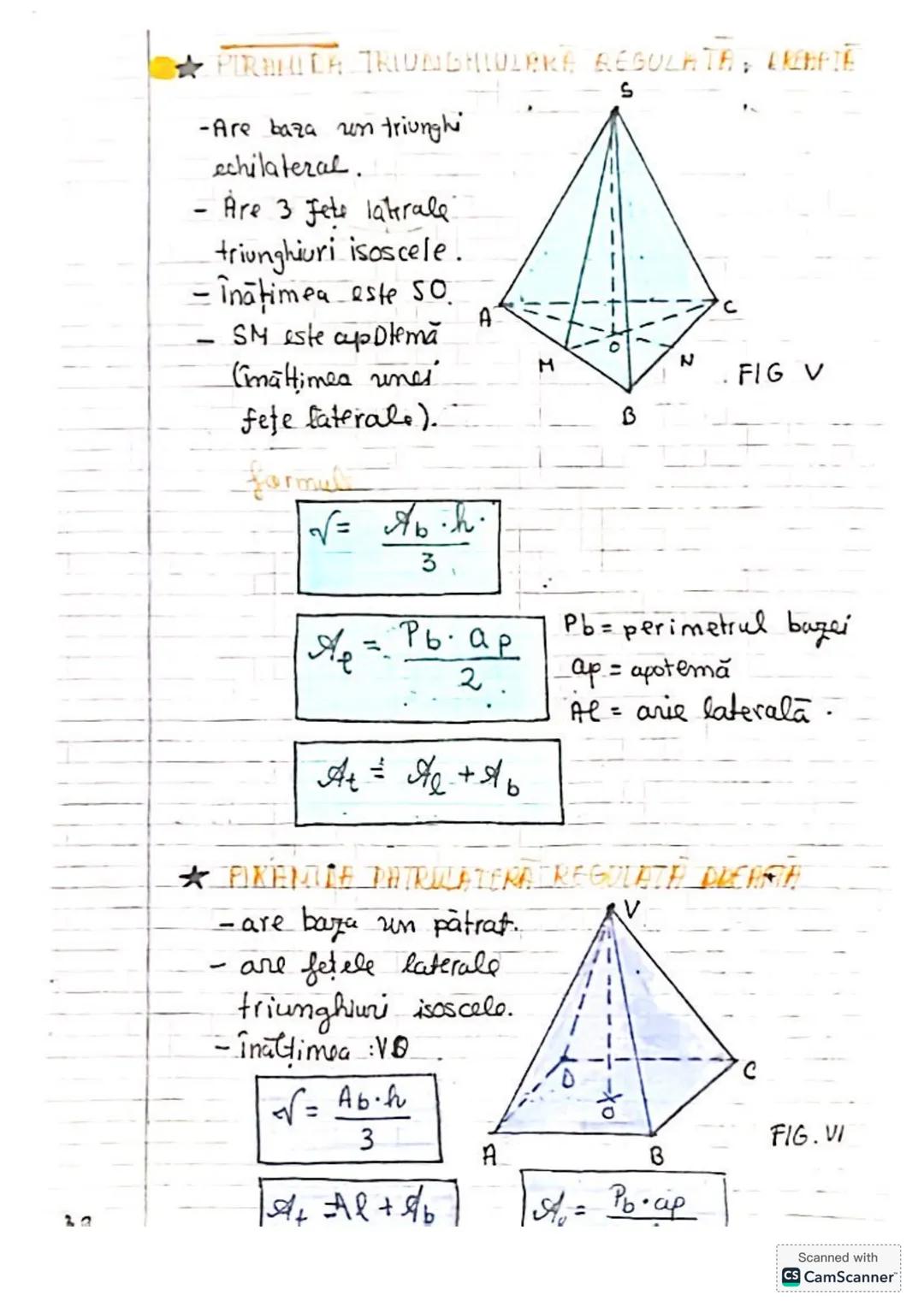
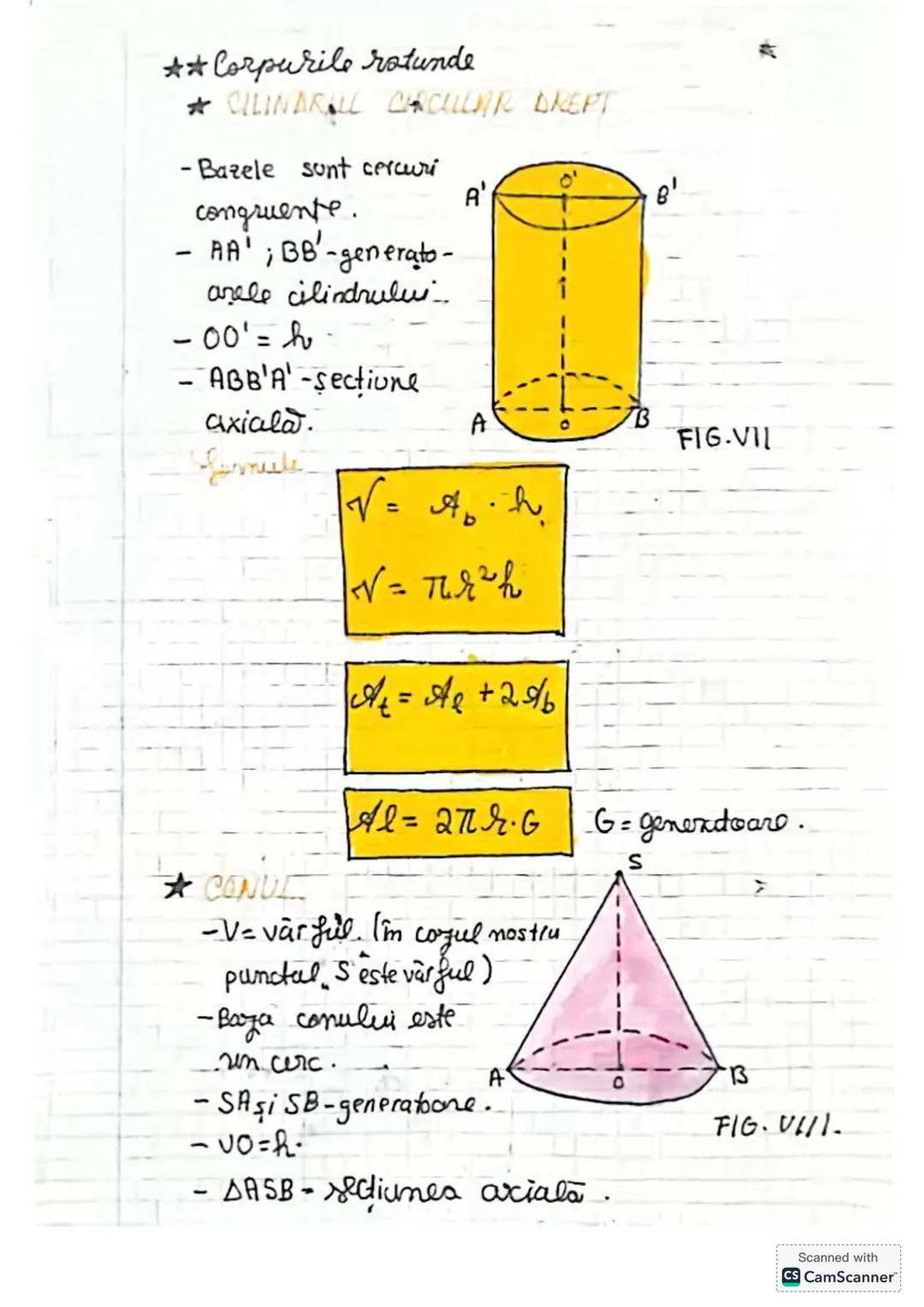
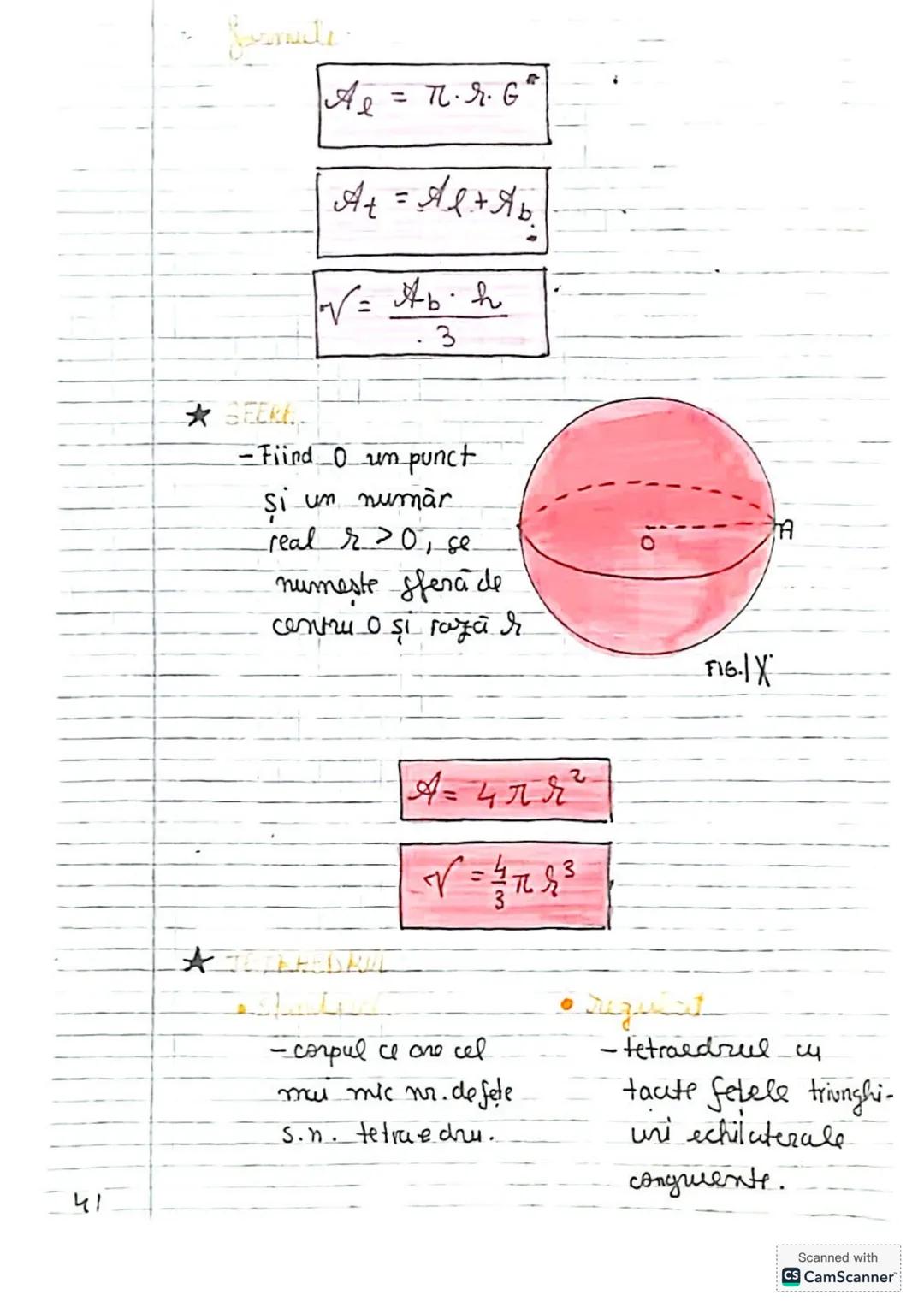
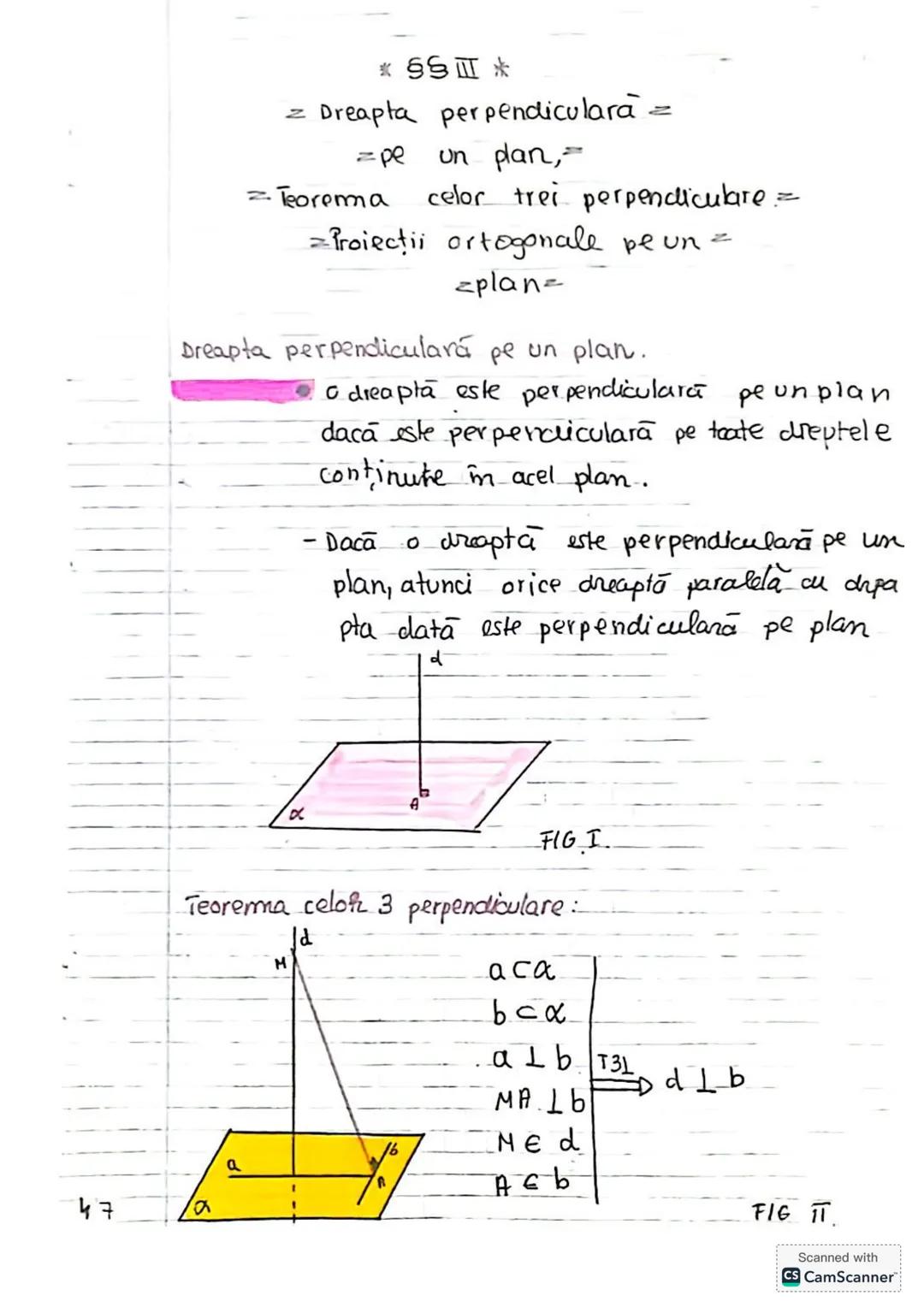
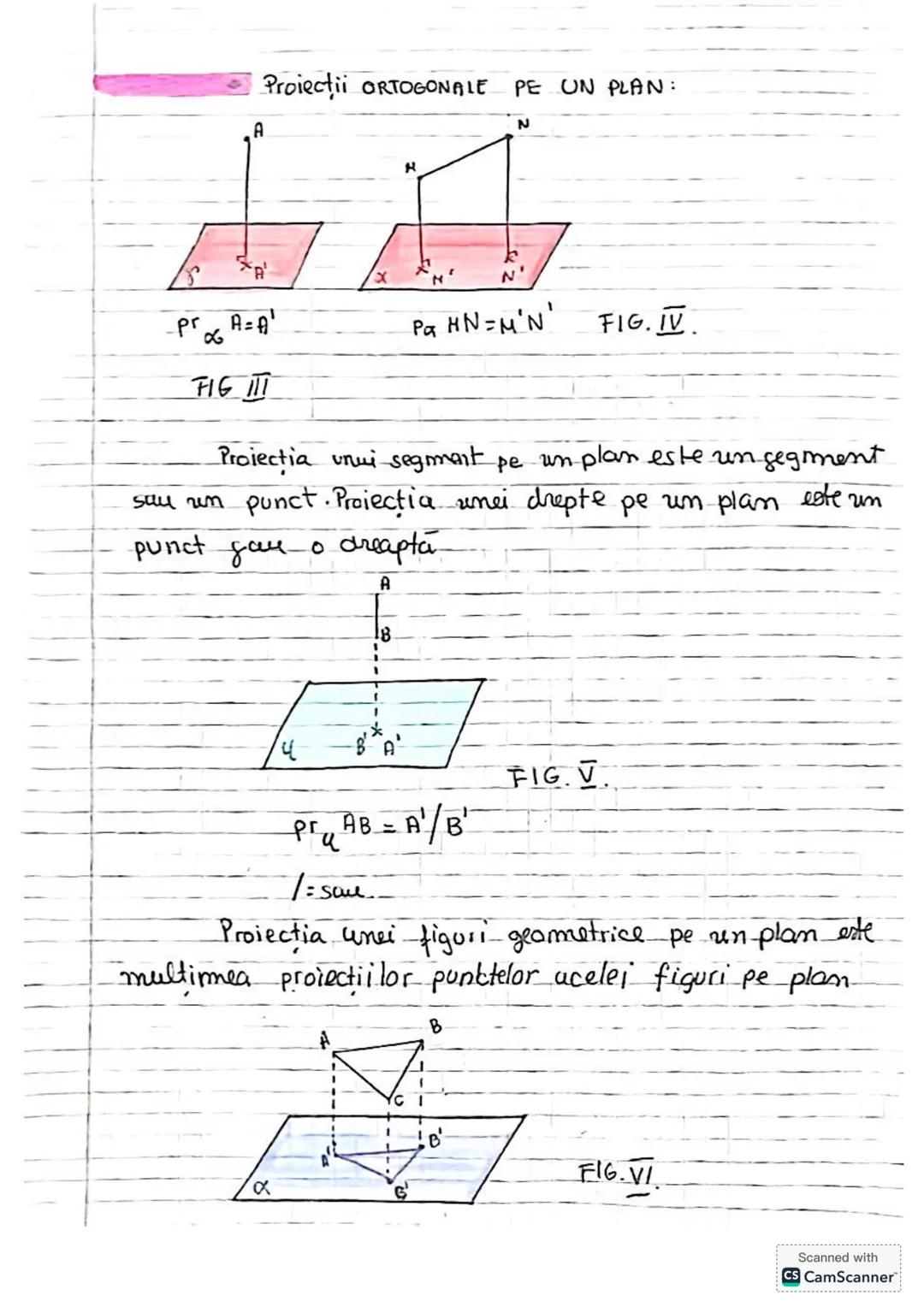
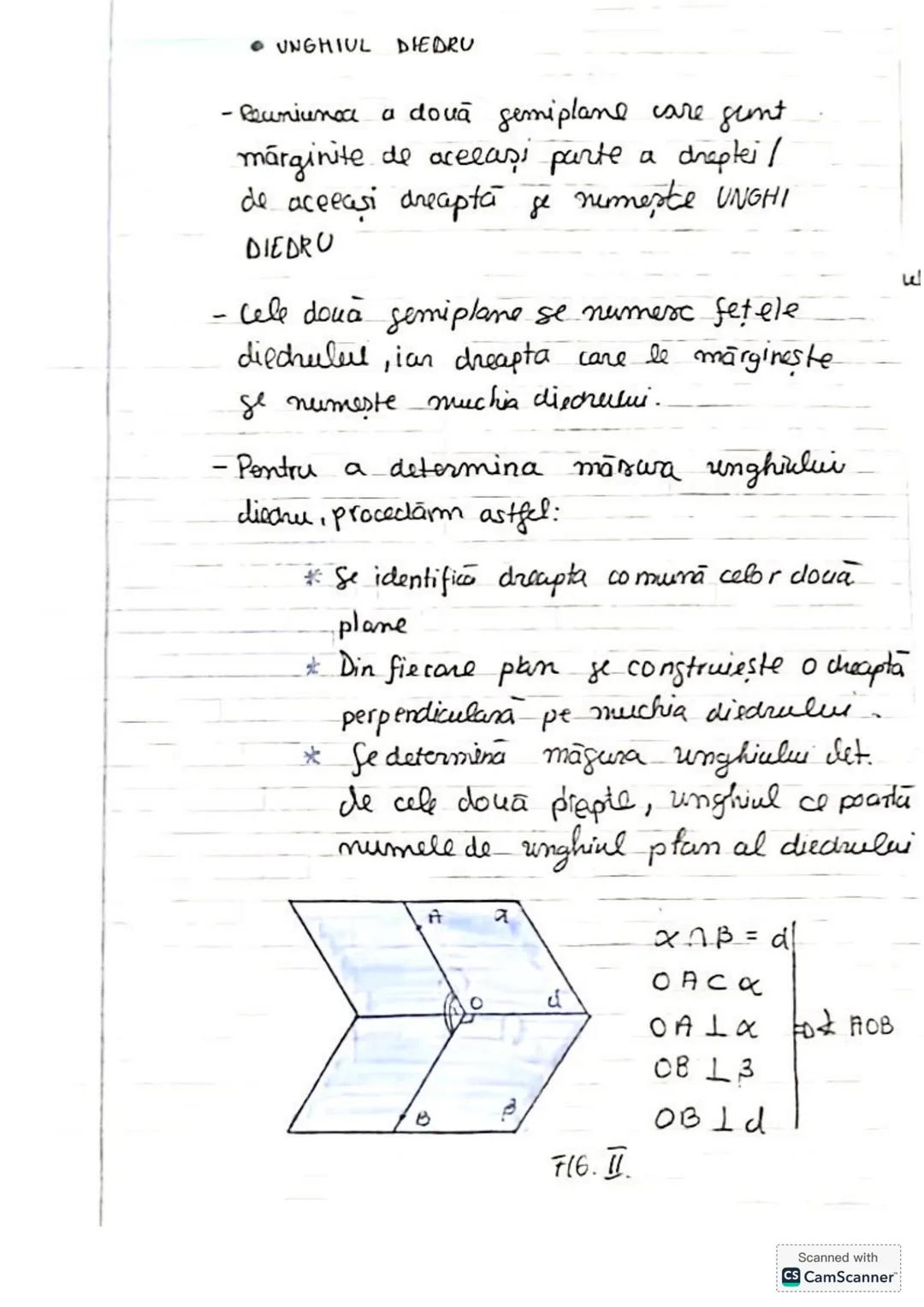
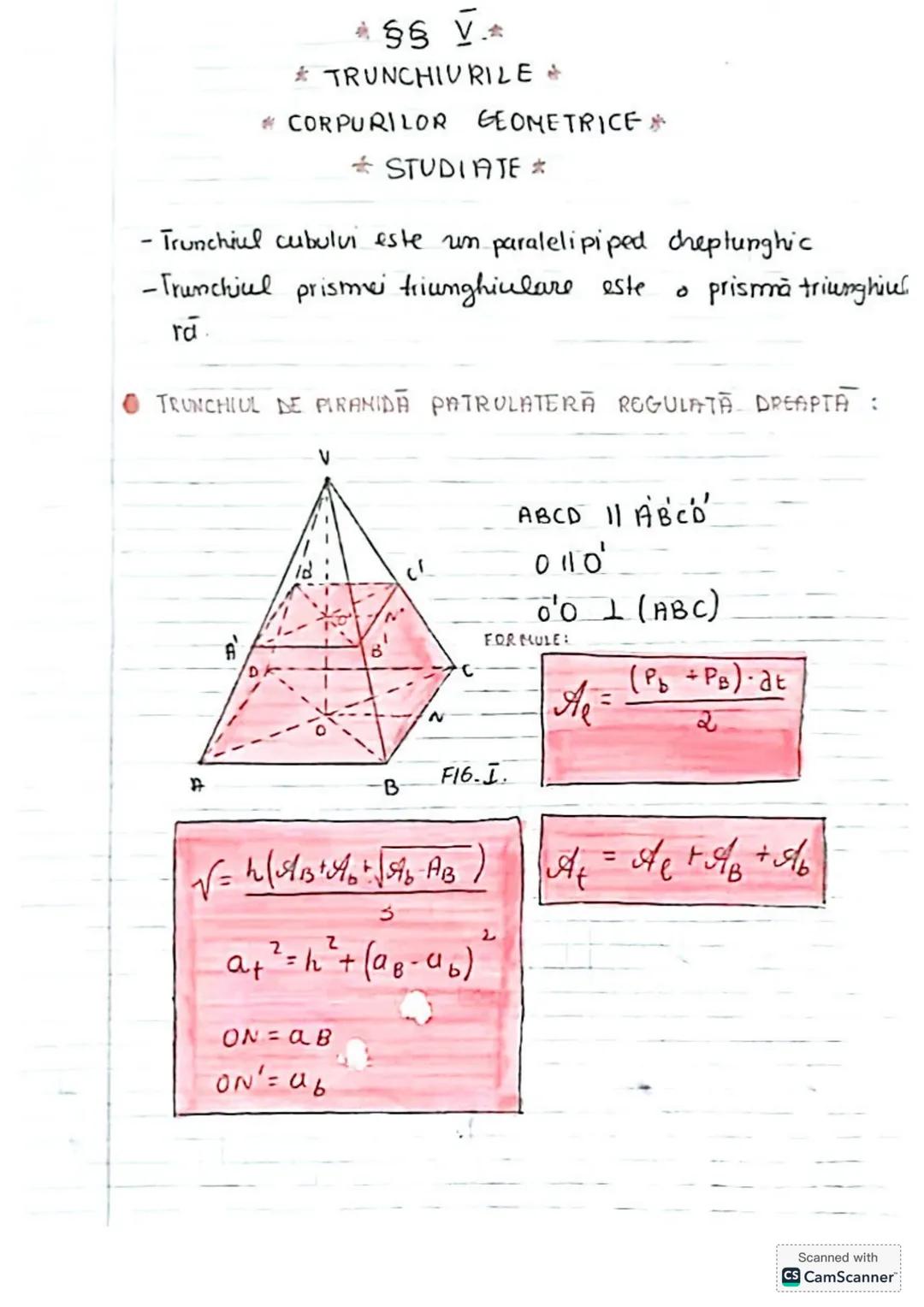
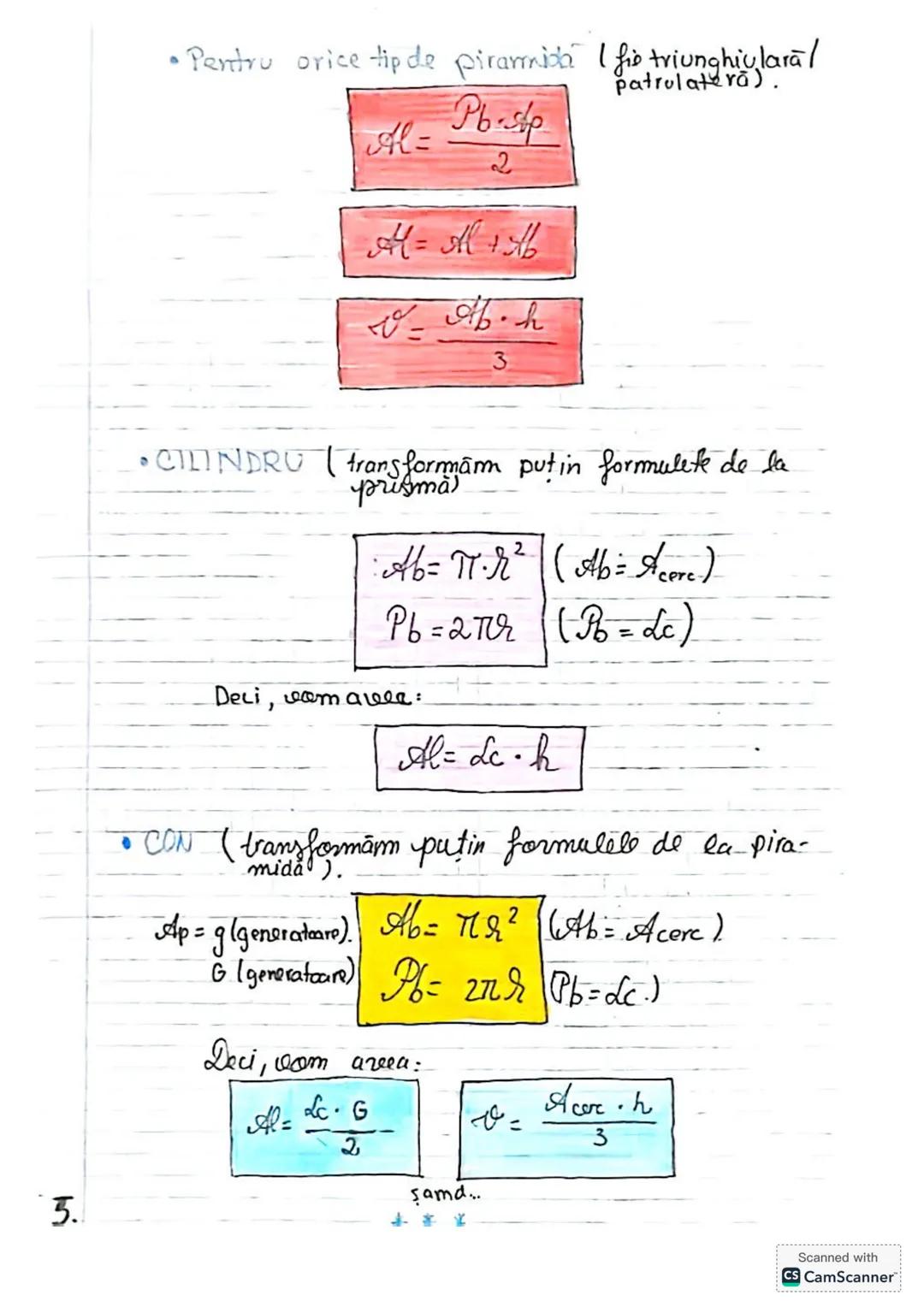
Să descoperim concepte esențiale de trigonometrie și geometrie! Vom învăța... Afișează mai mult
Înscrie-te pentru a vedea CONȚINUTULE gratuit!
Acces la toate documentele
Îmbunătățește notele tale!
Alătură-te milioanelor de elevi
Prin înregistrare, accepți Termenii de serviciu și Politica de confidențialitate