Formule Matematice - Introducere

Acest material conține formule matematice esențiale organizate pe domenii, pentru a te ajuta să rezolvi eficient probleme și exerciții. Cuprinsul include secțiuni dedicate calculului prescurtat, progresiilor, funcțiilor, trigonometriei, sistemelor de ecuații și multor alte concepte matematice importante pentru clasa a XII-a.

Indiferent dacă te pregătești pentru teste, teze sau bacalaureat, aceste formule îți vor servi ca instrument de referință rapid. Reține că înțelegerea conceptelor din spatele formulelor este la fel de importantă ca memorarea lor.

Cuprins

Materialul este structurat pe următoarele secțiuni principale:

• Formule de calcul prescurtat, inegalități, modul
• Progresii
• Funcții și ecuații de gradul I și II
• Vectori
• Trigonometrie
• Puteri, radicali și logaritmi
• Numere complexe
• Funcții și combinatorică
• Geometrie analitică
• Permutări și matrice
• Determinanți
• Sisteme de ecuații liniare
• Șiruri și asimptote
• Limite și continuitate
• Derivate și primitive
• Integrale și proprietăți

Pro-tip: Când te pregătești pentru examen, concentrează-te mai întâi pe formulele care apar frecvent în subiectele de bacalaureat, precum cele din trigonometrie, analiză matematică și algebră.

Trigonometrie

Funcțiile trigonometrice sunt definite pe domenii specifice:

• sin: ℝ → [-1, 1]
• cos: ℝ → [-1, 1]
• tg: ℝ \ {π/2 + 2kπ | k ∈ ℤ} → ℝ
• ctg: ℝ \ {kπ | k ∈ ℤ} → ℝ

Relații fundamentale:

• tg t = sin t / cos t
• ctg t = cos t / sin t
• sin²t + cos²t = 1 (identitatea fundamentală)

Proprietăți pentru argumente negative:

• cos$-t$ = cos t
• sin$-t$ = -sin t
• tg$-t$ = -tg t
• ctg$-t$ = -ctg t

Pentru funcțiile inverse:

• arcsin$-x$ = -arcsin x
• arccos$-x$ = π - arccos x
• arctg$-x$ = -arctg x
• arcctg$-x$ = π - arcctg x

Atenție! Memorează valorile exacte pentru unghiurile de 0°, 30°, 45°, 60° și 90°. Acestea apar frecvent în probleme și te ajută să verifici rapid rezultatele.

Formule de reducere la primul cadran:

• cos$90° - t$ = sin t
• sin$90° - t$ = cos t
• cos$180° - t$ = -cos t
• sin$180° - t$ = sin t

Domeniile funcțiilor inverse:

• arcsin: [-1, 1] → [-π/2, π/2]
• arccos: [-1, 1] → [0, π]
• arctg: ℝ → (-π/2, π/2)
• arcctg: ℝ → (0, π)

Formulele pentru sumă, diferență și dublarea unghiurilor sunt esențiale pentru simplificarea expresiilor trigonometrice complexe!

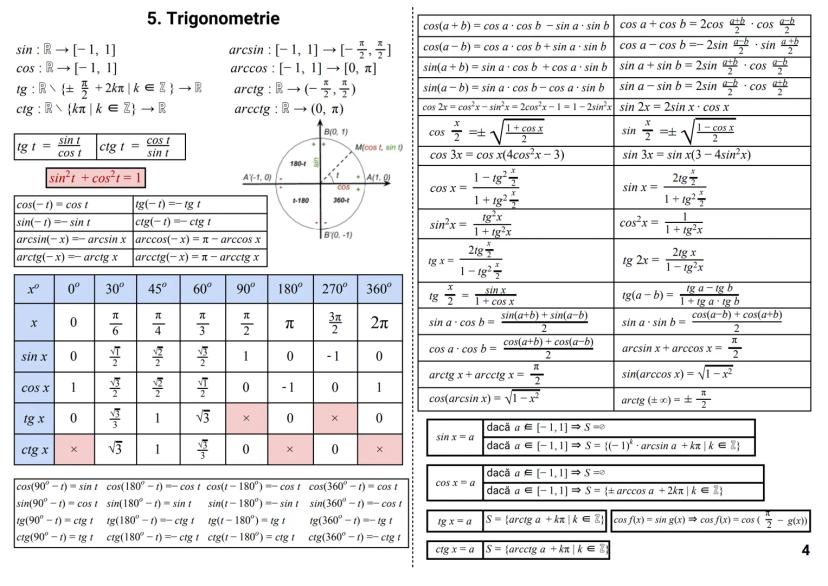
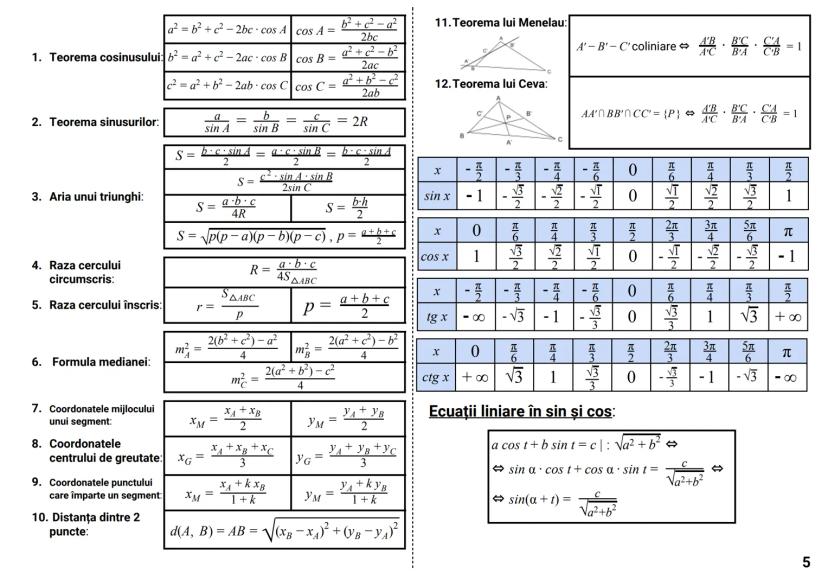
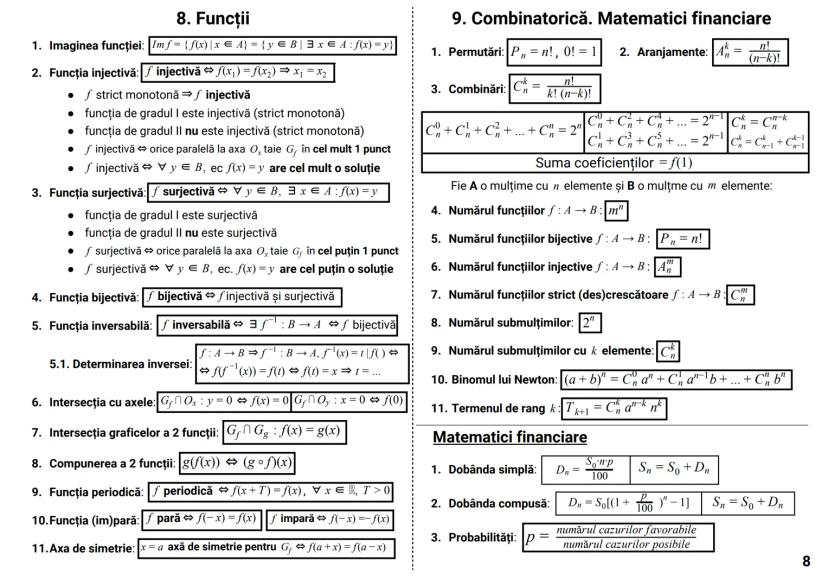
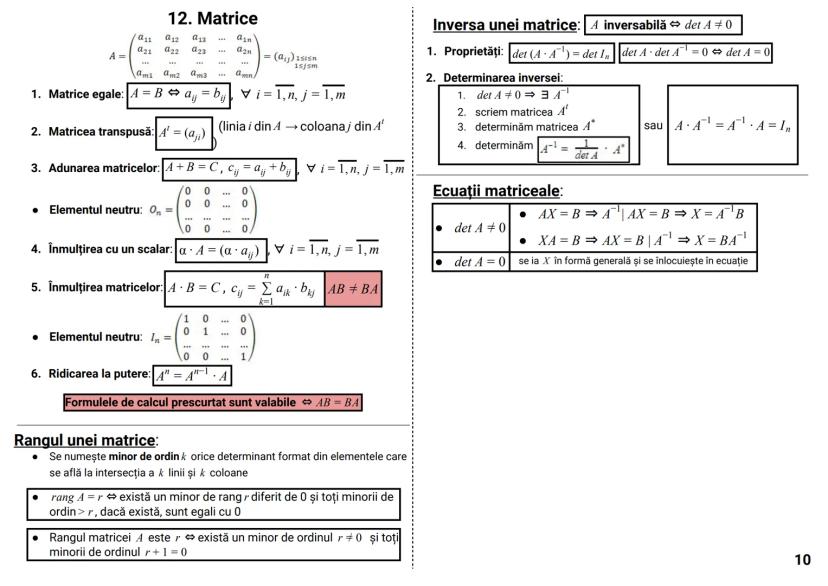
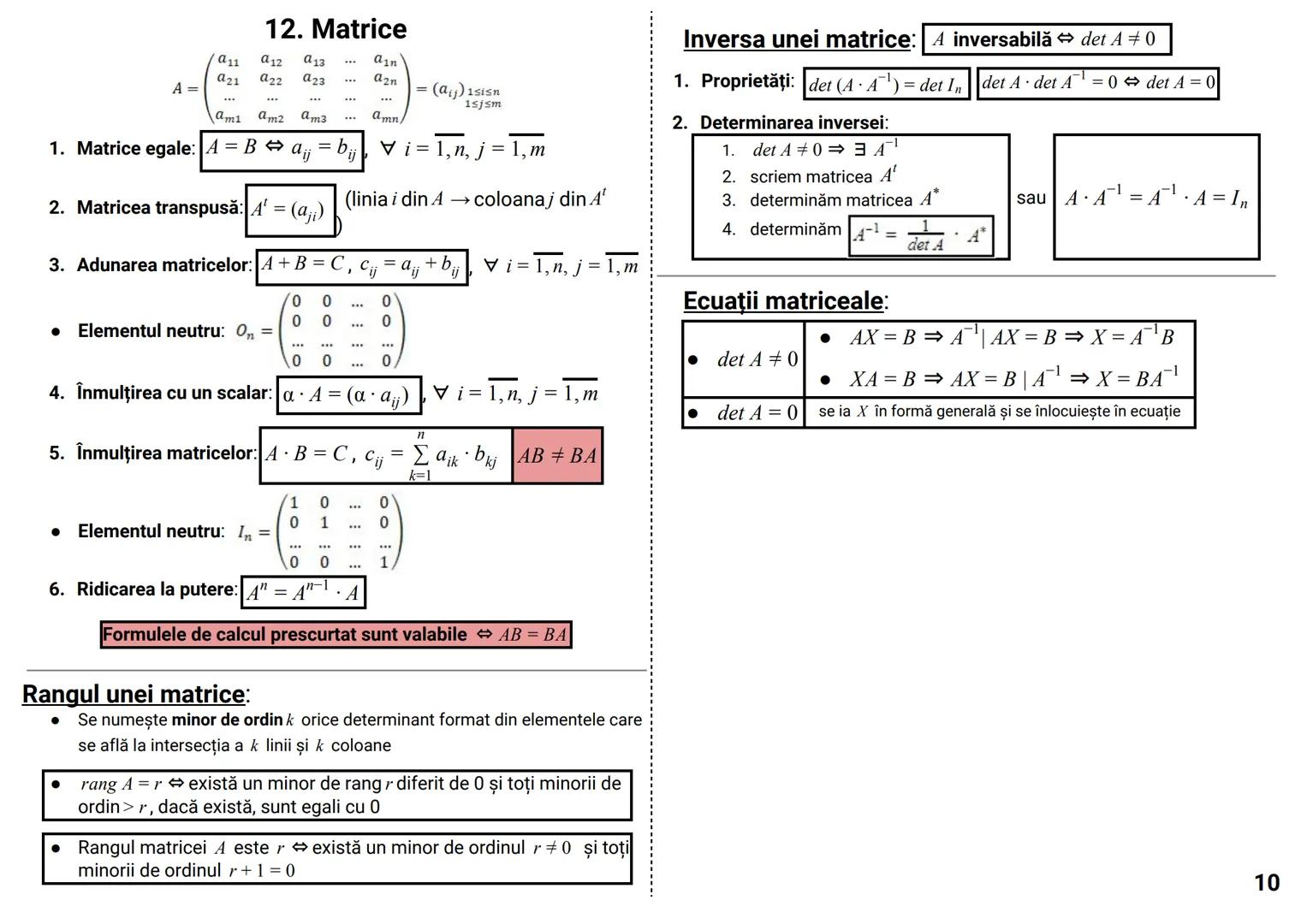
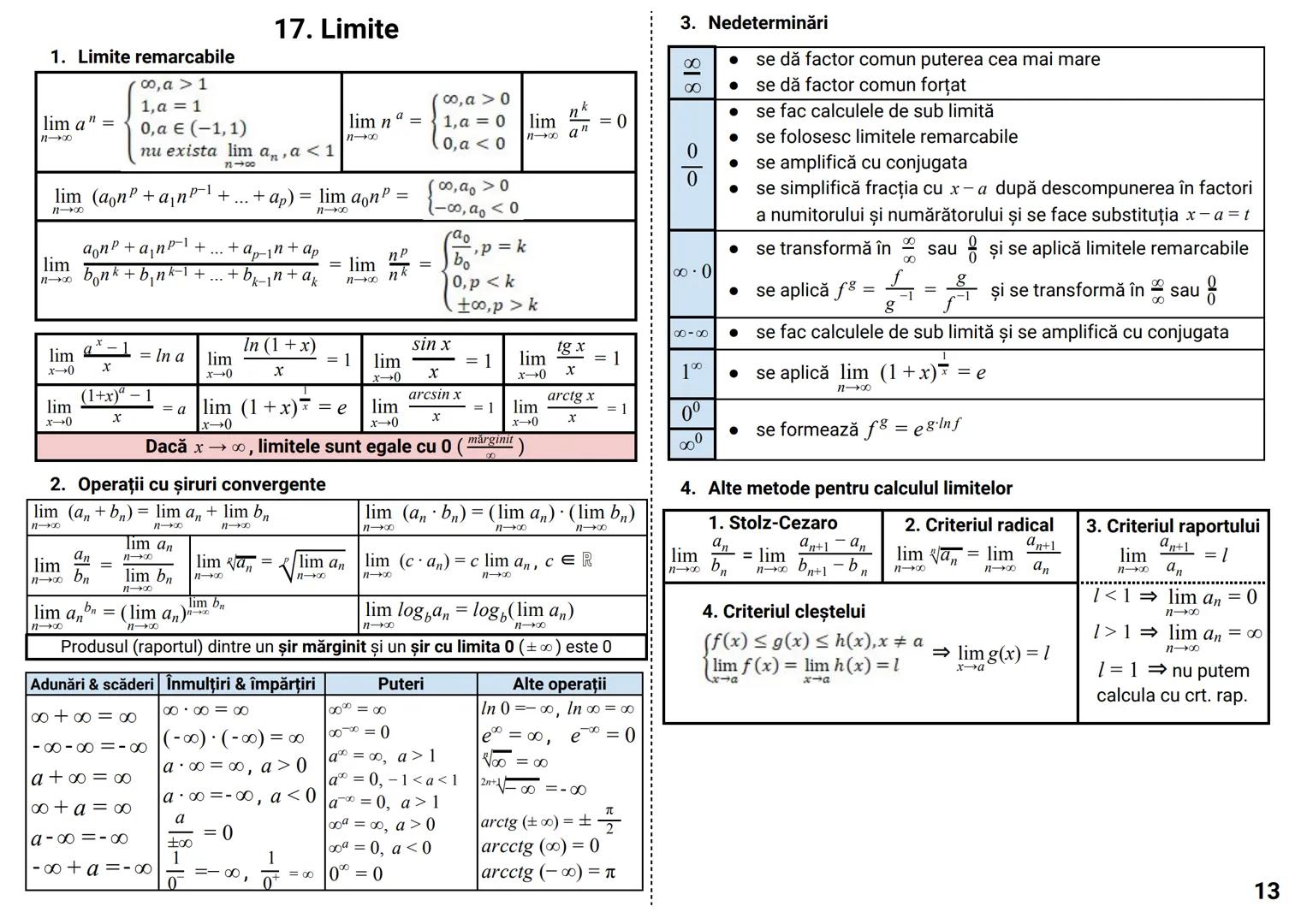
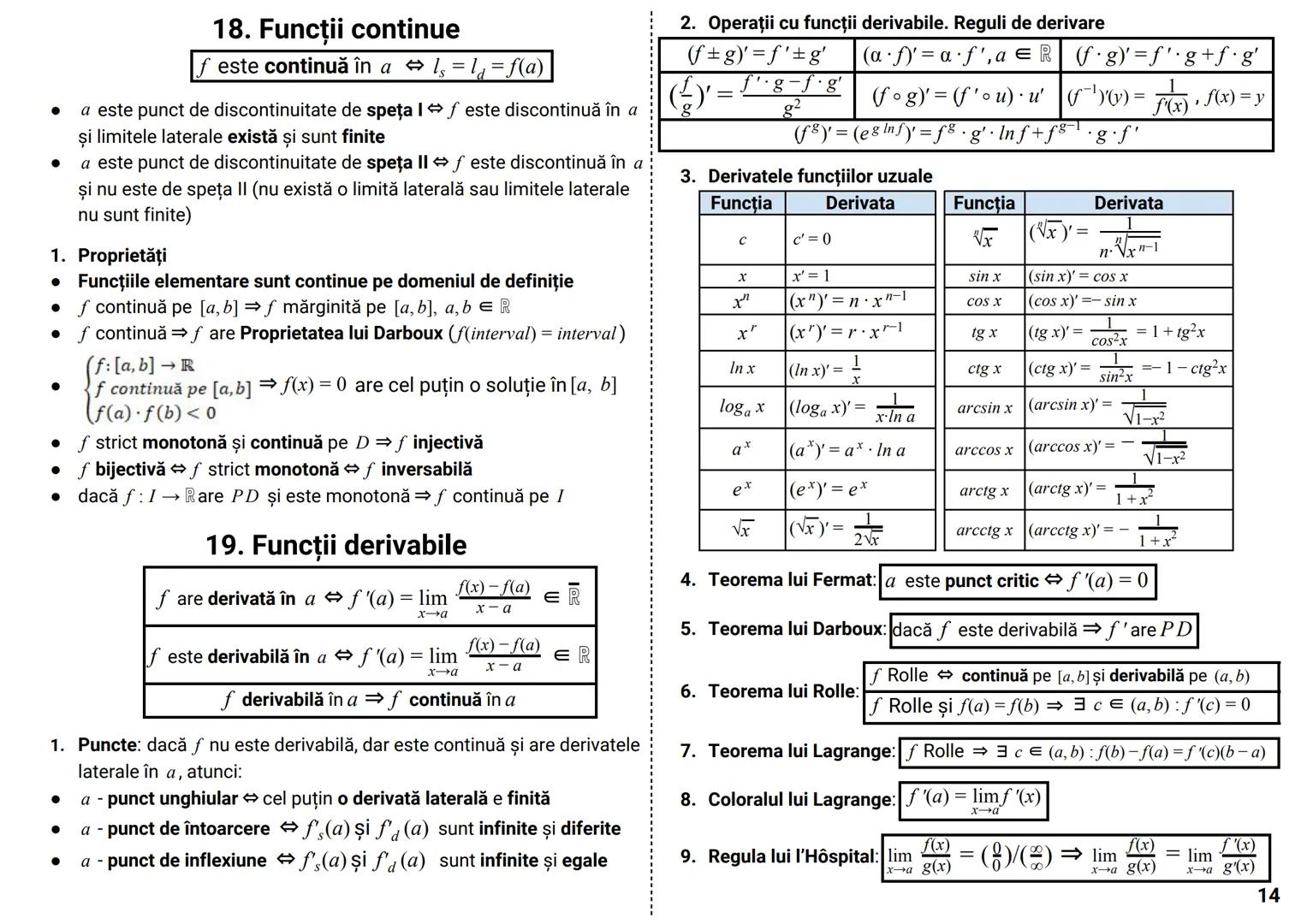
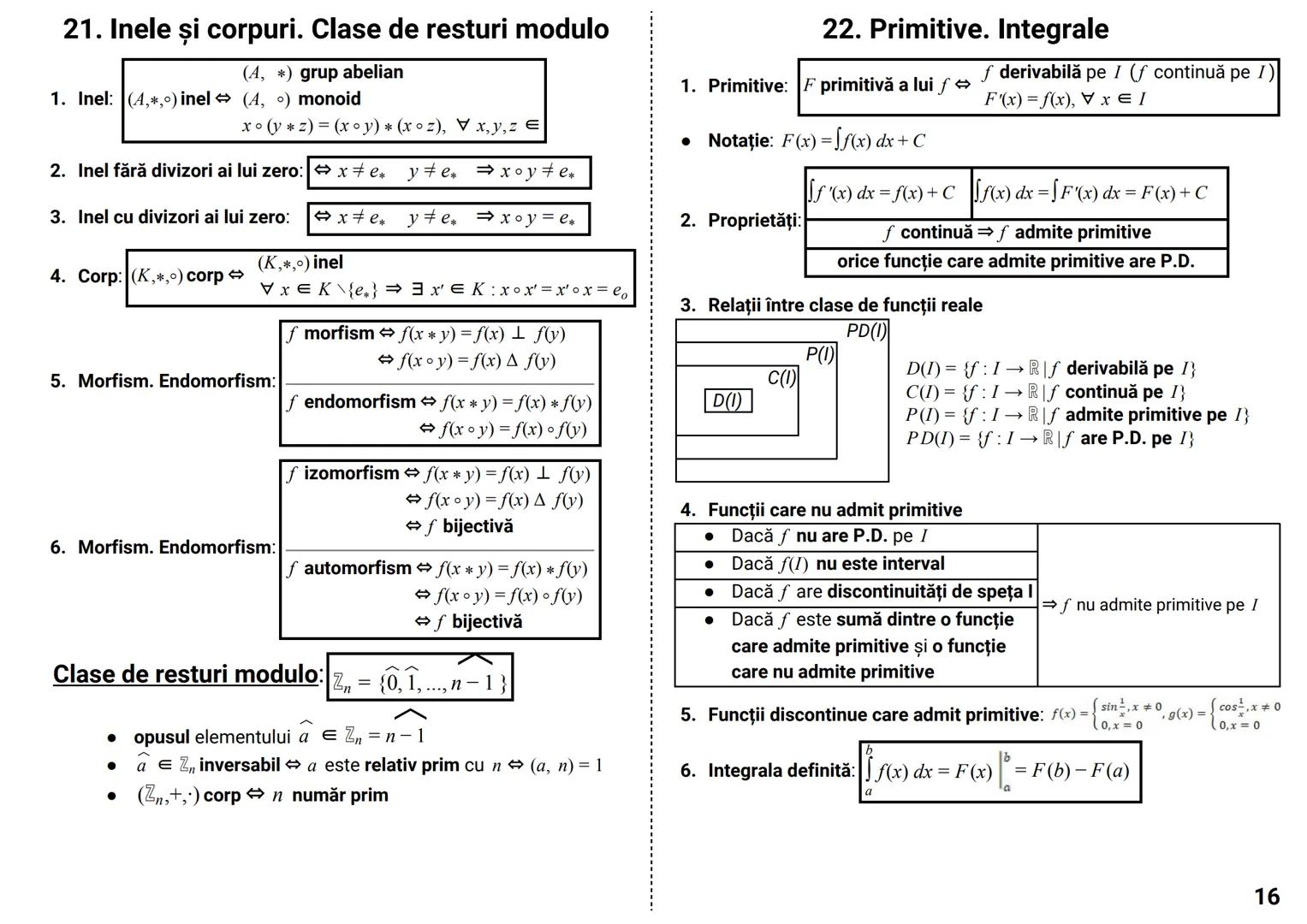
Determinanți

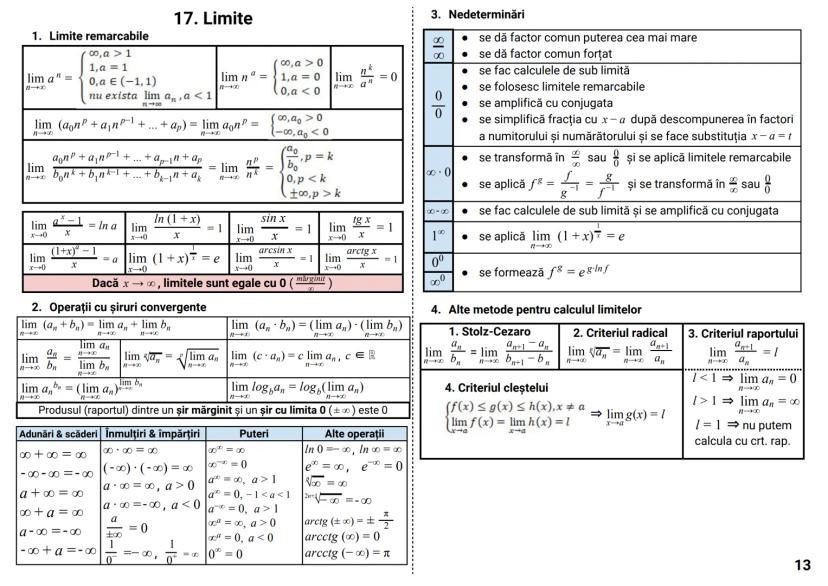
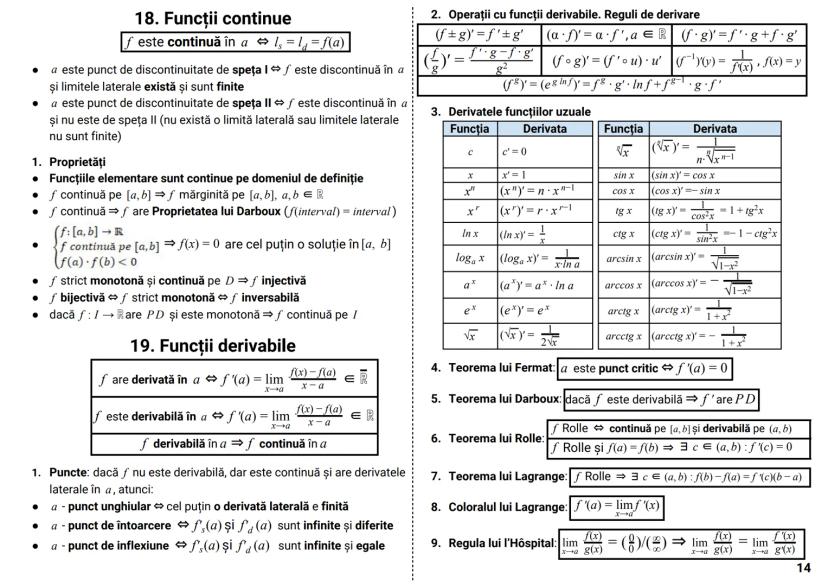
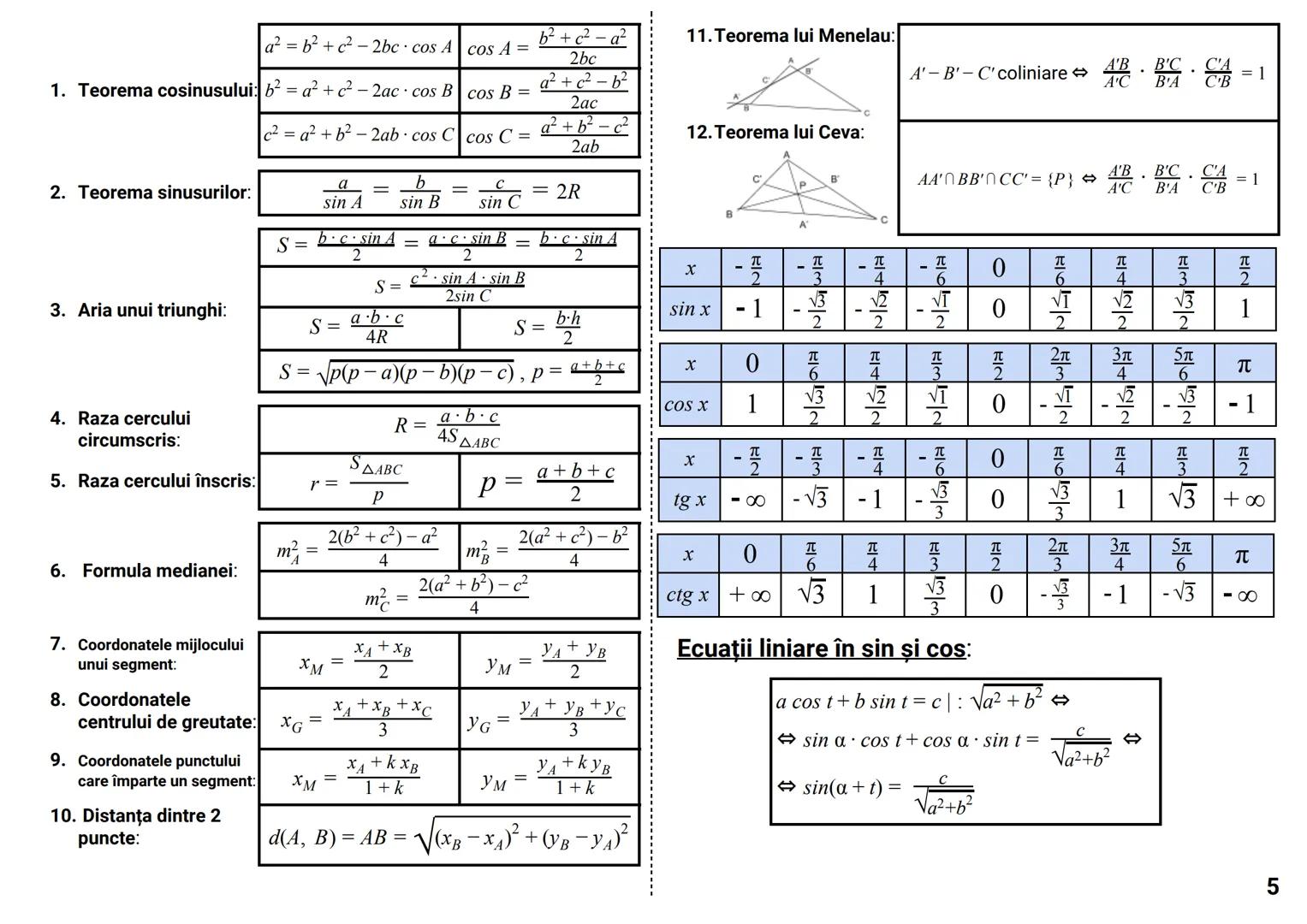
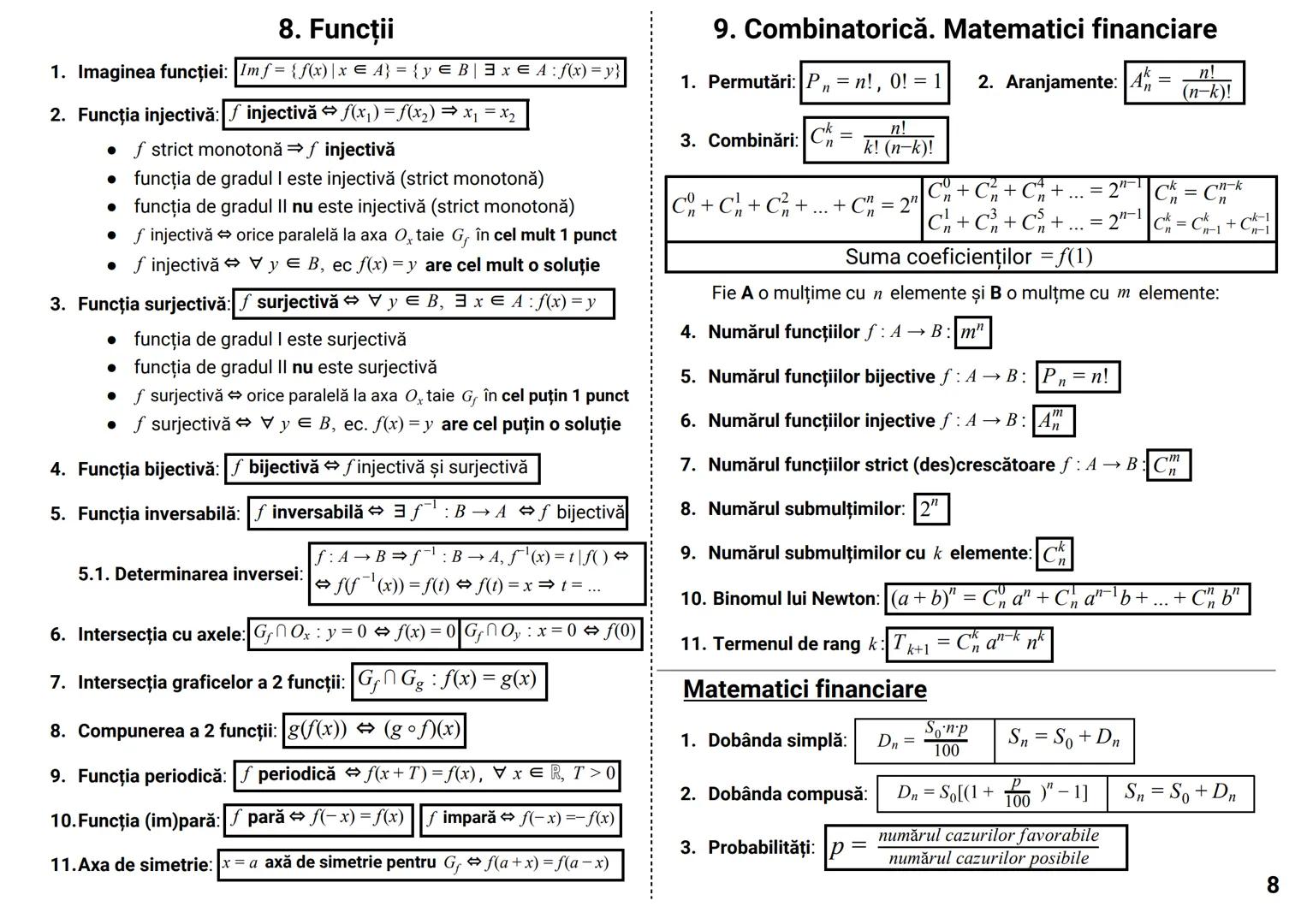
Determinantul unei matrice este un număr asociat unei matrice pătratice, care oferă informații importante despre aceasta.

Pentru o matrice de ordinul 2:

|a b|
|c d| = ad - bc

Pentru o matrice de ordinul 3:

|a b c|
|d e f| = aei + dhc + gbf - ceg - fha - idb

Dezvoltarea unui determinant se poate face după orice linie sau coloană:

|a b c|
|d e f| = a·|e f| - b·|d f| + c·|d e|
|g h i|   |h i|   |g i|   |g h|

Proprietăți importante:

• det A^t = det A (determinantul transpusei este egal cu determinantul matricei)
• det(AB) = det A · det B (determinantul produsului este produsul determinanților)
• det(αA) = α^n · det A (pentru o matrice de ordin n)

Cazuri speciale când determinantul este zero:

1. O linie/coloană are toate elementele zero
2. Două linii/coloane identice
3. O linie/coloană este combinație liniară a altora

Sfat util: Folosește proprietatea că poți adăuga multipli ai unei linii/coloane la altă linie/coloană fără a schimba valoarea determinantului. Acest lucru poate simplifica mult calculele!

Determinantul circular:

|a b c|
|c a b| = a³ + b³ + c³ - 3abc
|b c a|

Determinantul Vandermonde:

|1 1 1  |
|a b c  | = (b-a)(c-a)(c-b)
|a² b² c²|

Teorema Cayley-Hamilton: A² - tr(A)·A + det A·I₂ = O₂, unde tr(A) = a + d

Sisteme de ecuații liniare

Un sistem de ecuații liniare poate fi scris matricial ca: AX = B

Compatibilitatea unui sistem:

• Incompatibil: nu are soluții ⟺ rang Ā ≠ rang A
• Compatibil: are cel puțin o soluție ⟺ rang Ā = rang A

Tipuri de sisteme compatibile:

• Determinat: are soluție unică ⟺ rang A = rang Ā = nr. necunoscute, det A ≠ 0
• Nedeterminat: are infinitate de soluții ⟺ rang A = rang Ā < nr. necunoscute

Pentru sistemele omogene $B = 0$:

• Au întotdeauna soluția trivială (0, 0, ..., 0)
• Au doar soluția trivială ⟺ rang A = nr. necunoscute, det A ≠ 0
• Au și soluții netriviale ⟺ rang A < nr. necunoscute, det A = 0

Important pentru examene: Când analizezi un sistem, verifică întâi compatibilitatea, apoi determinarea. Pentru sistemele nedeterminate, identifică parametrii și exprimă soluția generală în funcție de aceștia.

Sisteme simetrice:

1. Notăm S = x + y și P = xy
2. Formăm un sistem cu necunoscutele S și P
3. Rezolvăm sistemul obținut
4. Pentru a afla x și y, rezolvăm ecuația t² - St + P = 0

Metode de rezolvare a sistemelor și șiruri

Metode pentru sisteme liniare

Regula lui Cramer (pentru sisteme compatibil determinate):

• Calculăm det A
• Dacă det A ≠ 0, calculăm determinanții d₁, d₂, ..., d_n
• Soluția este x_k = d_k / det A

Metoda matricială:

• Pentru A ∈ M_n(R), calculăm det A
• Dacă det A ≠ 0, calculăm A⁻¹
• Soluția este X = A⁻¹·B

Teorema lui Kronecker-Capelli: Un sistem este compatibil dacă și numai dacă rang A = rang Ā

Studiul compatibilității:

• Dacă A este pătratică și det A ≠ 0: folosim regula lui Cramer
• Dacă A nu este pătratică sau det A = 0: determinăm rangul și minorul principal

Sfat practic: Pentru sistemele mici (2×2 sau 3×3), regula lui Cramer este adesea cea mai rapidă metodă. Pentru sisteme mai mari, metoda Gauss este preferabilă.

Șiruri și asimptote

Monotonie:

• Șir crescător: a_n+1 - a_n ≥ 0 sau a_n+1/a_n ≥ 1
• Șir descrescător: a_n+1 - a_n ≤ 0 sau a_n+1/a_n ≤ 1

Convergență:

• Șir mărginit: există a, b ∈ ℝ astfel încât a ≤ a_n ≤ b
• Șir convergent: are limită finită (un șir monoton și mărginit este convergent)

Asimptote:

1. Orizontale: y = l, unde l = lim f(x) când x → ±∞
2. Oblice: y = mx + n, unde m = lim f(x)/x și n = lim $f(x) - mx$ când x → ±∞
3. Verticale: x = a, dacă lim f(x) = ±∞ când x → a (a este punct de acumulare pentru domeniu)

Limite și tehnici de calcul

Limite remarcabile

Pentru șiruri:

• lim a^n (n→∞) = 0 dacă |a| < 1, 1 dacă a = 1, nu există dacă |a| > 1
• lim n^a (n→∞) = ∞ dacă a > 0, 1 dacă a = 0, 0 dacă a < 0
• lim n^k/a^n (n→∞) = 0 pentru orice k și a > 1

Pentru funcții când x → 0:

• lim $e^x - 1$/x = 1
• lim ln$1 + x$/x = 1
• lim sin x/x = 1
• lim tg x/x = 1
• lim $1 + x$^α - 1)/x = α

Trucul matematic: Pentru multe nedeterminări de forma 0/0 sau ∞/∞, poți folosi regula lui L'Hospital: lim f(x)/g(x) = lim f'(x)/g'(x) dacă ambele limite conduc la nedeterminări.

Operații cu șiruri convergente

• lim $a_n + b_n$ = lim a_n + lim b_n
• lim $a_n · b_n$ = lim a_n · lim b_n
• lim $a_n / b_n$ = lim a_n / lim b_n $dacă lim b_n ≠ 0$

Nedeterminări și tehnici de rezolvare

• ∞/∞: factorizăm cu cea mai mare putere
• 0/0: factorizare, limite remarcabile, conjugata
• ∞·0: transformă în ∞/∞ sau 0/0
• 1^∞: aplică formula lim $1 + 1/x$^x = e
• 0^0: folosește e^(g·ln f)

Metode avansate

Criteriul Stolz-Cesaro: lim a_n/b_n = lim $a_n+1 - a_n$/$b_n+1 - b_n$

Criteriul radical: lim √a_n = lim a_n+1/a_n

Criteriul raportului:

• lim a_n+1/a_n = l < 1 ⟹ lim a_n = 0
• lim a_n+1/a_n = l > 1 ⟹ lim a_n = ∞

Criteriul cleștelui: Dacă f(x) ≤ g(x) ≤ h(x) și lim f(x) = lim h(x) = l, atunci lim g(x) = l

Calculul integralelor

Primitive fundamentale

• ∫ x^n dx = x^$n+1$/$n+1$ + C $n ≠ -1$
• ∫ 1/x dx = ln|x| + C
• ∫ e^x dx = e^x + C
• ∫ sin x dx = -cos x + C
• ∫ cos x dx = sin x + C
• ∫ 1/$x^2+a^2$ dx = $1/a$·arctg$x/a$ + C
• ∫ 1/√$a^2-x^2$ dx = arcsin$x/a$ + C

Metode de integrare

1. Integrarea prin părți: ∫ f(x)·g'(x) dx = f(x)·g(x) - ∫ f'(x)·g(x) dx

Pentru integrale definite: ∫[a,b] f(x)·g'(x) dx = [f(x)·g(x)]_a^b - ∫[a,b] f'(x)·g(x) dx

Sfat practic: Alege f(x) astfel încât f'(x) să fie mai simplu decât f(x), și g'(x) astfel încât integrala ∫ f'(x)·g(x) să fie mai ușor de calculat decât integrala inițială.

2. Schimbarea de variabilă: ∫ f(u(x))·u'(x) dx = ∫ f(t) dt $unde t = u(x)$

3. Integrarea funcțiilor raționale:

• Pentru fracții simple de forma A/$x-a$^n
• Pentru fracții de forma $Ax+B$/$ax^2+bx+c$^n

4. Descompunerea în fracții simple:

1. Împarți P(x) la Q(x) când grad P ≥ grad Q
2. Descompui Q(x) în factori ireductibili
3. Separi fracția în funcție de factorii lui Q(x)
4. Aduci la același numitor și compari coeficienții
5. Rezolvi sistemul pentru a găsi coeficienții fracțiilor simple

5. Integrarea unor expresii speciale:

• Pentru ∫ R(tg x) dx: folosește substituția t = tg x
• Pentru ∫ R(sin x, cos x) dx: folosește formule de reducere
• Pentru ∫ sin^m x cos^n x dx: separă în funcție de paritatea lui m și n

Proprietățile integralei definite și polinoame

Proprietățile integralei definite

Proprietăți algebrice:

• Liniaritate: ∫[a,b] $αf(x) + βg(x)$ dx = α∫[a,b] f(x) dx + β∫[a,b] g(x) dx
• Aditivitate: ∫[a,b] f(x) dx = ∫[a,c] f(x) dx + ∫[c,b] f(x) dx

Proprietăți de comparare:

• Monotonie: Dacă f(x) ≤ g(x), atunci ∫[a,b] f(x) dx ≤ ∫[a,b] g(x) dx
• Mărginire: m$b-a$ ≤ ∫[a,b] f(x) dx ≤ M$b-a$ (unde m ≤ f(x) ≤ M)

Integrabilitate:

• Funcții continue pe [a,b] sunt integrabile
• Funcții monotone pe [a,b] sunt integrabile
• Modificarea unei funcții în puncte izolate nu afectează integrala

Important! Teorema valorii medii pentru integrale: Pentru orice funcție continuă f pe [a,b], există c∈[a,b] astfel încât ∫[a,b] f(x) dx = f(c)$b-a$.

Aplicații:

• Aria suprafeței: A = ∫[a,b] |f(x)| dx sau A = ∫[a,b] |f(x) - g(x)| dx
• Volumul corpurilor de rotație: V = π∫[a,b] [f(x)]² dx

Polinoame

Proprietăți:

• Suma coeficienților: f(1)
• Suma coeficienților de rang par: $f(1) + f(-1)$/2
• Suma coeficienților de rang impar: $f(1) - f(-1)$/2
• Coeficienți individuali: a₀ = f(0), a₁ = f'(0)/1!, a₂ = f''(0)/2!, etc.

Împărțirea polinoamelor:

• Restul împărțirii lui f(x) la x-a este f(a) (teorema restului)
• Schema lui Horner este o metodă eficientă pentru calculul valorii unui polinom într-un punct și pentru împărțirea polinoamelor

Divizibilitatea polinoamelor:

• f : g ⟺ restul = 0
• f(a) = 0 ⟺ f este divizibil cu x-a
• f'(a) = 0 ⟺ f este divizibil cu $x-a$²