Formule Esențiale pentru Bacalaureat

Logaritmi

Logaritmul reprezintă operația inversă a ridicării la putere. Dacă a^x = N, atunci x = log_a N, unde a > 0, a ≠ 1 și N > 0. Pentru a exista un logaritm, trebuie respectate trei condiții: baza să fie pozitivă, diferită de 1, iar cantitatea (numărul din care luăm logaritm) trebuie să fie pozitivă.

Există două tipuri speciale de logaritmi pe care îi vei folosi frecvent: logaritmul zecimal (lg x = log₁₀ x) și logaritmul natural (ln x = log_e x, unde e ≈ 2,71).

Proprietățile logaritmilor te ajută să simplifici calcule complexe:

• log_a 1 = 0 și log_a a = 1
• log_a x^n = n · log_a x
• log_a (x·y) = log_a x + log_a y
• log_a (x/y) = log_a x - log_a y
• log_a b = log_c b / log_c a (formula de schimbare a bazei)

De reținut! Funcțiile logaritmice și exponențiale au comportamente de monotonie opuse: când baza a ∈ (0,1), funcția logaritmică este strict descrescătoare, iar când a > 1, este strict crescătoare.

Puteri și radicali

Puterile sunt operații matematice unde un număr (baza) este înmulțit cu sine de un anumit număr de ori (exponentul). Pentru a^n, a este baza, iar n este exponentul.

Proprietățile puterilor te ajută să simplifici expresii complexe:

• a^0 = 1 (orice număr la puterea zero este 1)
• a^n · a^m = a^$n+m$ (înmulțirea puterilor cu aceeași bază)
• a^n / a^m = a^$n-m$ (împărțirea puterilor cu aceeași bază)
• $a^n$^m = a^(n·m) (puterea unei puteri)
• a^$-n$ = 1/a^n (puterea negativă)

Radicalii reprezintă operația inversă a ridicării la putere. √a este rădăcina de ordin 2 a lui a, iar ∛a este rădăcina de ordin 3.

Pentru radicalii de ordin par (cum ar fi rădăcina pătrată), expresia de sub radical trebuie să fie pozitivă sau zero. Pentru radicalii de ordin impar (cum ar fi rădăcina cubică), nu există această restricție.

Important! Reține că radicalii pot fi scriși ca puteri cu exponent fracționar: √x = x^$1/2$, ∛x = x^$1/3$, și în general √^n x = x^$1/n$, ceea ce îți permite să folosești proprietățile puterilor pentru simplificarea expresiilor cu radicali.

Numere complexe - forma algebrică

Numerele complexe extind sistemul numeric real și se scriu în forma algebrică z = a + bi, unde a și b sunt numere reale, iar i este unitatea imaginară cu proprietatea i² = -1.

În orice număr complex z = a + bi:

• a = Re$z$ reprezintă partea reală
• b = Im$z$ reprezintă partea imaginară

Două numere complexe sunt egale $a₁ + b₁i = a₂ + b₂i$ dacă și numai dacă a₁ = a₂ și b₁ = b₂.

Conjugatul unui număr complex z = a + bi este z̄ = a - bi, iar modulul său se calculează cu formula |z| = √$a² + b²$.

Proprietățile modulului și conjugatului te ajută la simplificarea calculelor:

• |z| = |z̄|
• |z₁·z₂| = |z₁|·|z₂|
• z∈ℝ ⟺ z = z̄
• |z|² = z·z̄

Reține! Pentru puterile lui i există un model repetitiv: i¹ = i, i² = -1, i³ = -i, i⁴ = 1, după care ciclul se repetă. Astfel, poți calcula orice putere a lui i folosind restul împărțirii exponentului la 4.

Formule de calcul prescurtat și concepte fundamentale

Formulele de calcul prescurtat sunt esențiale pentru simplificarea expresiilor algebrice:

• $a + b$² = a² + 2ab + b²
• $a - b$² = a² - 2ab + b²
• a² - b² = a - b$$a + b
• a³ - b³ = a - b$$a² + ab + b²
• a³ + b³ = a + b$$a² - ab + b²

Partea întreagă și fracționară a unui număr real x:

• [x] reprezintă cel mai mare număr întreg mai mic sau egal cu x
• {x} reprezintă diferența x - [x], adică partea fracționară

Proprietăți importante: x = [x] + {x}, partea fracționară este întotdeauna între 0 și 1, iar {x + n} = {x} pentru orice n întreg.

Modulul unui număr real |x| reprezintă distanța de la x la 0 pe axa numerelor: |x| = x pentru x ≥ 0 și |x| = -x pentru x < 0

Sfat util! Inegalitățile cu modul pot fi reformulate: |x| ≤ A înseamnă că -A ≤ x ≤ A, iar |x| ≥ A înseamnă că x ≤ -A sau x ≥ A. Acest lucru te ajută să rezolvi rapid ecuații și inecuații cu modul.

Funcții - definiții și proprietăți

O funcție f: A → B stabilește o corespondență între elementele mulțimii A (domeniul funcției) și elementele mulțimii B (codomeniul), astfel încât fiecărui element din A îi corespunde exact un element din B.

Reprezentarea grafică a funcției (Gf) este formată din toate punctele de coordonate (x, f$x$) din planul xOy, unde x∈A.

Pentru a găsi intersecția graficului cu axele de coordonate:

• Cu axa Ox: rezolvi ecuația f$x$ = 0
• Cu axa Oy: calculezi valoarea f(0)

Când lucrezi cu două funcții, f și g, punctele de intersecție ale graficelor lor se găsesc rezolvând ecuația f$x$ = g$x$. După determinarea abscisei, calculezi și ordonata folosind una dintre funcții.

Important pentru practică! Compunerea funcțiilor (f∘g)$x$ = f(g$x$) este o operație frecvent întâlnită în probleme. Pentru a o calcula, înlocuiești x din expresia lui f cu expresia funcției g.

Funcții - tipuri și proprietăți

Funcțiile se clasifică după comportamentul lor față de operații specifice:

Funcții pare și impare: Pentru o mulțime simetrică A:

• O funcție f este pară dacă f$-x$ = f$x$ pentru orice x∈A
• O funcție f este impară dacă f$-x$ = -f$x$ pentru orice x∈A

Funcții periodice: O funcție f este periodică cu perioada T dacă f$x+T$ = f$x$ pentru orice x din domeniu. Cea mai mică perioadă pozitivă se numește perioadă principală.

Imaginea funcției (Im f) reprezintă mulțimea tuturor valorilor pe care le ia funcția: Im f = {f$x$ | x∈A}.

Proprietăți importante:

• O funcție este injectivă dacă valori diferite din domeniu au imagini diferite
• O funcție este surjectivă dacă orice element din codomeniu este imaginea cel puțin a unui element din domeniu
• O funcție este bijectivă dacă este atât injectivă cât și surjectivă

Sfat practic! Funcțiile strict monotone sunt întotdeauna injective. O funcție este inversabilă dacă și numai dacă este bijectivă. Inversa funcției f, notată f⁻¹, are proprietatea că f(f⁻¹$x$) = x și f⁻¹(f$x$) = x.

Funcția de gradul I

Funcția de gradul I are forma f$x$ = ax + b, unde a și b sunt numere reale, iar a ≠ 0. Reprezentarea sa grafică este o dreaptă.

Monotonia funcției depinde de valoarea lui a:

• Dacă a > 0, funcția este strict crescătoare
• Dacă a < 0, funcția este strict descrescătoare

Pentru a determina semnul funcției, rezolvi ecuația f$x$ = 0, care dă x = -b/a. Apoi analizezi comportamentul funcției:

Aplicații practice: Funcția de gradul I este esențială pentru modelarea multor fenomene din viața reală, cum ar fi costurile, distanțele și alte relații liniare. De asemenea, este baza pentru rezolvarea sistemelor de ecuații liniare, care apar frecvent în probleme practice.

Funcția de gradul al II-lea

Funcția de gradul al II-lea are forma f$x$ = ax² + bx + c, unde a, b, c sunt numere reale și a ≠ 0. Graficul său este o parabolă.

Pentru ecuația asociată ax² + bx + c = 0, calculăm discriminantul Δ = b² - 4ac și analizăm:

• Dacă Δ > 0: ecuația are două soluții reale distincte x₁ = $-b-√Δ$/2a și x₂ = $-b+√Δ$/2a
• Dacă Δ = 0: ecuația are două soluții reale egale x₁ = x₂ = -b/2a
• Dacă Δ < 0: ecuația nu are soluții reale

Semnul funcției depinde de semnul lui a și de valorile rădăcinilor (dacă există).

Relațiile lui Viète pentru rădăcinile x₁ și x₂ sunt:

• Suma rădăcinilor: S = x₁ + x₂ = -b/a
• Produsul rădăcinilor: P = x₁·x₂ = c/a

Trucul rezolvării! Pentru a forma o ecuație de gradul al doilea cu rădăcinile x₁ și x₂ date, calculezi S și P, apoi scrii ecuația în forma x² - Sx + P = 0. Acest procedeu este foarte util în probleme de concurs.

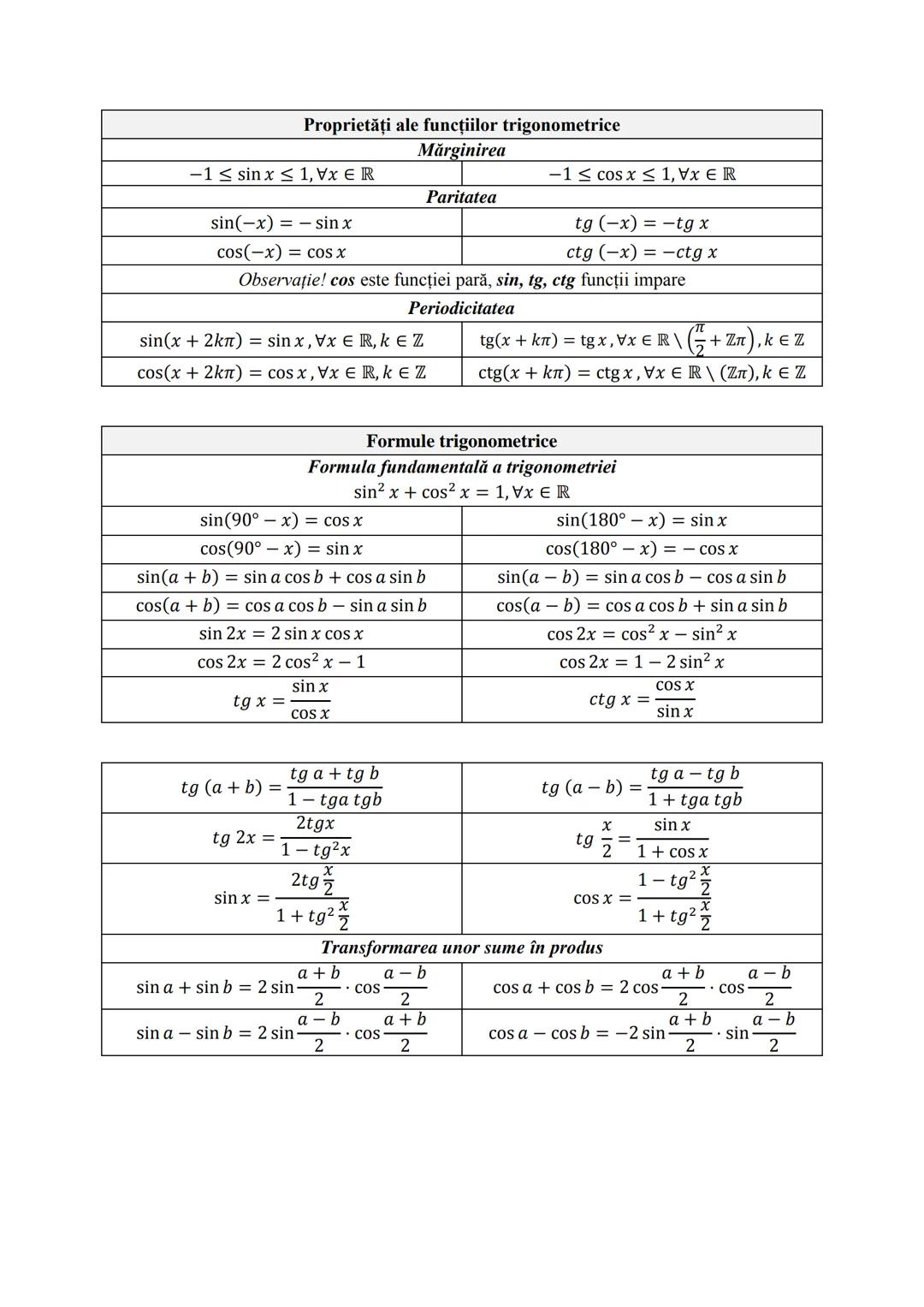
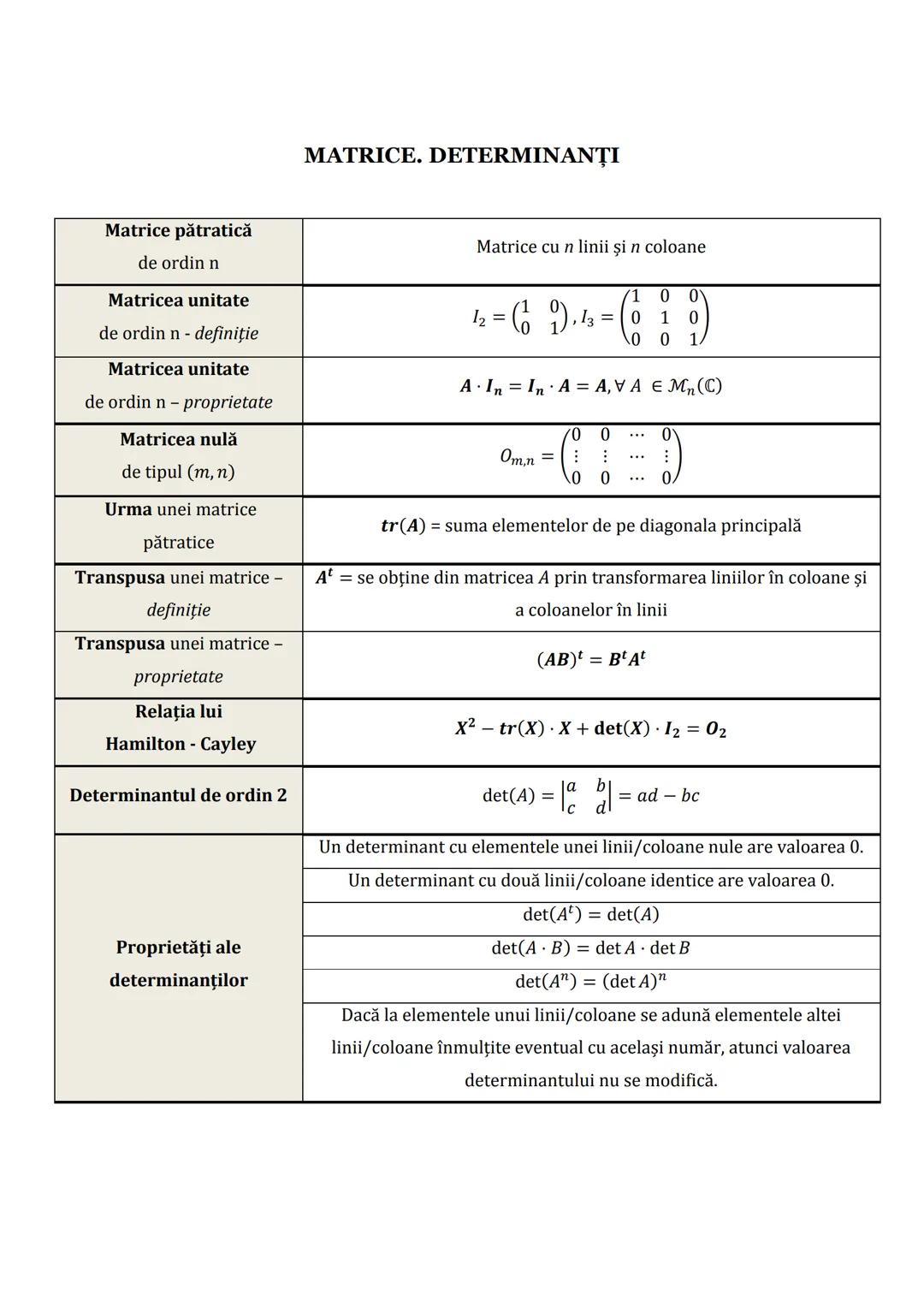
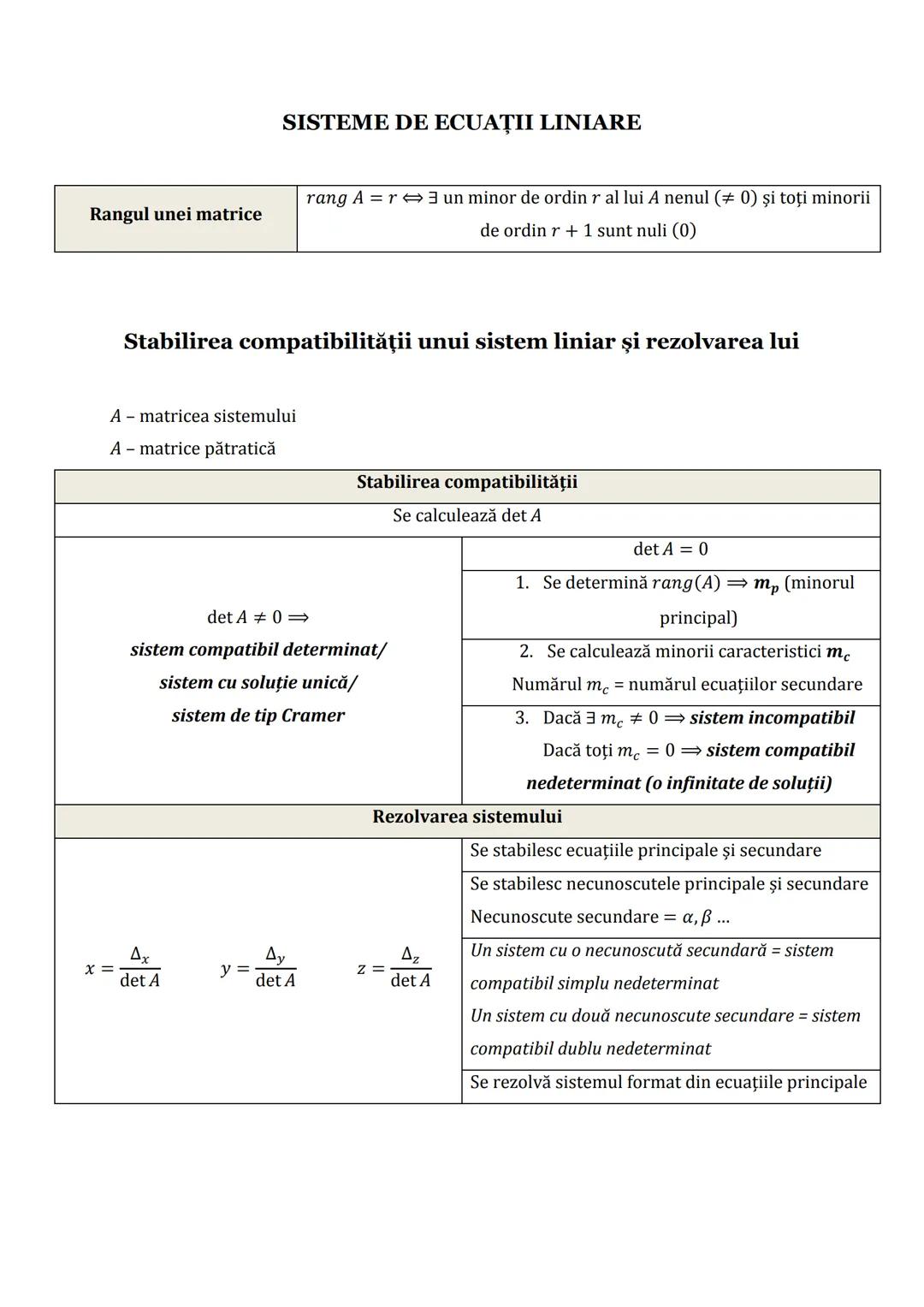
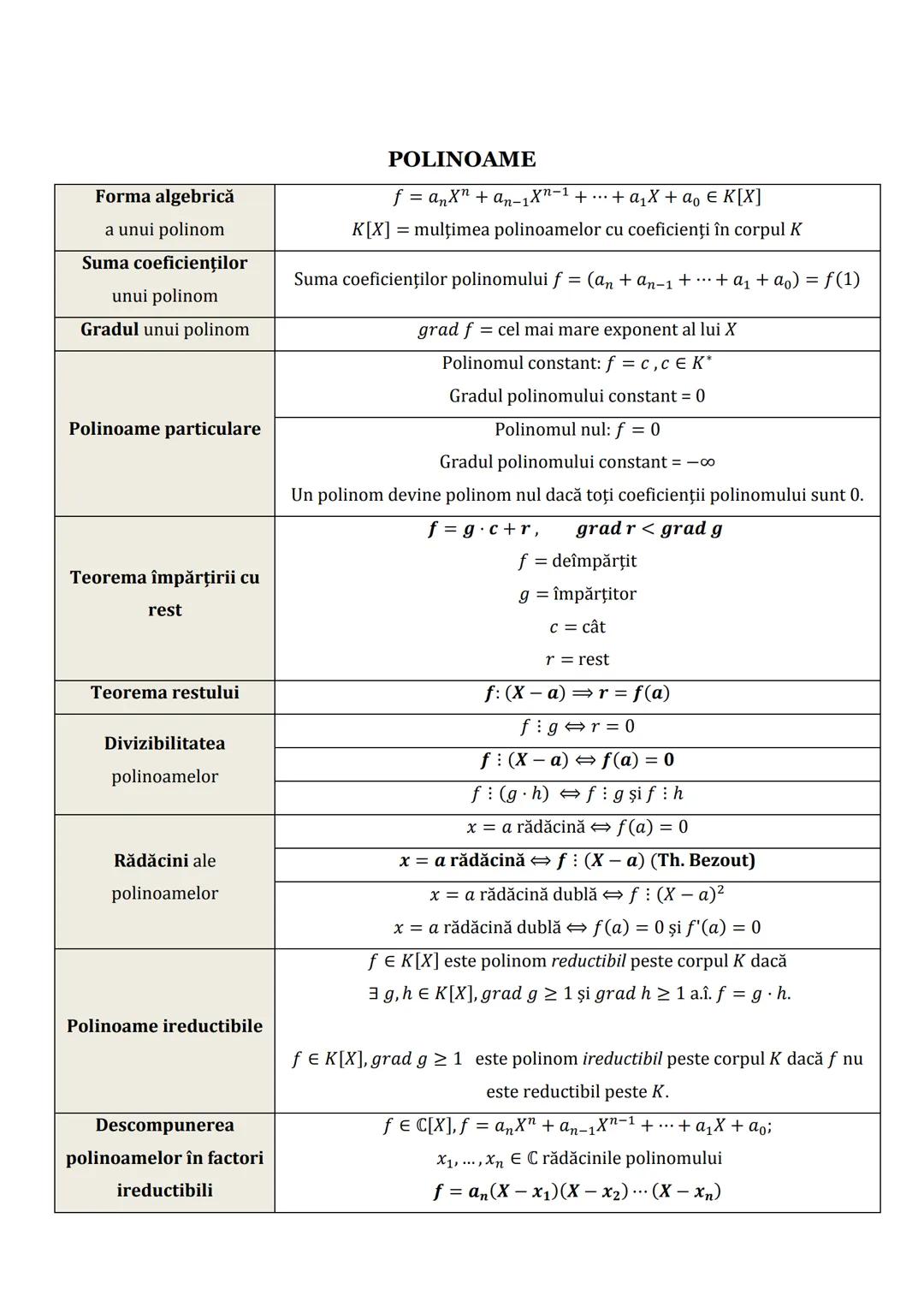
Graficul funcției de gradul al II-lea

Parabola, graficul funcției de gradul al II-lea, are un punct extrem numit vârf (V), cu coordonatele: V$-b/2a, -Δ/4a$

Comportamentul funcției depinde de semnul lui a:

• Dacă a < 0, V este punct de maxim și funcția atinge valoarea maximă f_max = -Δ/4a
• Dacă a > 0, V este punct de minim și funcția atinge valoarea minimă f_min = -Δ/4a

Axa de simetrie a parabolei are ecuația x = -b/2a, fiind paralelă cu axa Oy și trecând prin vârful parabolei.

Poziția parabolei față de axa Ox depinde de discriminantul Δ:

• Dacă Δ > 0: parabola intersectează axa Ox în două puncte distincte
• Dacă Δ = 0: parabola este tangentă la axa Ox (o atinge într-un singur punct)
• Dacă Δ < 0: parabola nu intersectează axa Ox

Vizualizează! Imaginea (domeniul de valori) funcției depinde de vârf: pentru a < 0, Im f = (-∞, -Δ/4a], iar pentru a > 0, Im f = [-Δ/4a, +∞). Monotonia funcției se schimbă la vârf, fiind crescătoare pe o parte și descrescătoare pe cealaltă.

Ecuații speciale

Ecuațiile iraționale conțin necunoscuta sub radical:

• Pentru √f$x$ = g$x$, impunem condițiile f$x$ ≥ 0 și g$x$ ≥ 0
• Pentru ³√f$x$ = g$x$, nu avem condiții suplimentare pentru f$x$

Metoda de rezolvare implică ridicarea la putere pentru eliminarea radicalului:

• Pentru √f$x$ = g$x$, ridicăm la pătrat: f$x$ = g$x$²
• Pentru ³√f$x$ = g$x$, ridicăm la cub: f$x$ = g$x$³

Ecuațiile exponențiale implică necunoscuta în exponent:

• a^f$x$ = a^g$x$ ⟹ f$x$ = g$x$, pentru orice a > 0, a ≠ 1
• a^f$x$ = b ⟹ f$x$ = log_a b

Ecuațiile logaritmice implică necunoscuta în argumentul logaritmului:

• log_a f$x$ = log_a g$x$ ⟹ f$x$ = g$x$, cu condiția f$x$ > 0 și g$x$ > 0
• log_a f$x$ = N ⟹ f$x$ = a^N, cu condiția f$x$ > 0

Atenție! La ecuațiile iraționale și logaritmice este obligatorie verificarea soluțiilor, deoarece prin ridicare la putere sau prin alte transformări pot apărea soluții străine care nu satisfac ecuația inițială.