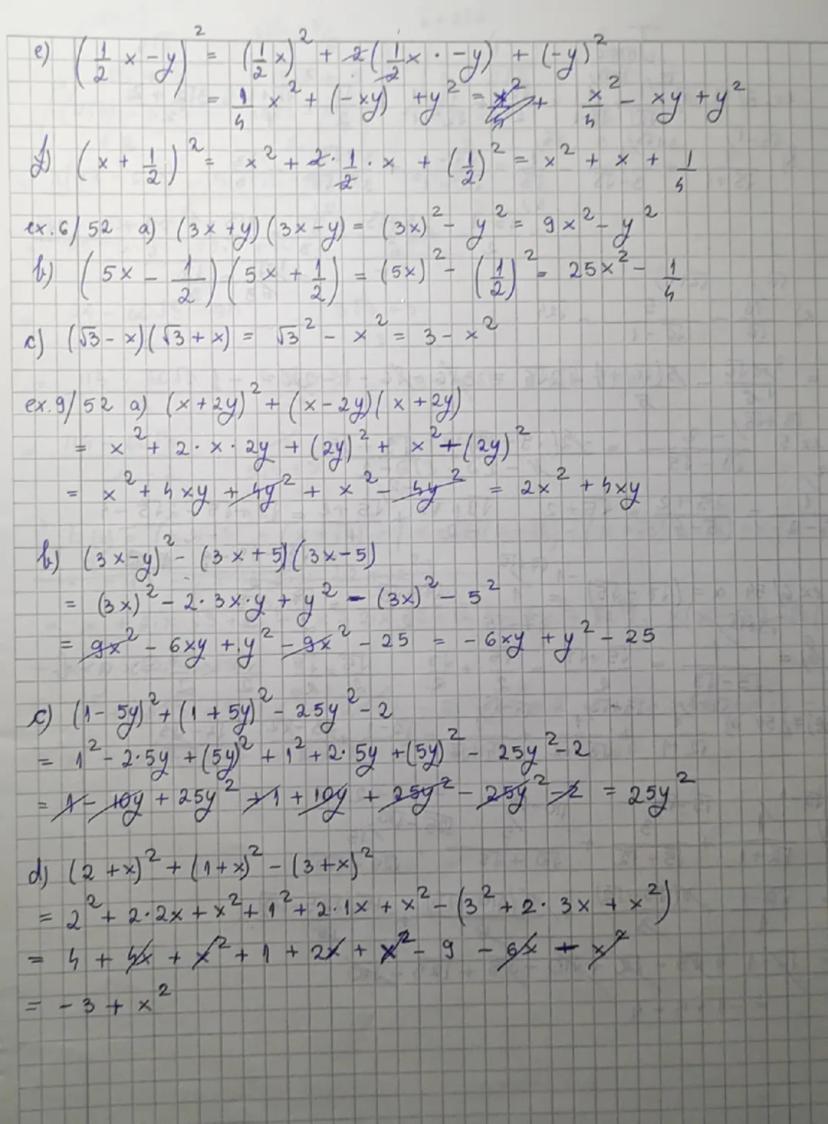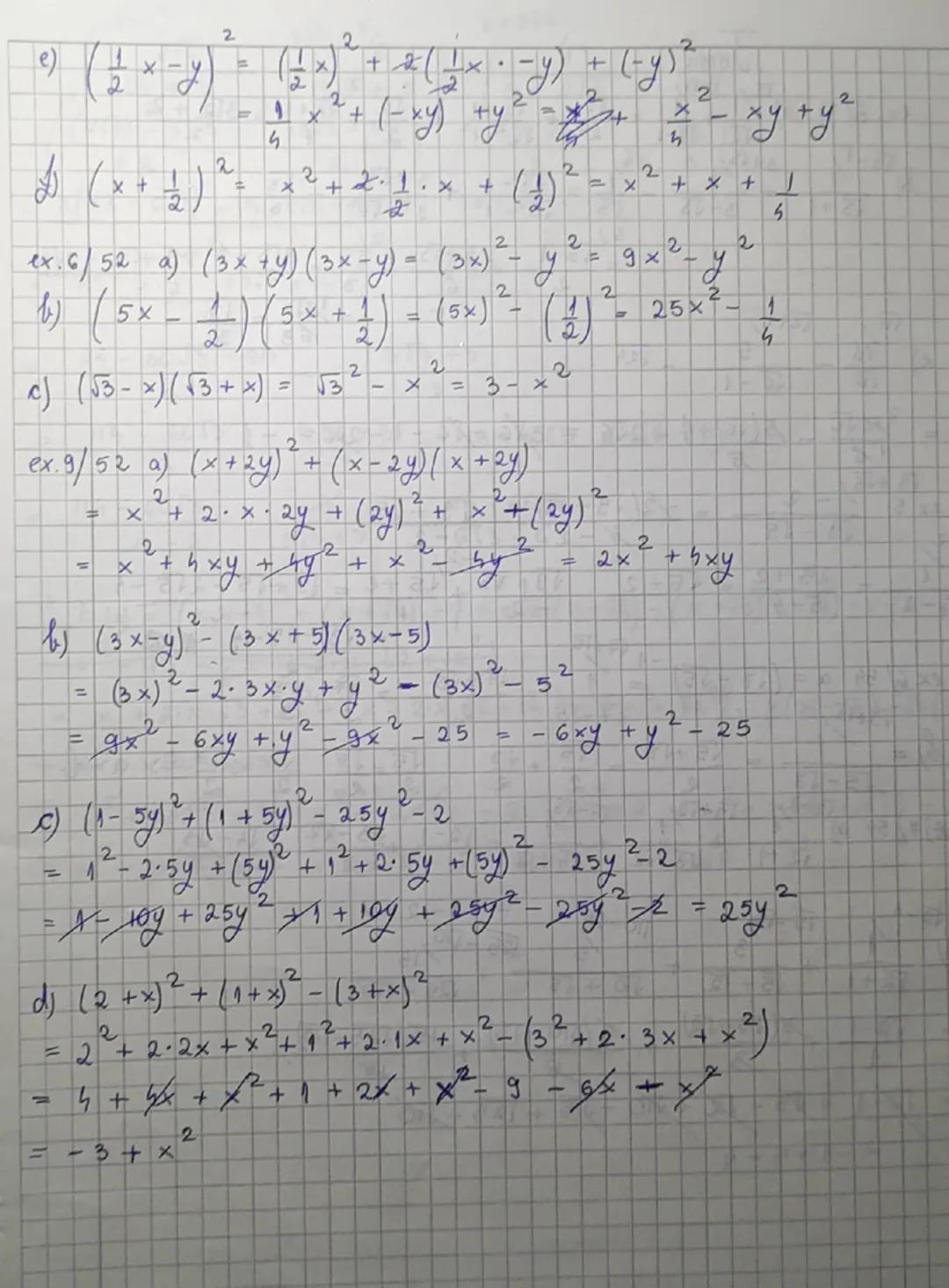Matematică207Actualizat 6 oct. 20264 pagini

Formule de calcul prescurtat simplificate

Reportează

Alexia@alexia_x7ua4

Hei! Te aventurezi prin lumea fascinantă a calculelor algebrice? În aceste note de studiu vom explora înmulțirea unor expresii algebrice și operații cu radicali. Aceste tehnici îți vor fi super utile la matematică și la multe alte discipline.

Înscrie-te pentru a vedea CONȚINUTUL.
E gratuit!

Prin înregistrare, accepți Termenii de serviciu și Politica de confidențialitate

Produse Remarcabile și Calcule Algebrice

Când lucrezi cu expresii precum $(a+b)^2$ sau $(a-b)(a+b)$ , folosești de fapt produse remarcabile. Aceste formule îți economisesc mult timp la rezolvarea exercițiilor.

La înmulțirea expresiilor de tip $(a+b)(a-b)$ obții $a^2-b^2$ , cum se vede în exemplul $(3x+y)(3x-y)=9x^2-y^2$ . Aceasta este formula diferenței de pătrate și e super utilă!

Pentru pătratul unei sume $(a+b)^2=a^2+2ab+b^2$ , observă cum funcționează în $(x+\frac{1}{2})^2=x^2+x+\frac{1}{4}$ . Similar, pentru pătratul unei diferențe $(a-b)^2=a^2-2ab+b^2$ , ca în exemplul $(\frac{1}{2}x-y)^2=\frac{x^2}{4}-xy+y^2$ .

💡 Sfat util: Când combini mai multe expresii algebrice, descompune-le întâi folosind produsele remarcabile, apoi grupează termenii asemenea. Vei vedea că multe termeni se simplifică între ei!

La exercițiile mai complexe precum $(x+2y)^2+(x-2y)(x+2y)$ , aplică formulele pe rând și combină rezultatele. Acest exemplu se simplifica frumos la $2x^2+4xy$ , demonstrând puterea formulelor algebrice.

Înscrie-te pentru a vedea CONȚINUTUL.
E gratuit!

Prin înregistrare, accepți Termenii de serviciu și Politica de confidențialitate

Operații cu Radicali

Când lucrezi cu radicali (expresii cu rădăcini pătrate), trucul principal este raționalizarea numitorului. Acest proces elimină radicalii din numitor și simplifică expresiile.

Pentru a raționaliza un numitor care conține un radical, înmulțești atât numărătorul cât și numitorul cu expresia conjugată a numitorului. De exemplu, pentru $\frac{\sqrt{2}}{\sqrt{2}+1}$ , înmulțești cu $\frac{\sqrt{2}-1}{\sqrt{2}-1}$ și obții o formă mai simplă.

Observă cum se transformă expresiile complexe: $\frac{\sqrt{5}-\sqrt{2}}{\sqrt{5}+\sqrt{2}}$ devine $\frac{7-2\sqrt{10}}{3}$ prin înmulțirea cu conjugata numitorului. Aceste transformări sunt esențiale pentru simplificarea expresiilor iraționale.

🔍 Atenție! La operațiile cu radicali, verifică întotdeauna dacă poți extrage termeni din radical. De exemplu, $\sqrt{24} = 2\sqrt{6}$ deoarece $24 = 4 \cdot 6$ și $\sqrt{4} = 2$ .

Uneori e nevoie să aduni mai multe fracții cu radicali, cum ar fi $\frac{\sqrt{5}-1}{\sqrt{2}+1} + \frac{\sqrt{5}-\sqrt{2}}{3}$ . În aceste cazuri, aduci totul la numitor comun sau folosești tehnici specifice pentru a combina termenii și a obține o expresie finală simplificată.

Înscrie-te pentru a vedea CONȚINUTUL.
E gratuit!

Prin înregistrare, accepți Termenii de serviciu și Politica de confidențialitate

Înscrie-te pentru a vedea CONȚINUTUL.
E gratuit!

Prin înregistrare, accepți Termenii de serviciu și Politica de confidențialitate

Credeam că nu vei întreba niciodată...

Companionul nostru AI este creat special pentru nevoile studenților. Bazându-ne pe milioanele de materiale de pe platformă, putem oferi răspunsuri exacte și relevante pentru studenți. Dar nu este vorba doar despre răspunsuri, companionul este mai ales despre ghidarea studenților prin provocările zilnice de învățare, cu planuri de studiu personalizate, chestionare sau conținuturi în chat și personalizare 100% bazată pe abilitățile și evoluțiile studenților.

Aplicația este disponibilă în Google Play Store și Apple App Store.

Da! Bucură-te de access la materiale de studiu, conectează-te cu alți elevi, și primește ajutor instant - toate acestea la un click distanță. În plus, câștigă puncte ca să deblochezi mai multe funcționalități!

Formule de calcul prescurtat simplificate

Produse Remarcabile și Calcule Algebrice

Operații cu Radicali

Credeam că nu vei întreba niciodată...

Ce este Companionul AI Knowunity?

De unde pot descărca aplicația Knowunity?

Este Knowunity chiar gratuită?

Conținut similar

recapitulare pentru evaluarea nationala

Test clasa a8a

Formule Bac Mate

Simulare matematica 2025

Clasificarea termenilor

SUBIECT 1 SIMULARE MATE

Cel mai popular conținut: Adding and Subtracting Rational Expressions

recapitulare pentru evaluarea nationala

Cel mai popular conținut: Matematică

Formule pentru subiectul 1 Bac Mate M2

Teorie Bac Mate

Portofoliu geometrie clasele 5-8

formule bac mate

Formule Bac Matematica

formule matematică pentru bac

exercitii bac mate sub 1

recapitulare pentru evaluarea nationala

Recapitulare EN- algebra clasele 5-8

Cel mai popular conținut

Povestea lui Harap Alb Rezumat BAC

Eseuri Limba si literatura română

Toate eseurile pentru bac

Eseu Povestea lui Harap Alb

Eseu- “Povestea lui Harap-Alb” de Ion Creanga

Lecții Istorie BAC

ESEU PLUMB DE GEORGE BACOVIA

Materie geografie bac

Rezumat Harap Alb

Recenzii de la utilizatorii noștri. Ei iubesc să folosească Knowunity, și tu o vei face.