Progresii - Aritmetice vs. Geometrice

Progresiile sunt șiruri de numere cu reguli precise de formare. Le întâlnești des în matematică, dar și în situații practice precum calculul dobânzilor sau planificarea financiară.

În progresiile aritmetice, diferența dintre termeni consecutivi este constantă. De exemplu, șirul 2, 5, 8, 11... are diferența constantă r = 3. Termenul general se calculează cu formula: a_n = a_1 + $n-1$r.

În progresiile geometrice, raportul dintre termeni consecutivi este constant. De exemplu, șirul 2, 6, 18, 54... are raportul q = 3. Termenul general se calculează cu formula: b_n = b_1 · q^$n-1$.

Sumele primilor n termeni sunt ușor de calculat: pentru progresii aritmetice avem S_n = $a_1 + a_n$ · n/2, iar pentru progresii geometrice S_n = b_1$q^n - 1$/$q - 1$ când q ≠ 1.

💡 Dacă ai trei numere consecutive A, B, C, verifică rapid: în progresie aritmetică 2B = A + C, iar în progresie geometrică B² = A · C!

Logaritmi - Proprietăți și Aplicații

Logaritmii sunt operații inverse ale puterilor și apar frecvent în modelarea fenomenelor din fizică, economie sau știință. Când scrii a^x = N, logaritmul este x = log_a N.

Pentru ca un logaritm să existe, trebuie respectate trei condiții importante: baza trebuie să fie pozitivă și diferită de 1, iar cantitatea trebuie să fie pozitivă. Cele mai folosite tipuri sunt logaritmul zecimal $lg x = log_10 x$ și logaritmul natural $ln x = log_e x$.

Principalele proprietăți ale logaritmilor te vor ajuta să simplifici calcule complicate:

• log_a(x·y) = log_a x + log_a y
• log_a$x/y$ = log_a x - log_a y
• log_a$x^n$ = n·log_a x

Pentru schimbarea bazei, poți folosi formula: log_a b = log_c b / log_c a. Aceasta este utilă când calculezi logaritmi cu baze mai puțin comune.

💡 Funcția logaritmică are comportamente diferite în funcție de bază: dacă a > 1, funcția este strict crescătoare, iar dacă 0 < a < 1, funcția este strict descrescătoare.

Noțiuni Fundamentale despre Funcții

Funcțiile matematice sunt relații care asociază fiecărui element dintr-o mulțime A (domeniul) un singur element dintr-o mulțime B (codomeniul). Ele sunt notate f: A → B, x → f(x).

Când lucrezi cu grafice de funcții, vei avea nevoie să identifici punctele de intersecție cu axele de coordonate. Pentru intersecția cu Ox, rezolvi ecuația f(x) = 0, iar pentru intersecția cu Oy, calculezi valoarea f(0).

Pentru a găsi coordonatele punctelor de intersecție între graficele a două funcții f și g, urmează acești pași simpli:

1. Rezolvă ecuația f(x) = g(x) pentru a determina abscisa (x)
2. Calculează ordonata (y) folosind oricare dintre funcții: y = f(x) = g(x)

La compunerea funcțiilor, ordinea contează: (f∘g)(x) = f(g(x)). Acest concept este esențial în rezolvarea unor probleme complexe.

💡 Funcțiile sunt unele dintre cele mai versatile instrumente matematice, permițându-ți să modelezi diverse fenomene din lumea reală!

Funcții - Clasificare și Proprietăți

Funcțiile pot fi clasificate după mai multe criterii, fiecare tip având proprietăți specifice care te ajută să le analizezi comportamentul.

O funcție f este pară dacă f$-x$ = f(x) pentru orice x din domeniu. Graficul unei astfel de funcții este simetric față de axa Oy. De exemplu, f(x) = x² este o funcție pară.

O funcție f este impară dacă f$-x$ = -f(x) pentru orice x din domeniu. Graficul unei astfel de funcții este simetric față de origine. De exemplu, f(x) = x³ este o funcție impară.

Funcțiile periodice repetă valorile la intervale regulate: f$x+T$ = f(x). Funcțiile trigonometrice sunt exemple clasice de funcții periodice.

În privința injectivității și surjectivității:

• O funcție este injectivă dacă valori diferite din domeniu produc valori diferite în codomeniu
• O funcție este surjectivă dacă fiecare element din codomeniu este imaginea cel puțin a unui element din domeniu
• O funcție este bijectivă dacă este atât injectivă cât și surjectivă

💡 Doar funcțiile bijective au inverse! Aceasta este o proprietate esențială în multe aplicații practice.

Funcțiile monotone păstrează sau inversează ordinea elementelor: pot fi crescătoare (f(x₁) ≤ f(x₂) când x₁ < x₂) sau descrescătoare (f(x₁) ≥ f(x₂) când x₁ < x₂). Monotonia strictă adaugă condiția ca valorile să fie diferite.

Funcția de Gradul I

Funcția de gradul I, cunoscută și ca funcție liniară, are forma f(x) = ax + b, unde a și b sunt numere reale, iar a ≠ 0. Aceasta este una dintre cele mai simple și mai utilizate funcții în matematică.

Monotonia funcției de gradul I depinde doar de valoarea coeficientului a:

• Dacă a > 0, funcția este strict crescătoare
• Dacă a < 0, funcția este strict descrescătoare

Pentru a afla semnul funcției, trebuie să rezolvi ecuația f(x) = 0, care are soluția x = -b/a. Această valoare împarte axa reală în două intervale:

• La stânga punctului -b/a, funcția are semn contrar lui a
• La dreapta punctului -b/a, funcția are același semn cu a

💡 Graficul funcției de gradul I este întotdeauna o dreaptă! Această proprietate o face extrem de utilă în modelarea relațiilor liniare din viața reală, cum ar fi costurile fixe plus variabile sau distanța în funcție de timp la viteză constantă.

Funcția de Gradul al II-lea

Funcția de gradul al II-lea, sau funcția pătratică, are forma f(x) = ax² + bx + c, unde a, b și c sunt numere reale, iar a ≠ 0. Graficul acestei funcții este o parabolă.

Pentru a rezolva ecuația de gradul al II-lea ax² + bx + c = 0, calculezi mai întâi discriminantul Δ = b² - 4ac, care determină numărul de soluții:

• Dacă Δ > 0: ecuația are două soluții reale distincte
• Dacă Δ = 0: ecuația are o soluție reală dublă
• Dacă Δ < 0: ecuația nu are soluții reale

Semnul funcției de gradul al II-lea depinde de numărul de soluții ale ecuației asociate. De exemplu, când Δ > 0 și a > 0, funcția este negativă între cele două rădăcini și pozitivă în rest.

Relațiile lui Viete sunt foarte utile pentru a lucra cu rădăcinile ecuației de gradul al II-lea:

• Suma rădăcinilor: x₁ + x₂ = -b/a
• Produsul rădăcinilor: x₁ · x₂ = c/a

💡 Dacă cunoști rădăcinile x₁ și x₂ ale unei ecuații, poți forma direct ecuația de gradul al II-lea folosind formula: x² - $x₁ + x₂$x + x₁·x₂ = 0.

Ecuații Iraționale, Exponențiale și Logaritmice

Ecuațiile iraționale conțin necunoscuta sub radical. Pentru ecuații de forma √f(x) = g(x), trebuie să verifici mai întâi condițiile de existență: f(x) ≥ 0 și, pentru radicali de ordin par, g(x) ≥ 0. După ridicarea la pătrat, verifică întotdeauna soluțiile pentru a elimina rădăcinile străine!

Ecuațiile exponențiale conțin necunoscuta la exponent. Cele mai comune tipuri sunt:

• a^f(x) = a^g(x), care se rezolvă prin egalarea exponenților: f(x) = g(x)
• a^f(x) = b, care se transformă în f(x) = log_a b

Ecuațiile logaritmice conțin necunoscuta în argumentul unui logaritm. Pentru log_a f(x) = log_a g(x), condiția de existență cere ca f(x) > 0, g(x) > 0, a > 0 și a ≠ 1. Soluția este f(x) = g(x), dar trebuie verificată în ecuația inițială.

💡 Atenție la condițiile de existență! Este pasul cel mai important în rezolvarea ecuațiilor iraționale și logaritmice, deoarece omiterea lui poate duce la soluții greșite.

Ecuații Trigonometrice

Ecuațiile trigonometrice te ajută să găsești unghiurile care satisfac anumite condiții. Există câteva tipuri fundamentale care apar frecvent:

Pentru sin x = a, unde a ∈ $-1,1$, soluția generală este x = (-1)^k · arcsin a + kπ, k ∈ ℤ. Pentru cos x = a, unde a ∈ $-1,1$, soluția generală este x = ±arccos a + 2kπ, k ∈ ℤ. Pentru tg x = a, unde a ∈ ℝ, soluția generală este x = arctg a + kπ, k ∈ ℤ.

Ecuațiile de forma sin f(x) = sin g(x) se rezolvă folosind proprietatea: f(x) = (-1)^k · g(x) + kπ, k ∈ ℤ. Similar pentru cos și tg.

Pentru ecuații de forma a·cos x + b·sin x + c = 0, o metodă eficientă este substituția tg$x/2$ = t, care transformă expresiile trigonometrice în expresii algebrice raționale.

💡 Nu uita să verifici și valorile x = $2k+1$π, k ∈ ℤ când folosești substituția tg$x/2$ = t, deoarece aceste valori pot fi pierdute în timpul transformării!

Multe ecuații trigonometrice complexe pot fi rezolvate transformându-le în ecuații algebrice prin utilizarea identităților fundamentale, precum sin²x + cos²x = 1 sau cos 2x = cos²x - sin²x = 2cos²x - 1 = 1 - 2sin²x.

Matematici Financiare

Matematica financiară te ajută să iei decizii economice inteligente, fie că este vorba de investiții, credite sau calcule comerciale.

Procentele sunt esențiale în calcule financiare. Pentru a calcula p% dintr-o valoare x, înmulțești $p/100$ · x. La scumpirea unui produs cu p%, prețul final devine x + $p/100$ · x, iar la reducere, prețul final este x - $p/100$ · x.

Taxa pe valoarea adăugată (TVA) se adaugă peste prețul inițial. Dacă procentul TVA este p%, atunci prețul de vânzare devine p_v = x + $p/100$ · x, unde x este prețul de producție.

În cazul dobânzii simple, suma finală crește linear cu timpul. Dobânda se calculează folosind formula D = S · $r/100$ · n, unde S este suma inițială, r este rata dobânzii (în %) și n este perioada în ani. Suma finală va fi S_finală = S + D.

Pentru dobânda compusă, care se aplică la majoritatea depozitelor bancare, dobânda se adaugă la capital la sfârșitul fiecărei perioade. Suma finală se calculează cu formula S_finală = S · $1 + r/100$^n.

💡 Dobânda compusă crește exponențial în timp, în timp ce dobânda simplă crește liniar. Pentru perioade lungi de timp, diferența dintre ele poate deveni semnificativă!

Geometrie Analitică în Plan

Geometria analitică îți permite să rezolvi probleme geometrice folosind coordonate și ecuații algebrice.

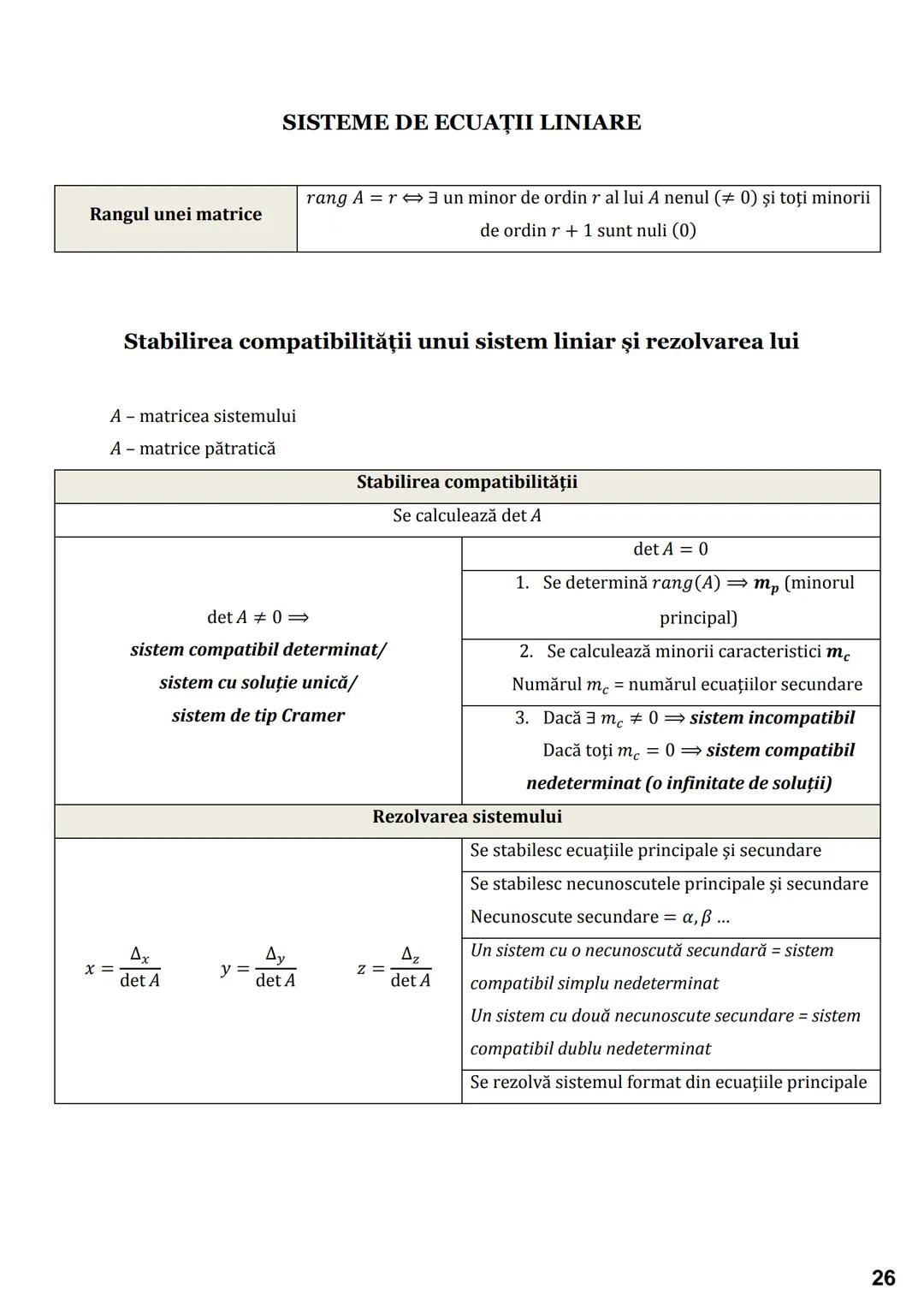
Două drepte d₁ și d₂ pot avea trei poziții relative:

• Sunt paralele când m_d₁ = m_d₂ sau când a₁/a₂ = b₁/b₂ (pentru ecuațiile generale)
• Sunt perpendiculare când m_d₁ · m_d₂ = -1
• Sunt concurente (se intersectează) când a₁/a₂ ≠ b₁/b₂

Aria unui triunghi cu vârfurile A$x_A, y_A$, B$x_B, y_B$ și C$x_C, y_C$ se poate calcula folosind determinantul: A_△ABC = (1/2)|Δ|, unde Δ este determinantul format din coordonatele vârfurilor și coloana de 1.

Trei puncte A, B și C sunt coliniare (se află pe aceeași dreaptă) dacă și numai dacă determinantul format din coordonatele lor este zero.

Distanța de la un punct la o dreaptă A$x_A, y_A$ la dreapta d: ax + by + c = 0 se calculează cu formula: d(A, d) = |ax_A + by_A + c|/√$a² + b²$

Centrul de greutate al unui triunghi ABC are coordonatele: x_G = $x_A + x_B + x_C$/3 și y_G = $y_A + y_B + y_C$/3

💡 Când verifici dacă un punct aparține unei drepte, înlocuiește coordonatele punctului în ecuația dreptei - dacă obții o egalitate adevărată, punctul se află pe dreaptă!