Progresii Aritmetice și Geometrice

Progresiile sunt șiruri de numere care urmează anumite reguli simple. În viața reală, le întâlnești peste tot - de la dobânzi bancare la modele de creștere.

În progresiile aritmetice, diferența dintre termeni consecutivi este constantă (r). Formula de recurență este: $a_{n+1} = a_n + r$. Dacă știi primul termen și rația, poți calcula orice termen folosind formula: $a_n = a_1 + (n-1)r$.

În progresiile geometrice, raportul dintre termeni consecutivi este constant (q). Formula de recurență este: $b_{n+1} = b_n \cdot q$. Formula termenului general este: $b_n = b_1 \cdot q^{n-1}$.

💡 Pont util: Pentru a calcula rapid suma primilor n termeni ai unei progresii aritmetice, folosește formula: $S_n = \frac{(a_1+a_n) \cdot n}{2}$. Pentru progresii geometrice (când q≠1): $S_n = \frac{b_1(q^n-1)}{q-1}$.

O metodă simplă pentru a verifica dacă trei numere sunt în progresie aritmetică este să vezi dacă $2B = A+C$. Pentru progresie geometrică, verifică dacă $B^2 = A \cdot C$.

Numere Complexe - Forma Algebrică

Numerele complexe extind sistemul numerelor reale și sunt esențiale pentru rezolvarea unor probleme care par imposibile în lumea reală.

Un număr complex are forma $z = a + bi$, unde $a$ este partea reală (Re(z)) și $b$ este partea imaginară (Im(z)). Unitatea imaginară $i$ are proprietatea că $i^2 = -1$.

Două numere complexe sunt egale dacă și numai dacă părțile reale sunt egale și părțile imaginare sunt egale: $a_1 + b_1i = a_2 + b_2i \Leftrightarrow a_1 = a_2$ și $b_1 = b_2$.

Conjugatul unui număr complex $z = a + bi$ este $\overline{z} = a - bi$. Această noțiune este foarte utilă în calcule, deoarece $z \cdot \overline{z} = |z|^2 = a^2 + b^2$.

💡 Reține: Pentru a împărți numere complexe, amplifică fracția cu conjugatul numitorului. Astfel transformi totul în formă algebrică standard.

Modulul unui număr complex $z = a + bi$ este $|z| = \sqrt{a^2 + b^2}$. Acesta reprezintă distanța de la originea axelor de coordonate la punctul care reprezintă numărul complex în plan.

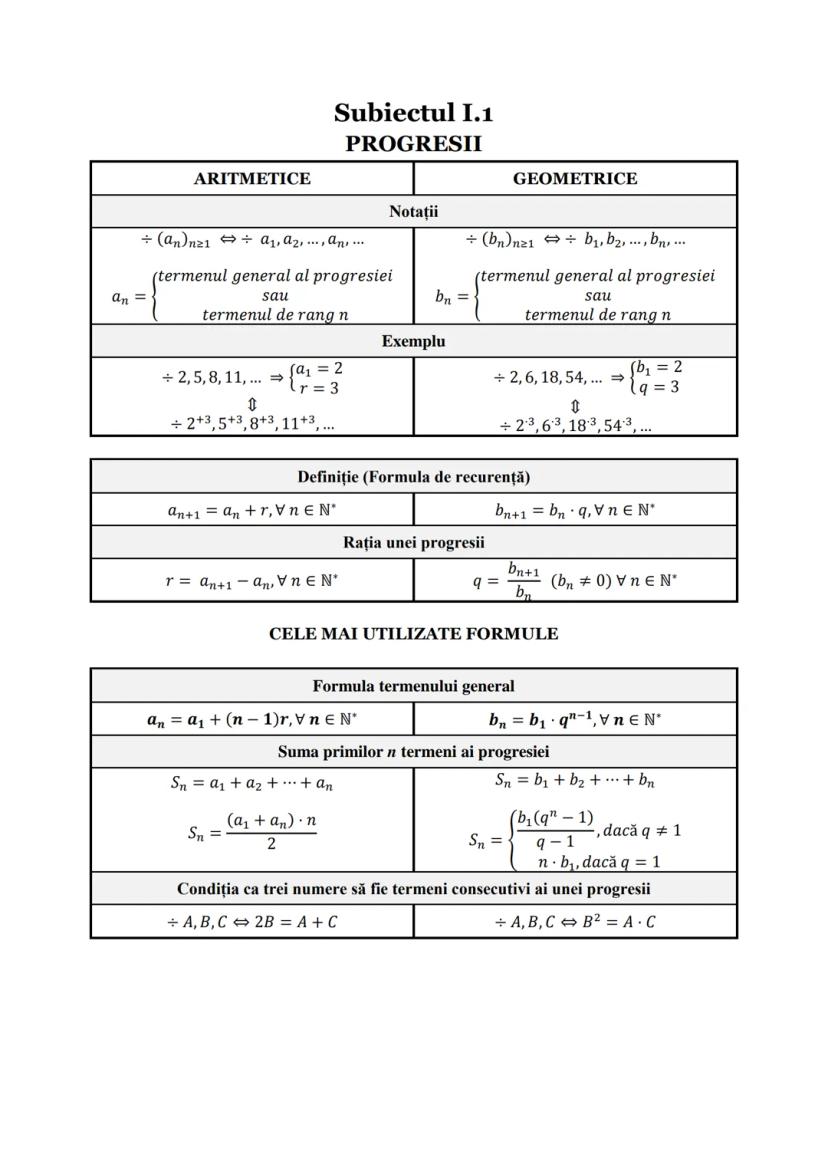
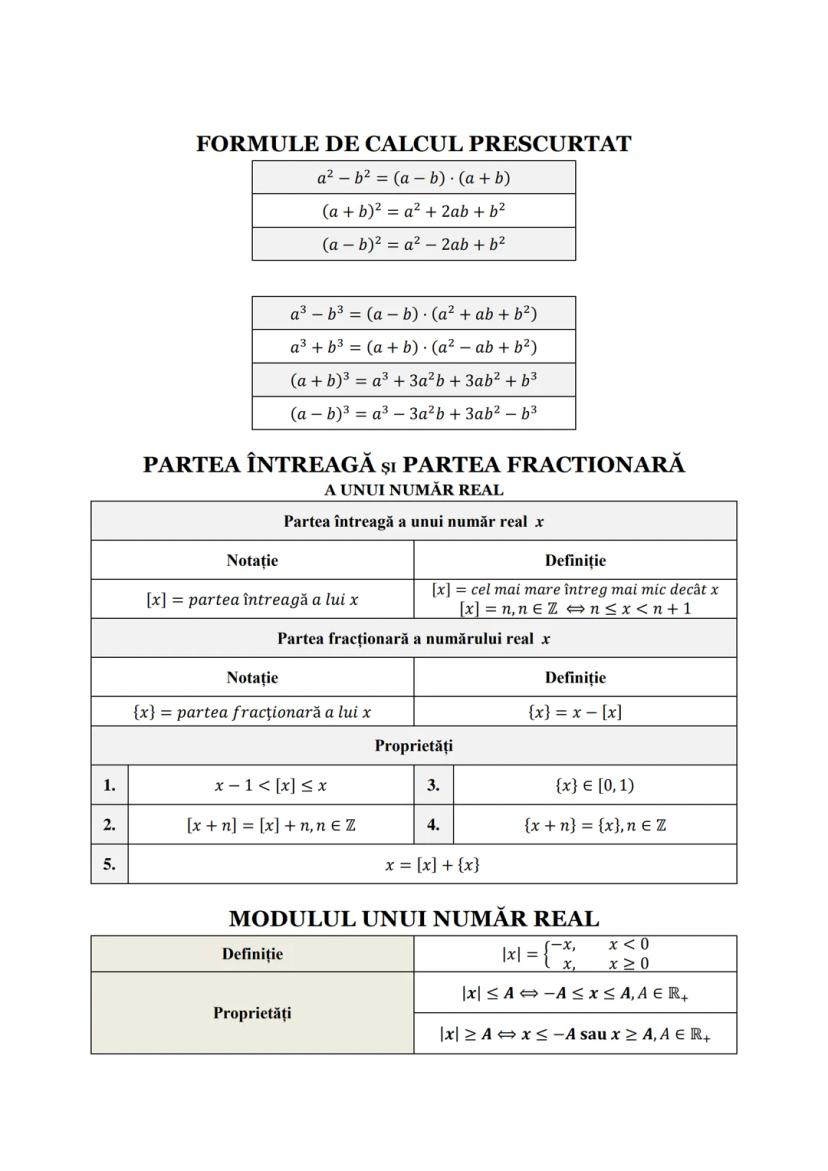
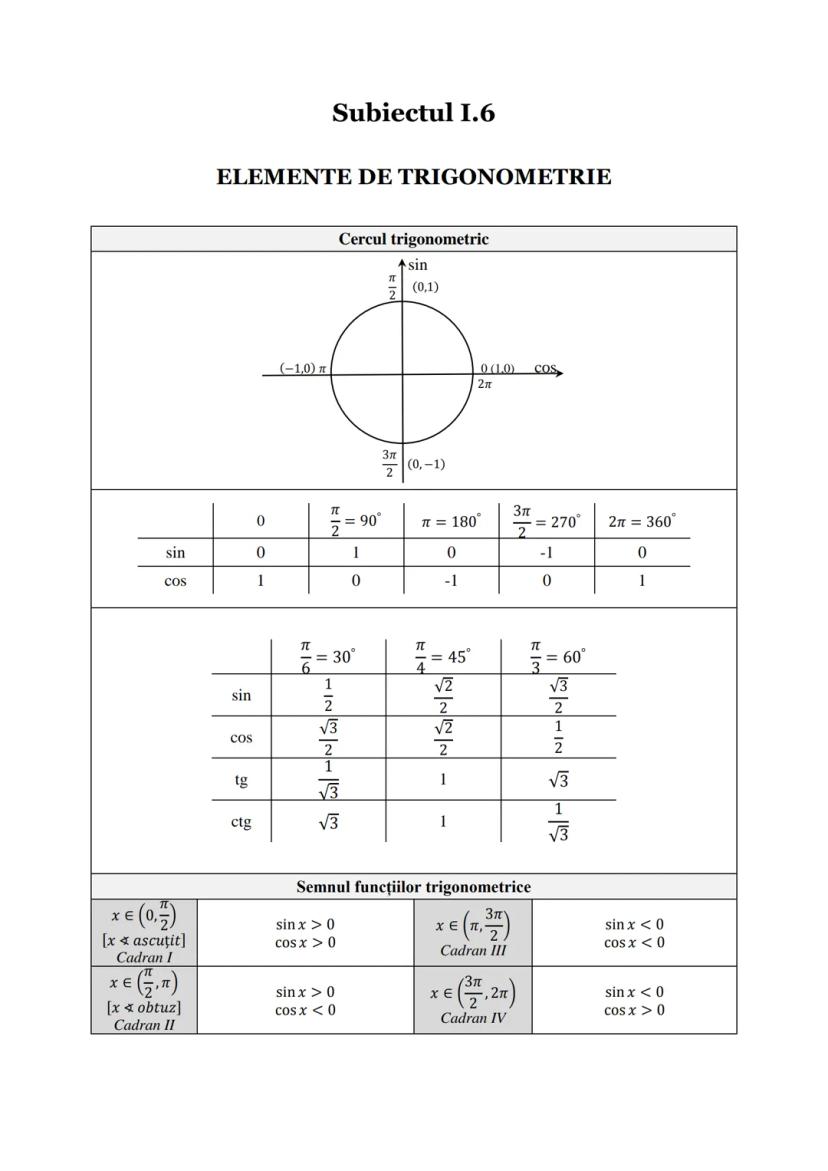
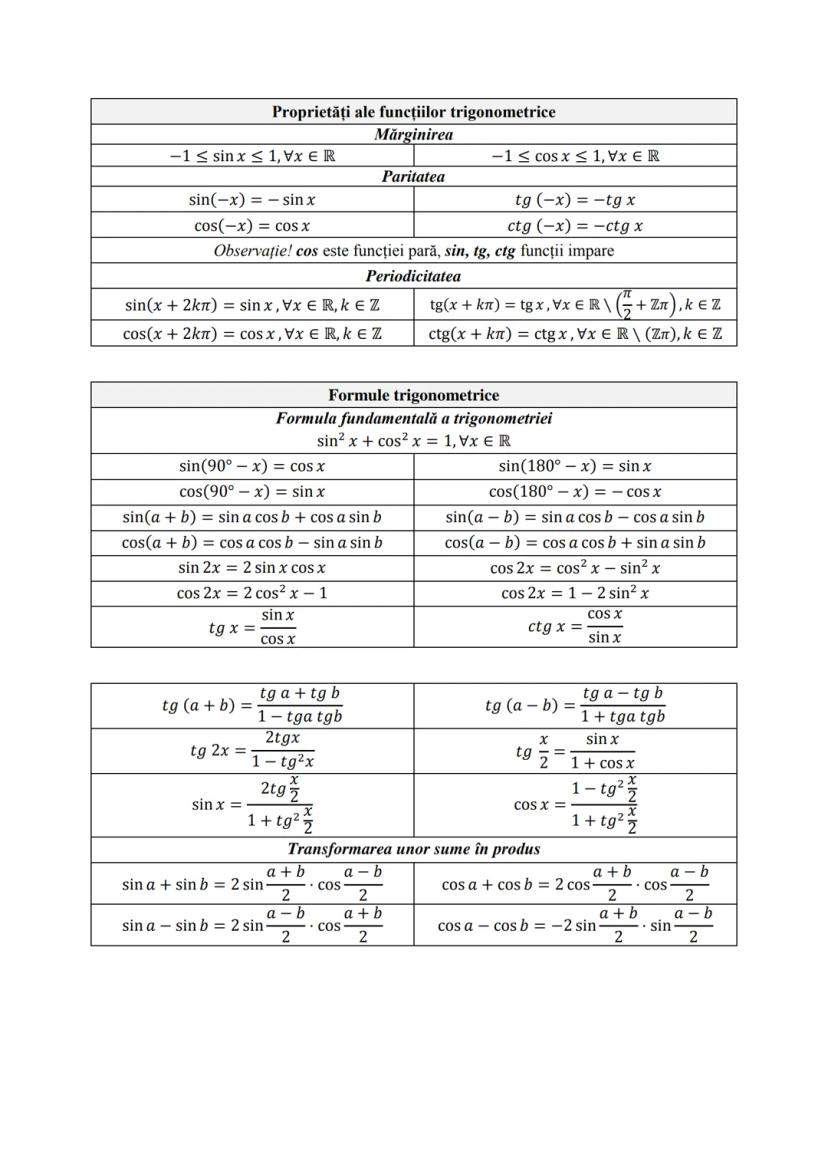
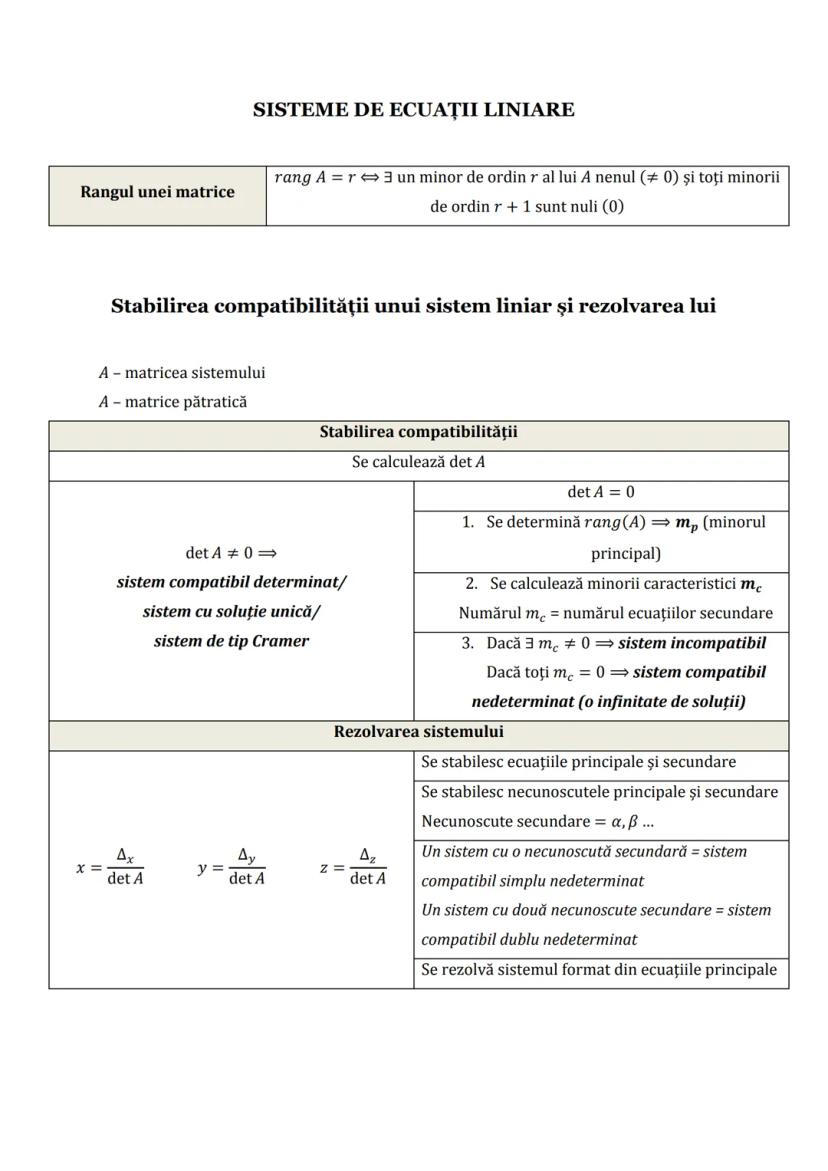
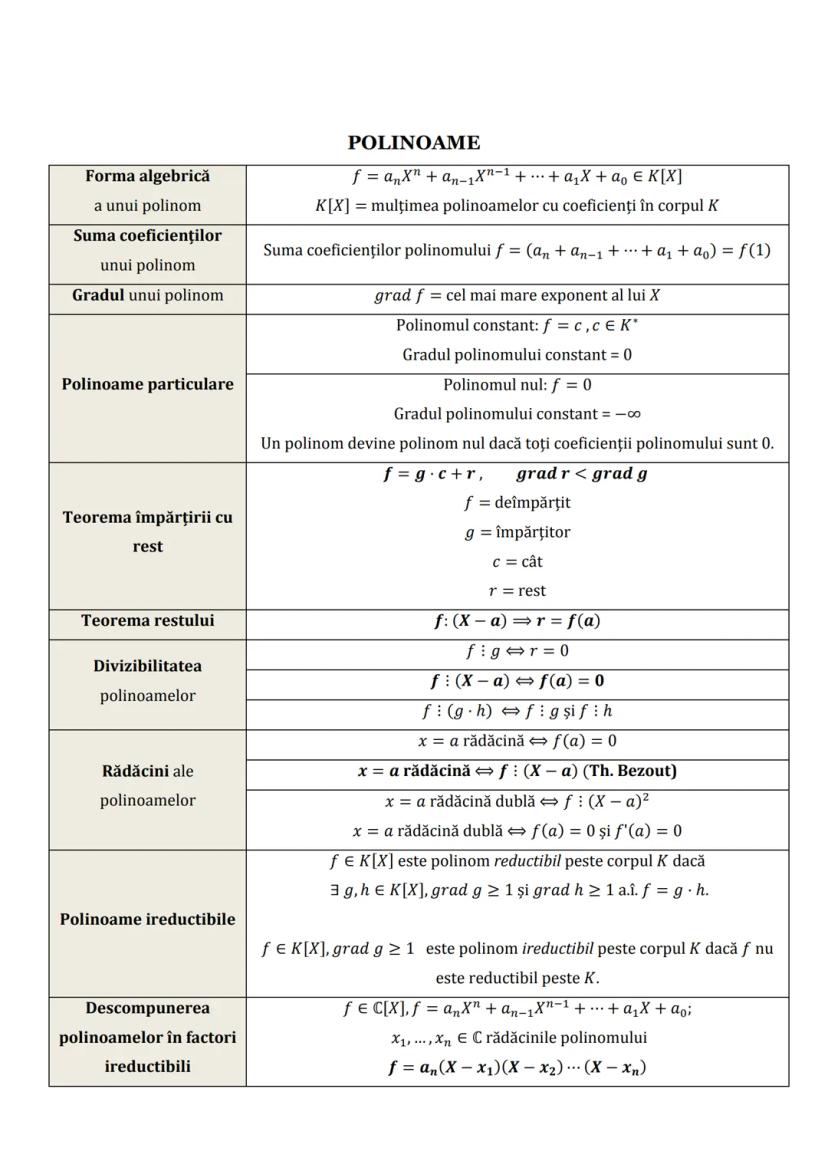
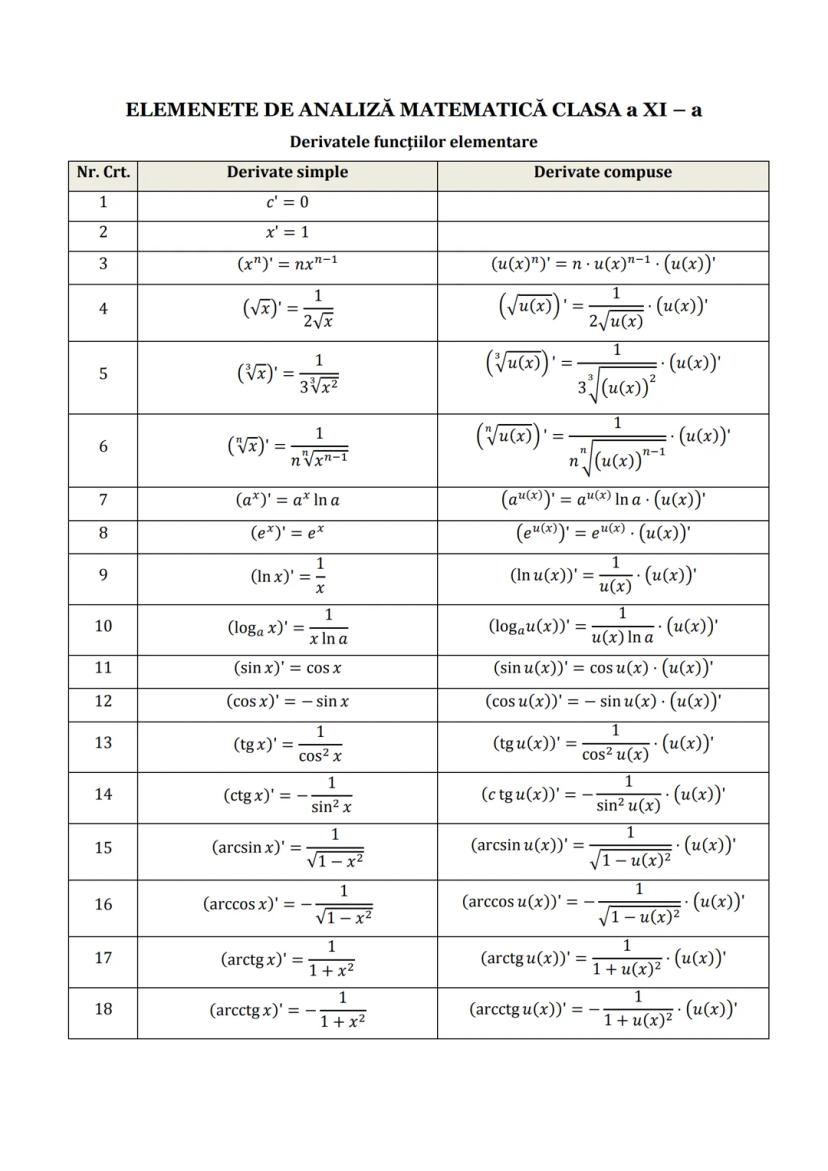
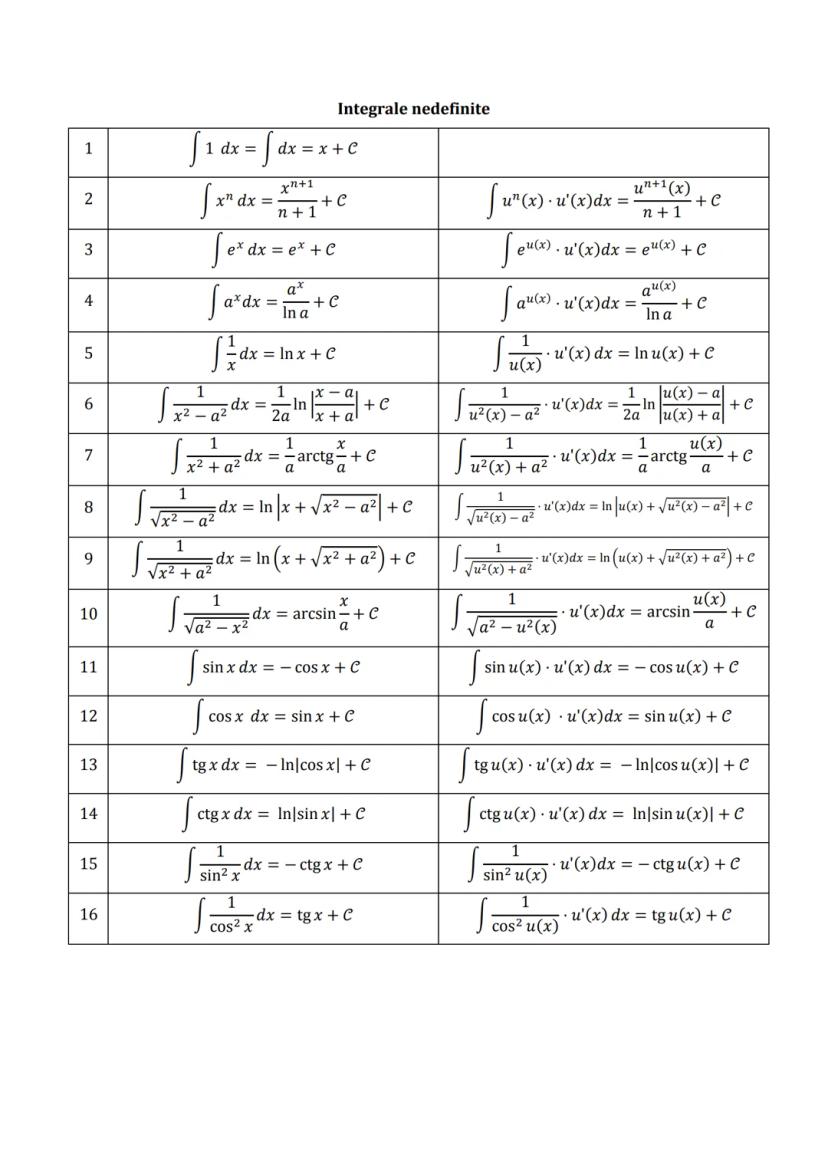
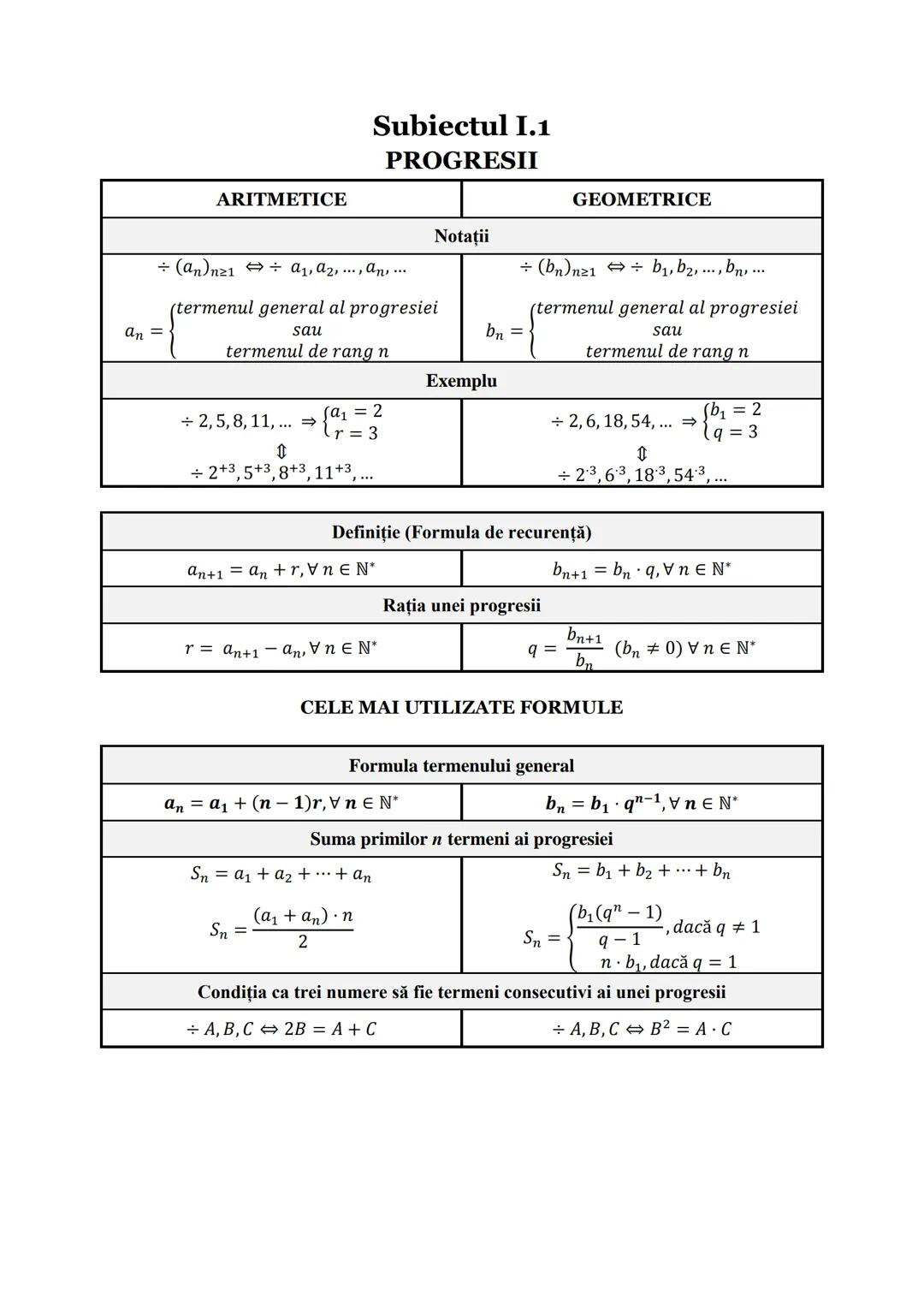
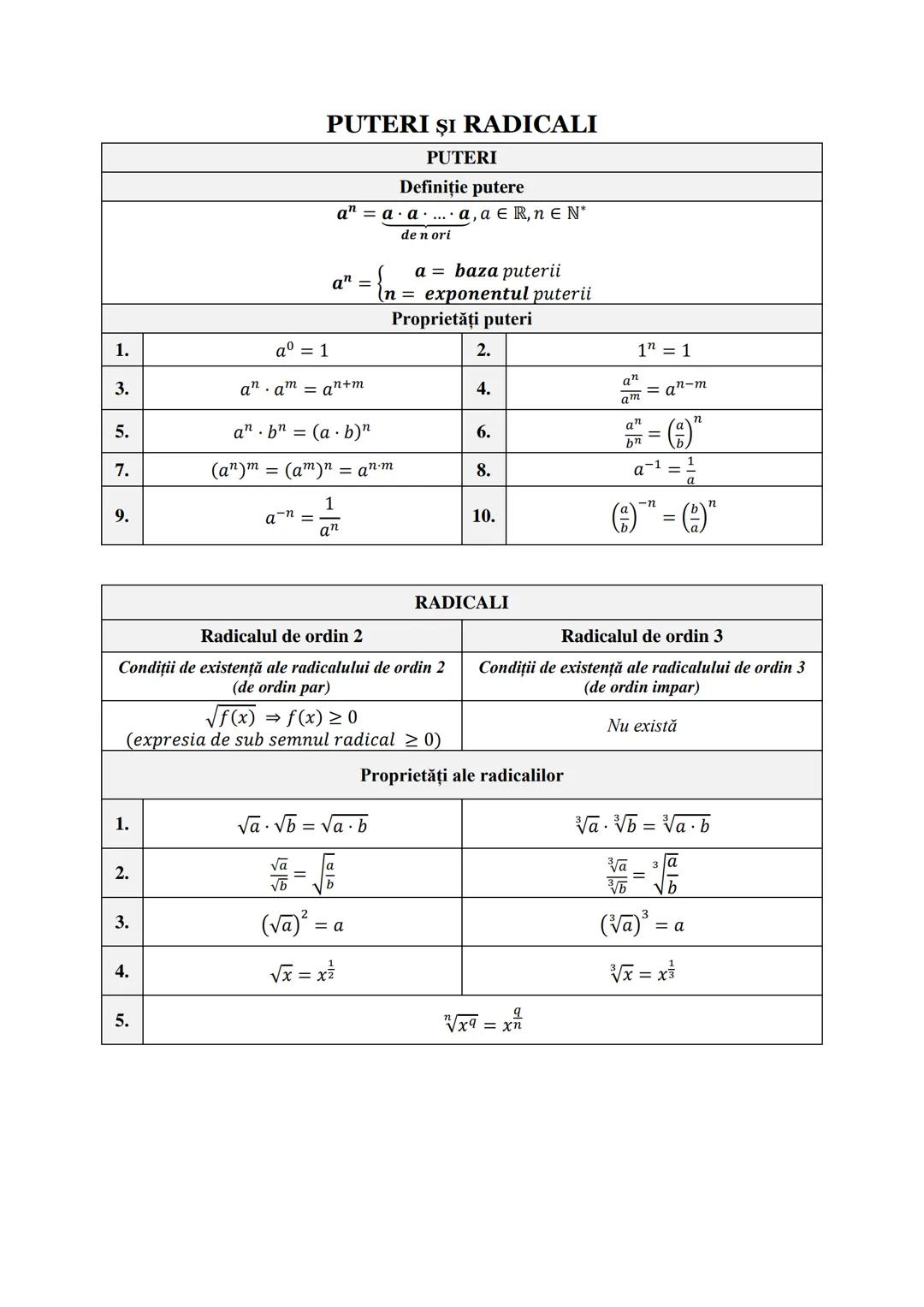
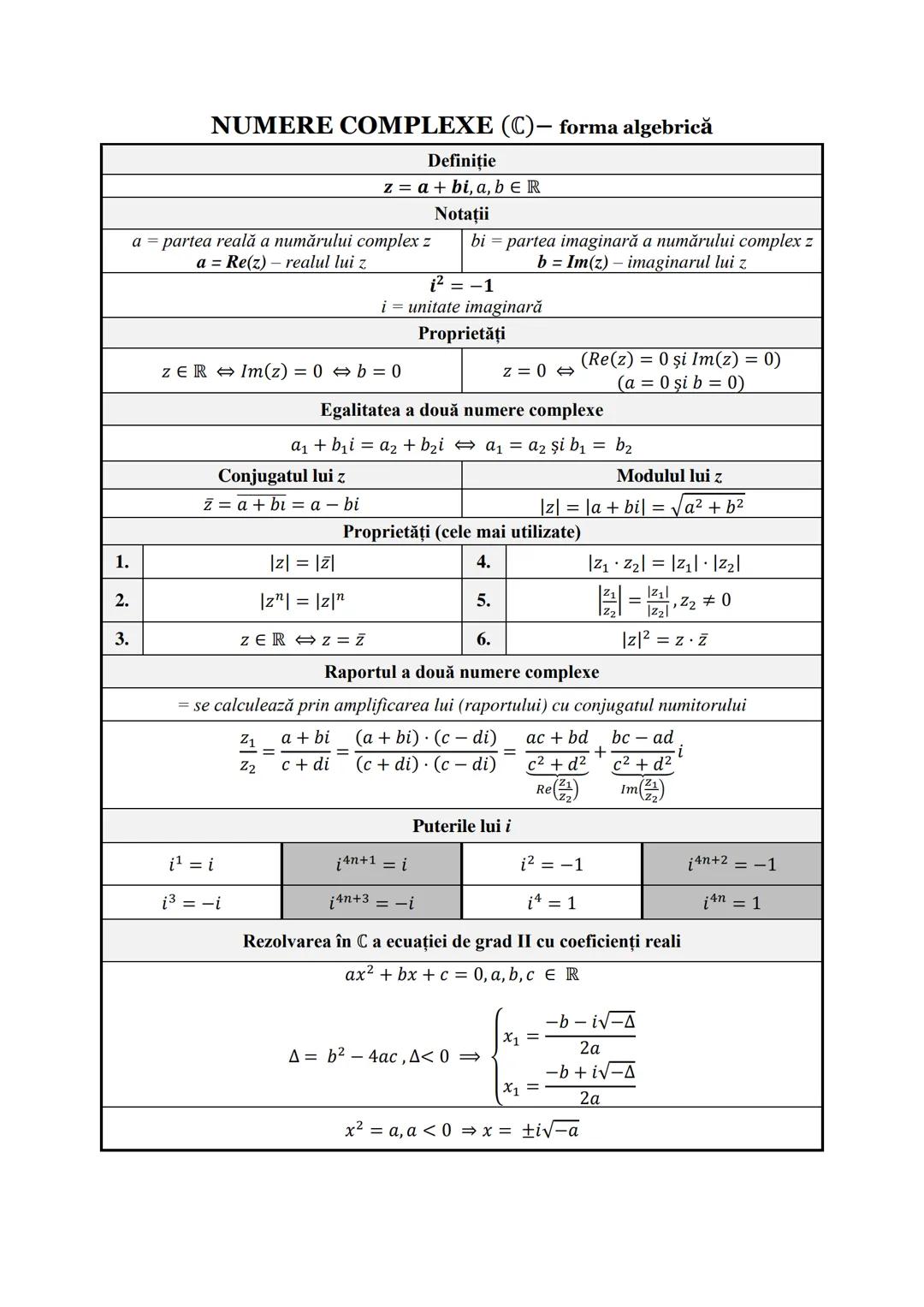
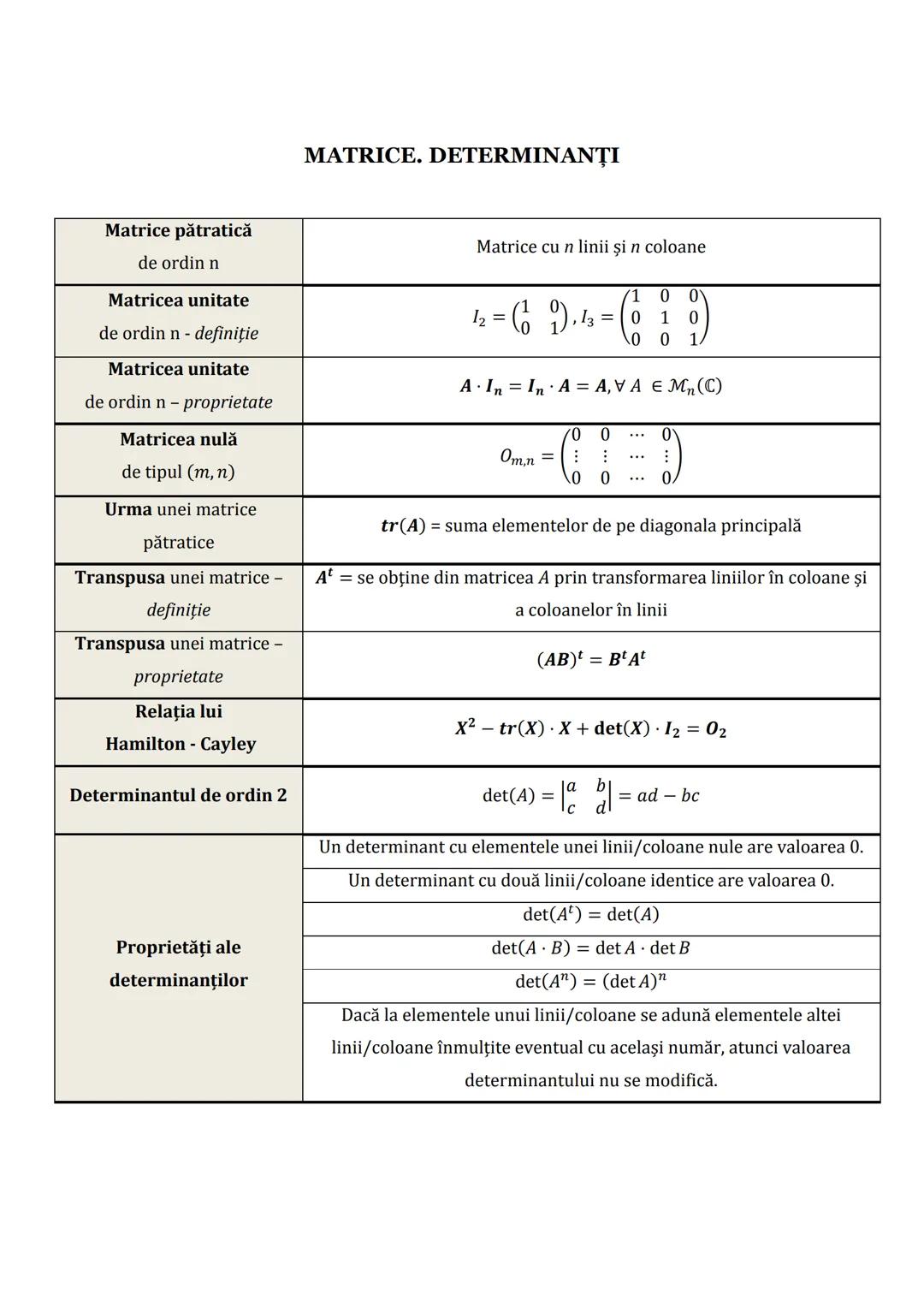
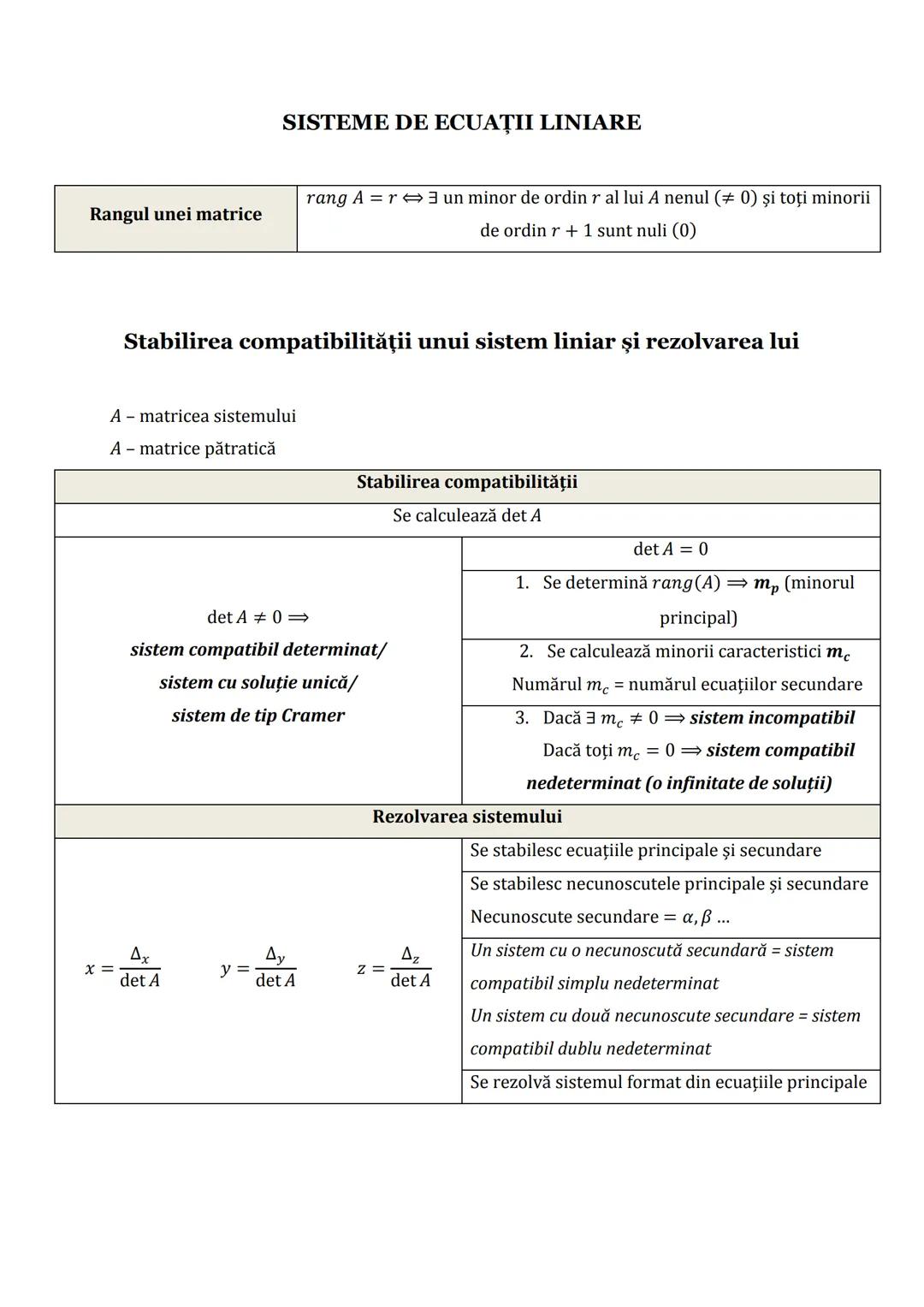
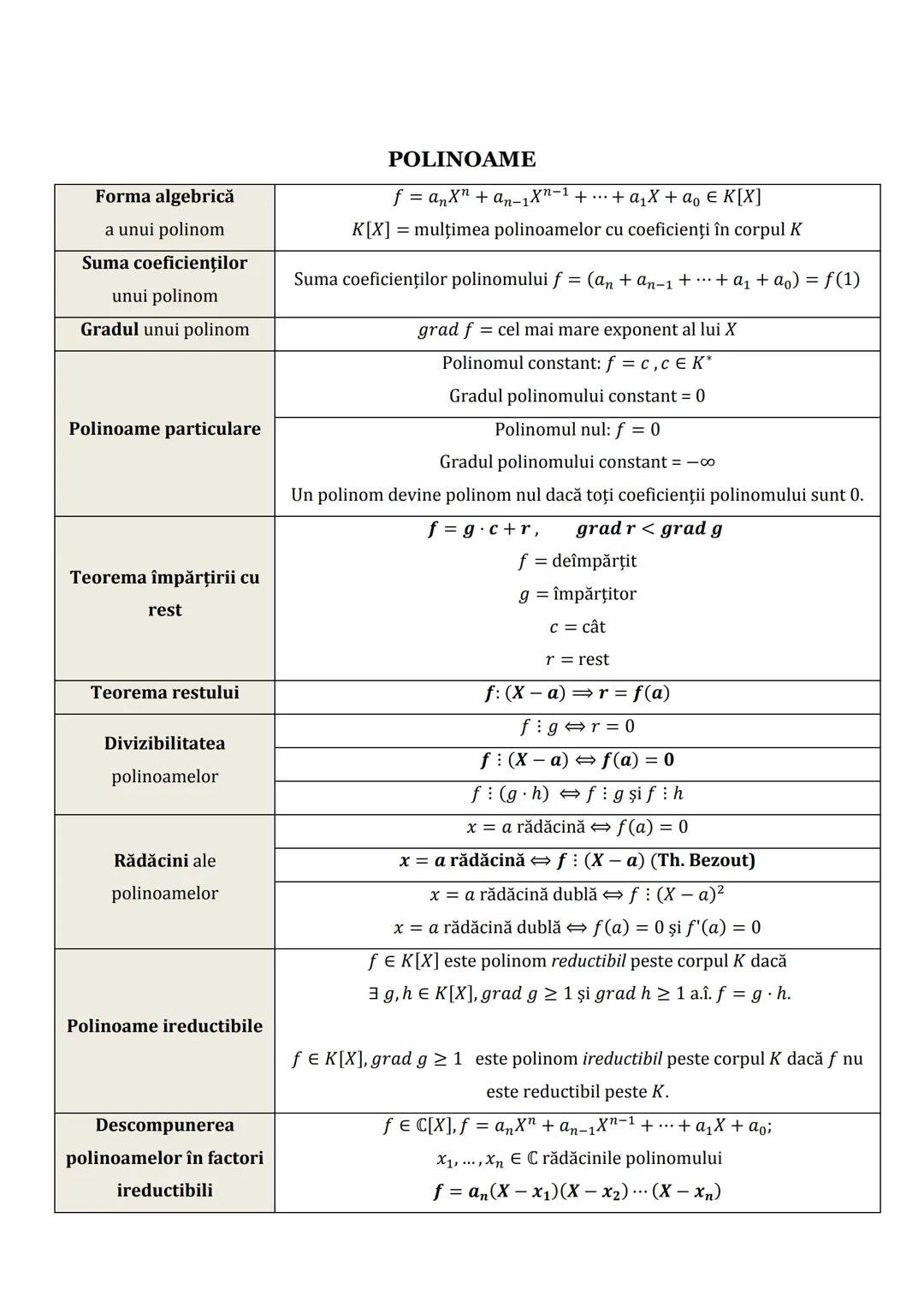
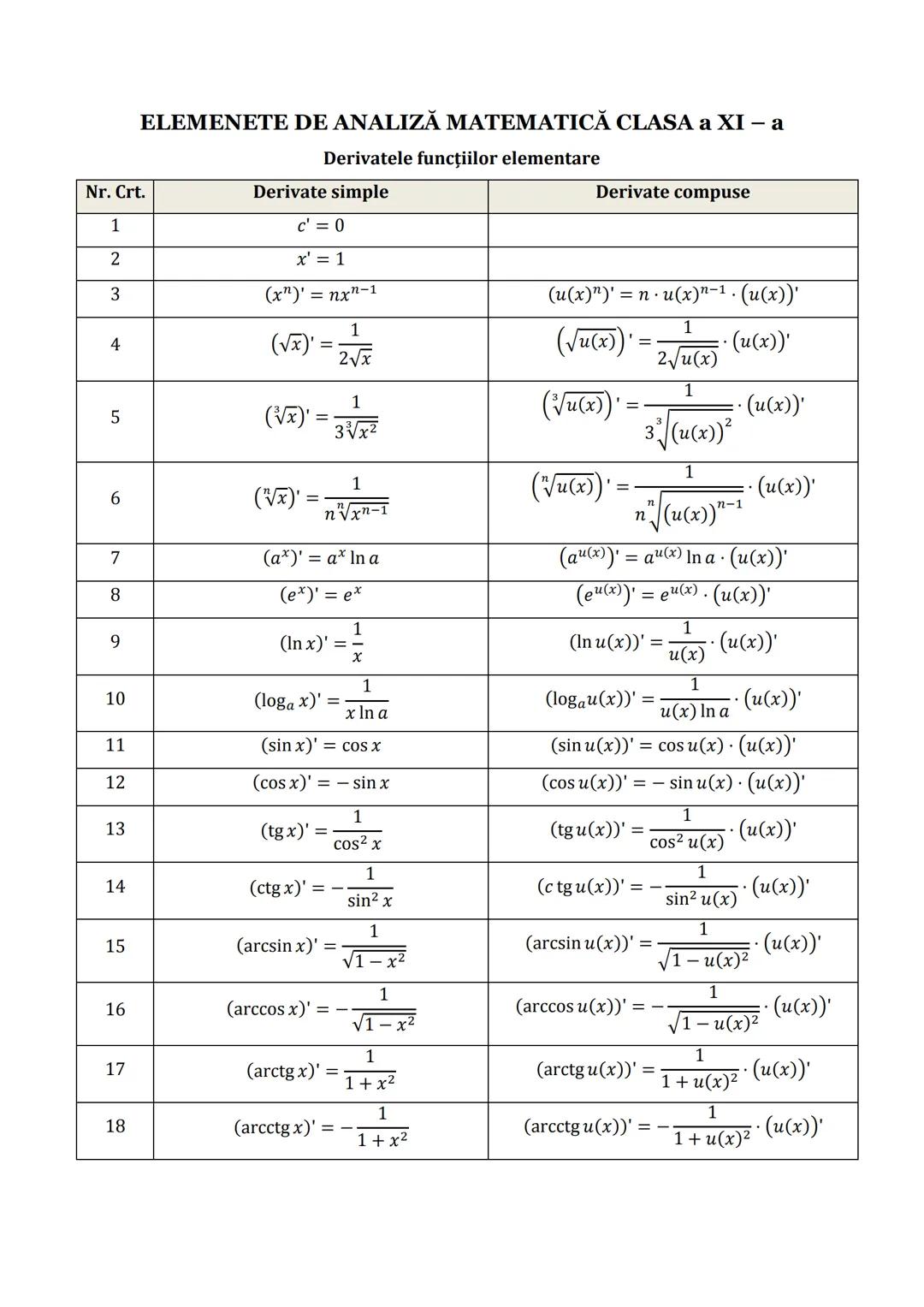
Formule de Calcul Prescurtat și Funcții Utile

Formulele de calcul prescurtat sunt instrumente puternice care te ajută să rezolvi rapid diverse expresii. Sunt esențiale pentru algebră și analiză matematică.

Diferența de pătrate: $a^2 - b^2 = (a-b)(a+b)$ - foarte utilă pentru factorizări.

Pătratul unei sume/diferențe:

• $(a+b)^2 = a^2 + 2ab + b^2$
• $(a-b)^2 = a^2 - 2ab + b^2$

Pentru expresii de gradul trei, reține:

• $a^3 - b^3 = (a-b)(a^2 + ab + b^2)$
• $a^3 + b^3 = (a+b)(a^2 - ab + b^2)$

💡 Observație importantă: Când lucrezi cu diferențe de cuburi, semnul din mijlocul parantezei a doua $a^2 + ab + b^2$ este mereu PLUS, iar pentru sume de cuburi, semnul este MINUS.

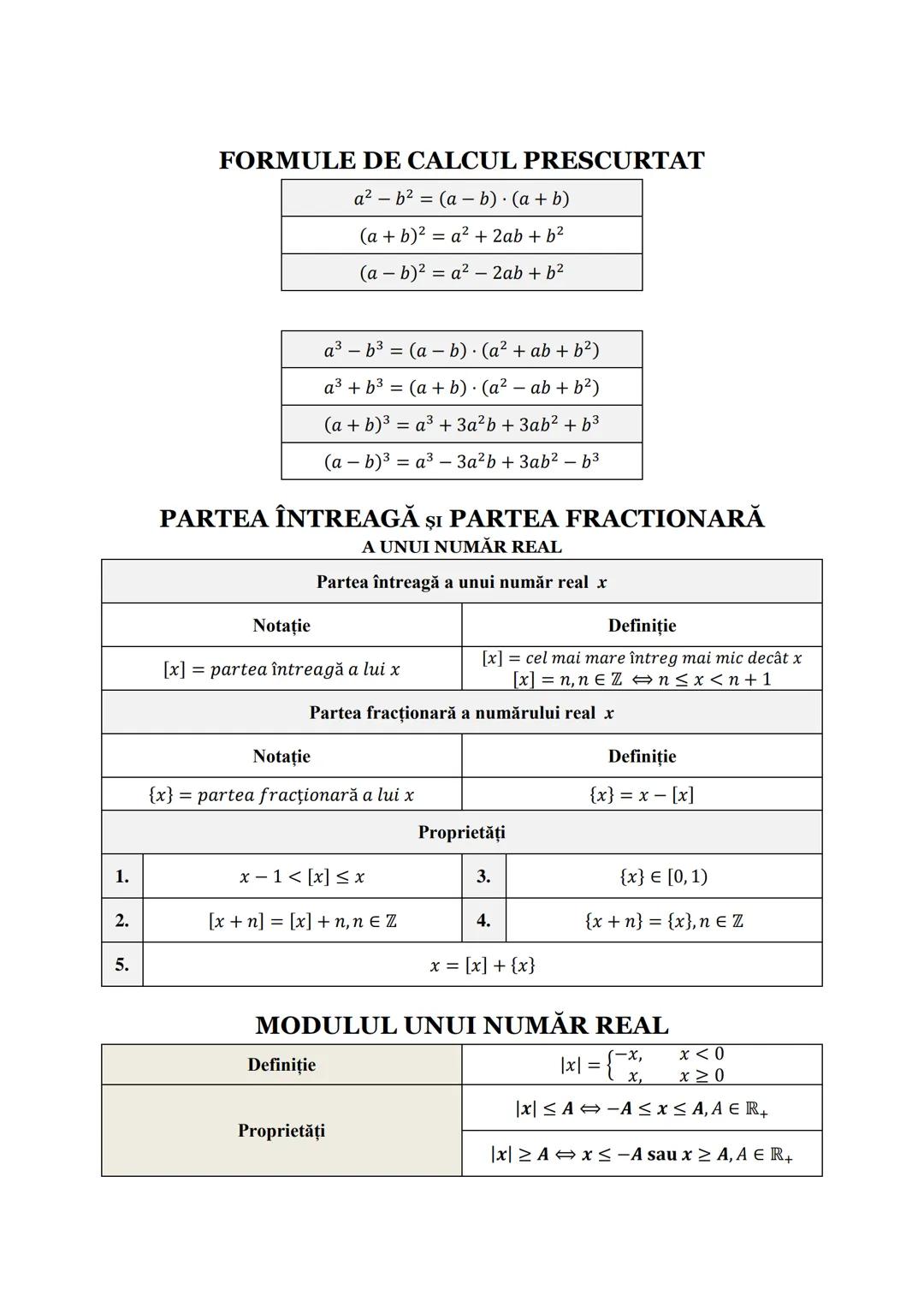
Partea întreagă $x$ a unui număr real x reprezintă cel mai mare număr întreg mai mic sau egal cu x. De exemplu, $3.7$ = 3, $-1.2$ = -2.

Partea fracționară {x} = x - $x$ și este mereu între 0 și 1: ${x} \in [0,1)$.

Modulul unui număr real este definit ca $|x| = \begin{cases} x, x \geq 0 \ -x, x < 0 \end{cases}$ și reprezintă distanța de la x la 0 pe axa numerelor.

Funcții - Definiții și Proprietăți Fundamentale

Funcțiile sunt relații matematice ce asociază fiecărui element dintr-o mulțime un singur element dintr-o altă mulțime. Le întâlnești în multe situații practice.

O funcție f se notează f: A → B, x → f(x), unde:

• A = domeniul funcției (valori de intrare)
• B = codomeniul funcției (unde pot exista valorile de ieșire)
• f(x) = regula care transformă x în f(x)

Graficul unei funcții (Gf) este mulțimea punctelor (x, f(x)) din plan. Punctul (x, y) aparține graficului dacă și numai dacă f(x) = y.

Pentru a găsi punctele de intersecție cu axa Ox, rezolvă ecuația f(x) = 0. Pentru a găsi punctul de intersecție cu axa Oy, calculează f(0).

💡 Sfat practic: Când trebuie să găsești intersecția graficelor a două funcții, rezolvă ecuația f(x) = g(x) pentru a afla absicisa (x), apoi calculează ordonata (y) folosind oricare dintre funcții.

Compunerea funcțiilor este o operație prin care aplicăm o funcție rezultatului altei funcții: (f∘g)(x) = f(g(x)). Ține minte că ordinea contează!

Tipuri și Proprietăți ale Funcțiilor

O funcție f este pară dacă f$-x$ = f(x) pentru orice x din domeniu. Graficul unei funcții pare este simetric față de axa Oy.

O funcție f este impară dacă f$-x$ = -f(x) pentru orice x din domeniu. Graficul unei funcții impare este simetric față de origine.

Funcțiile periodice au proprietatea că f$x+T$ = f(x) pentru orice x din domeniu. T este perioada funcției, iar cea mai mică perioadă nenulă pozitivă se numește perioadă principală.

Imaginea unei funcții f:A→B este mulțimea valorilor pe care le ia funcția: Im f = {f(x) | x ∈ A}.

💡 Reține: O funcție poate fi injectivă, surjectivă, sau bijectivă. Aceste proprietăți sunt esențiale pentru a determina dacă o funcție are inversă.

O funcție este injectivă dacă valori diferite din domeniu produc valori diferite în codomeniu: x₁ ≠ x₂ ⇒ f(x₁) ≠ f(x₂).

O funcție este surjectivă dacă orice element din codomeniu este imaginea cel puțin a unui element din domeniu.

O funcție este bijectivă dacă este atât injectivă, cât și surjectivă. Doar funcțiile bijective au funcție inversă, notată f⁻¹.

Funcțiile monotone păstrează sau inversează relațiile de ordine. O funcție este crescătoare dacă x₁ < x₂ ⇒ f(x₁) ≤ f(x₂) și strict crescătoare dacă x₁ < x₂ ⇒ f(x₁) < f(x₂).

Funcția de Gradul I

Funcția de gradul I, cunoscută și ca funcție liniară, este una dintre cele mai simple și mai utilizate funcții în matematică.

Forma generală a funcției de gradul I este f(x) = ax + b, unde a, b ∈ ℝ și a ≠ 0. Graficul acestei funcții este o dreaptă în plan.

Monotonia funcției depinde de valoarea lui a:

• Dacă a > 0, funcția este strict crescătoare (crește de la stânga la dreapta)
• Dacă a < 0, funcția este strict descrescătoare (scade de la stânga la dreapta)

Pentru a determina semnul funcției, rezolvă ecuația f(x) = 0, care dă x = -b/a. Această valoare împarte domeniul în două zone:

• Pentru x < -b/a, funcția are semn contrar lui a
• Pentru x > -b/a, funcția are același semn ca a

💡 Aplicație practică: Funcțiile de gradul I apar în multe situații din viața reală, cum ar fi costurile liniare $cost fix + cost variabil per unitate$, mișcarea uniformă, sau relații liniare între două mărimi.

Rețineți că panta dreptei (a) reprezintă rata de schimbare a funcției - cu cât valoarea absolută a lui a este mai mare, cu atât dreapta este mai înclinată.

Funcția de Gradul II

Funcția de gradul II, f(x) = ax² + bx + c (a ≠ 0), are graficul o parabolă care poate fi orientată în sus (a > 0) sau în jos (a < 0).

Punctul cel mai important al parabolei este vârful V, cu coordonatele:

• x = -b/(2a) (abscisa vârfului)
• y = -Δ/(4a) (ordonata vârfului), unde Δ = b² - 4ac

Când a < 0, vârful este punct de maxim și valoarea maximă a funcției este f₍ₘₐₓ₎ = -Δ/(4a). Când a > 0, vârful este punct de minim și valoarea minimă a funcției este f₍ₘᵢₙ₎ = -Δ/(4a).

💡 Pont important: Axa de simetrie a parabolei are ecuația x = -b/(2a) și trece prin vârful parabolei.

Poziția parabolei față de axa Ox depinde de discriminantul Δ = b² - 4ac:

• Dacă Δ > 0: parabola intersectează axa Ox în două puncte distincte
• Dacă Δ = 0: parabola este tangentă axei Ox $atinge axa Ox într-un singur punct$
• Dacă Δ < 0: parabola nu intersectează axa Ox

Imaginea funcției depinde de orientarea parabolei:

• Dacă a < 0: Im f = (-∞, -Δ/(4a)]
• Dacă a > 0: Im f = [-Δ/(4a), +∞)

Ecuații Iraționale și Transcendente

Ecuațiile iraționale conțin necunoscuta sub radical. Sunt importante pentru modelarea multor fenomene din fizică și inginerie.

Pentru ecuația $\sqrt{f(x)} = g(x)$, trebuie să impui condiții de existență: $f(x) \geq 0$ și $g(x) \geq 0$. Apoi ridici ambele părți la pătrat: $f(x) = g(x)²$. Pentru radicali de ordin impar ca $\sqrt[3]{f(x)} = g(x)$ nu ai condiții pentru f(x).

Atenție! După rezolvarea ecuației, verifică întotdeauna soluțiile în ecuația inițială, deoarece ridicarea la putere poate introduce soluții false.

Ecuațiile exponențiale au forma $a^{f(x)} = a^{g(x)}$ sau $a^{f(x)} = b$. Pentru primul tip, obții $f(x) = g(x)$ (când a > 0, a ≠ 1). Pentru al doilea tip, aplică logaritm: $f(x) = \log_a b$.

💡 Strategie utilă: Pentru ecuații de forma $a^{f(x)} = b^{g(x)}$, aplică logaritm natural: $f(x) \ln a = g(x) \ln b$.

Ecuațiile logaritmice conțin necunoscuta în argument de logaritm. Pentru $\log_a f(x) = \log_a g(x)$, obții $f(x) = g(x)$ (cu condiția că $f(x) > 0$ și $g(x) > 0$). Pentru $\log_a f(x) = N$, obții $f(x) = a^N$.

Ecuații Trigonometrice

Ecuațiile trigonometrice sunt esențiale în fizică, inginerie și multe alte domenii. Ele modelează fenomene periodice precum undele sau oscilațiile.

Ecuațiile fundamentale și soluțiile lor generale sunt:

• sin x = a $a ∈ [-1, 1]$: x = (-1)ᵏ · arcsin a + kπ, k ∈ ℤ
• cos x = a $a ∈ [-1, 1]$: x = ± arccos a + 2kπ, k ∈ ℤ
• tg x = a (a ∈ ℝ): x = arctg a + kπ, k ∈ ℤ
• ctg x = a (a ∈ ℝ): x = arcctg a + kπ, k ∈ ℤ

Pentru ecuații de forma sin f(x) = sin g(x), obții: f(x) = (-1)ᵏ · g(x) + kπ, k ∈ ℤ. Pentru cos f(x) = cos g(x), obții: f(x) = ±g(x) + 2kπ, k ∈ ℤ.

💡 Atenție importantă: Când folosești substituția tg$x/2$ = t pentru a rezolva ecuații de forma a·cos x + b·sin x + c = 0, verifică și valorile x = $2k+1$π, k ∈ ℤ care pot fi soluții pierdute în proces.

Formulele fundamentale precum sin²x + cos²x = 1 și cos 2x = 2cos²x - 1 = 1 - 2sin²x sunt deosebit de utile în rezolvarea ecuațiilor trigonometrice mai complexe.

Geometrie Analitică în Plan

Geometria analitică combină algebra cu geometria, permițând rezolvarea problemelor geometrice prin calcule algebrice.

Poziții relative a două drepte:

• Două drepte sunt paralele dacă și numai dacă au aceeași pantă: d₁ ∥ d₂ ⇔ m₍ₐ₁₎ = m₍ₐ₂₎
• Două drepte sunt perpendiculare dacă și numai dacă produsul pantelor lor este -1: d₁ ⊥ d₂ ⇔ m₍ₐ₁₎ · m₍ₐ₂₎ = -1

Pentru dreptele d₁: a₁x + b₁y + c₁ = 0 și d₂: a₂x + b₂y + c₂ = 0:

• Dreptele sunt concurente (se intersectează) dacă a₁/a₂ ≠ b₁/b₂
• Dreptele sunt paralele dacă a₁/a₂ = b₁/b₂ ≠ c₁/c₂
• Dreptele coincid dacă a₁/a₂ = b₁/b₂ = c₁/c₂

💡 Aplicație practică: Pentru a calcula aria unui triunghi cunoscând coordonatele vârfurilor A, B și C, folosește determinantul: A₍ₜᵣᵢₐₙₙₑ₎ = (1/2)|Δ|, unde Δ este determinantul matricei formate din coordonatele punctelor și coloana de 1.

Coliniaritatea a trei puncte se verifică prin calcularea determinantului format din coordonatele lor: A, B, C sunt coliniare ⇔ Δ = 0.

Distanța de la un punct la o dreaptă se calculează cu formula: d(A, d) = |ax₍ₐ₎ + by₍ₐ₎ + c|/√$a² + b²$.

Centrul de greutate al unui triunghi ABC are coordonatele: x₍ᵍ₎ = $x₍ₐ₎ + x₍ᵦ₎ + x₍ᴄ₎$/3 și y₍ᵍ₎ = $y₍ₐ₎ + y₍ᵦ₎ + y₍ᴄ₎$/3.