Determinarea inversei unei matrice pătratice

Pentru a calcula inversa unei matrice pătratice de ordin 2 sau 3 urmăm patru pași esențiali:

1. Calculăm determinantul matricei. Dacă determinantul este diferit de zero, atunci matricea este inversabilă $adică există A^-1$.

2. Găsim transpusa matricei, schimbând liniile cu coloanele.

3. Determinăm matricea adjunctă A*, înlocuind fiecare element din transpusă cu complementul său algebric.

💡 Operațiile de inversare a matricelor par complicate la început, dar cu puțină practică vei observa că pașii urmează o logică clară și repetabilă.

Complementul algebric și matricea adjunctă

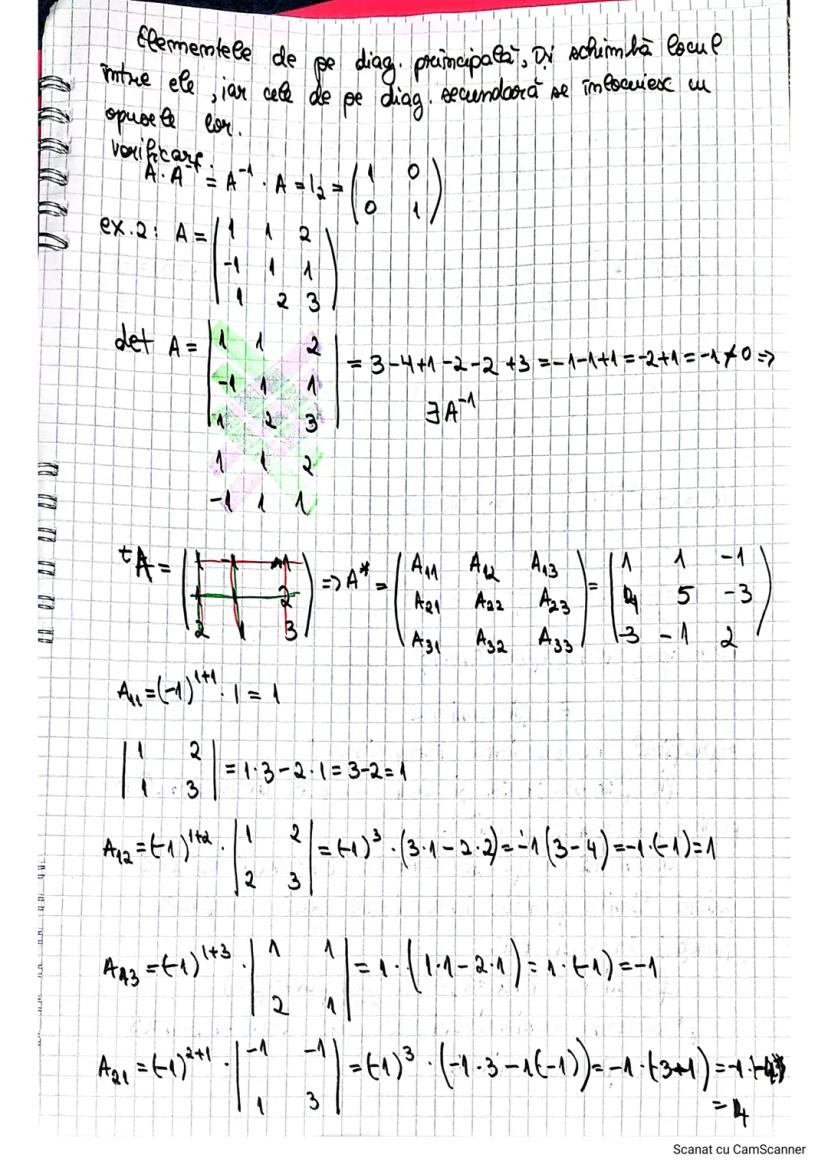
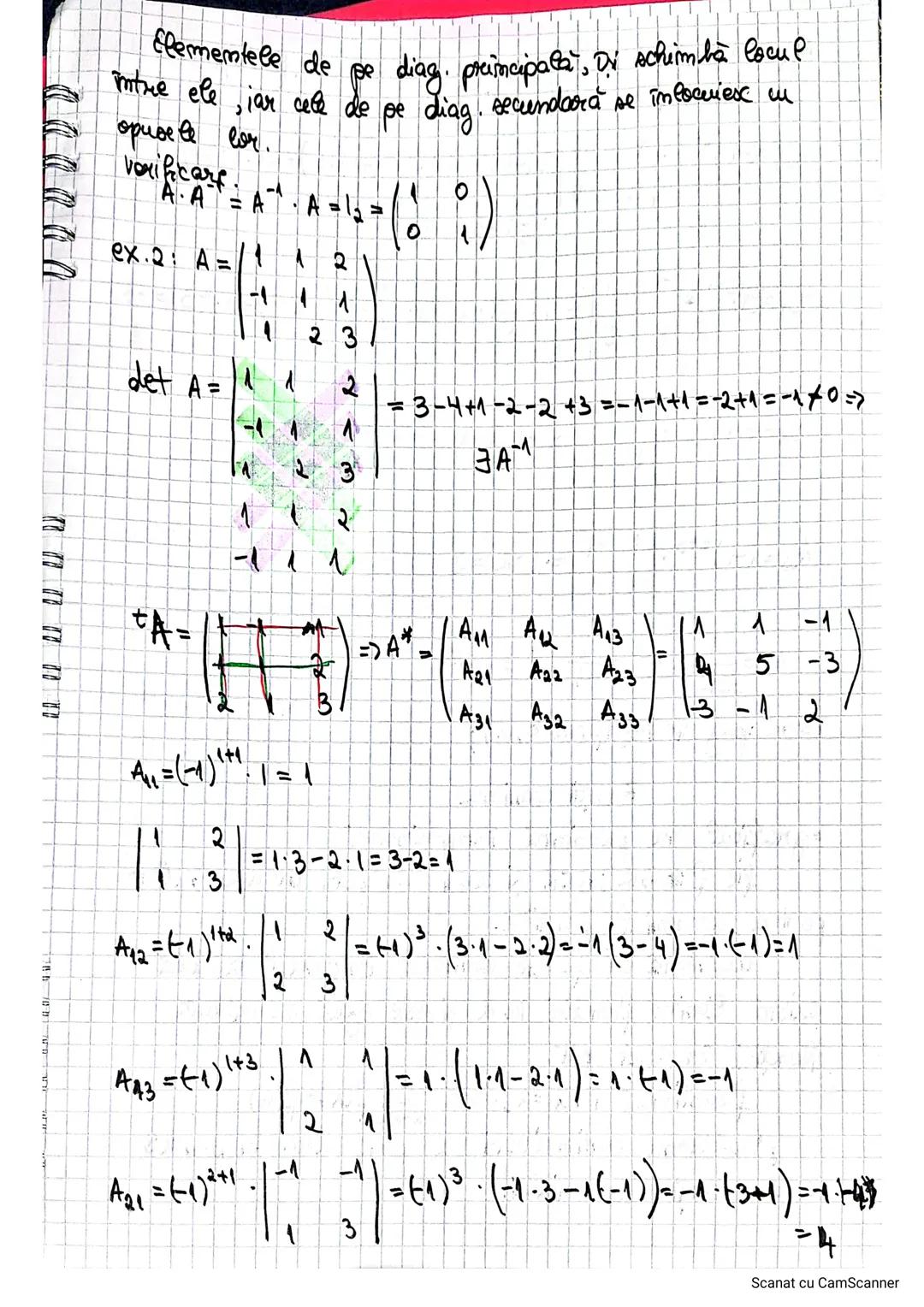
Complementul algebric al unui element a_ij, notat cu A_ij, se calculează astfel: A_ij = (-1)^$i+j$ · d_ij

Unde d_ij este minorul elementului a_ij, adică determinantul obținut prin eliminarea liniei i și a coloanei j.

Pasul final pentru a obține inversa este: A^(-1) = $1/det A$ · A*

Pentru matricele de ordin 2, putem determina adjuncta direct, fără a calcula transpusa: A = [a b; c d] => A* = $d -b; -c a$

💡 Observă modelul pentru matricele de ordin 2: elementele de pe diagonala principală își păstrează poziția, iar cele de pe diagonala secundară își schimbă semnul.

Verificarea și exemplul pentru matrice de ordin 3

La matricele de ordin 2, elementele de pe diagonala principală își schimbă locul între ele, iar cele de pe diagonala secundară devin opusele lor.

Pentru a verifica corectitudinea inversei, înmulțim matricea originală cu inversa sa și trebuie să obținem matricea identitate: A · A^(-1) = I.

Calculul inversei pentru o matrice de ordin 3 urmează aceiași pași, dar implică mai multe calcule pentru determinanți și complemente algebrice:

1. Calculăm determinantul matricei
2. Găsim transpusa
3. Calculăm complementele algebrice pentru fiecare element
4. Formăm matricea adjunctă
5. Împărțim adjuncta la determinant

💡 Când lucrezi cu matrice de ordin 3, organizează-ți calculele cu atenție pentru a evita erorile. Verifică întotdeauna rezultatul final prin înmulțirea A · A^(-1).