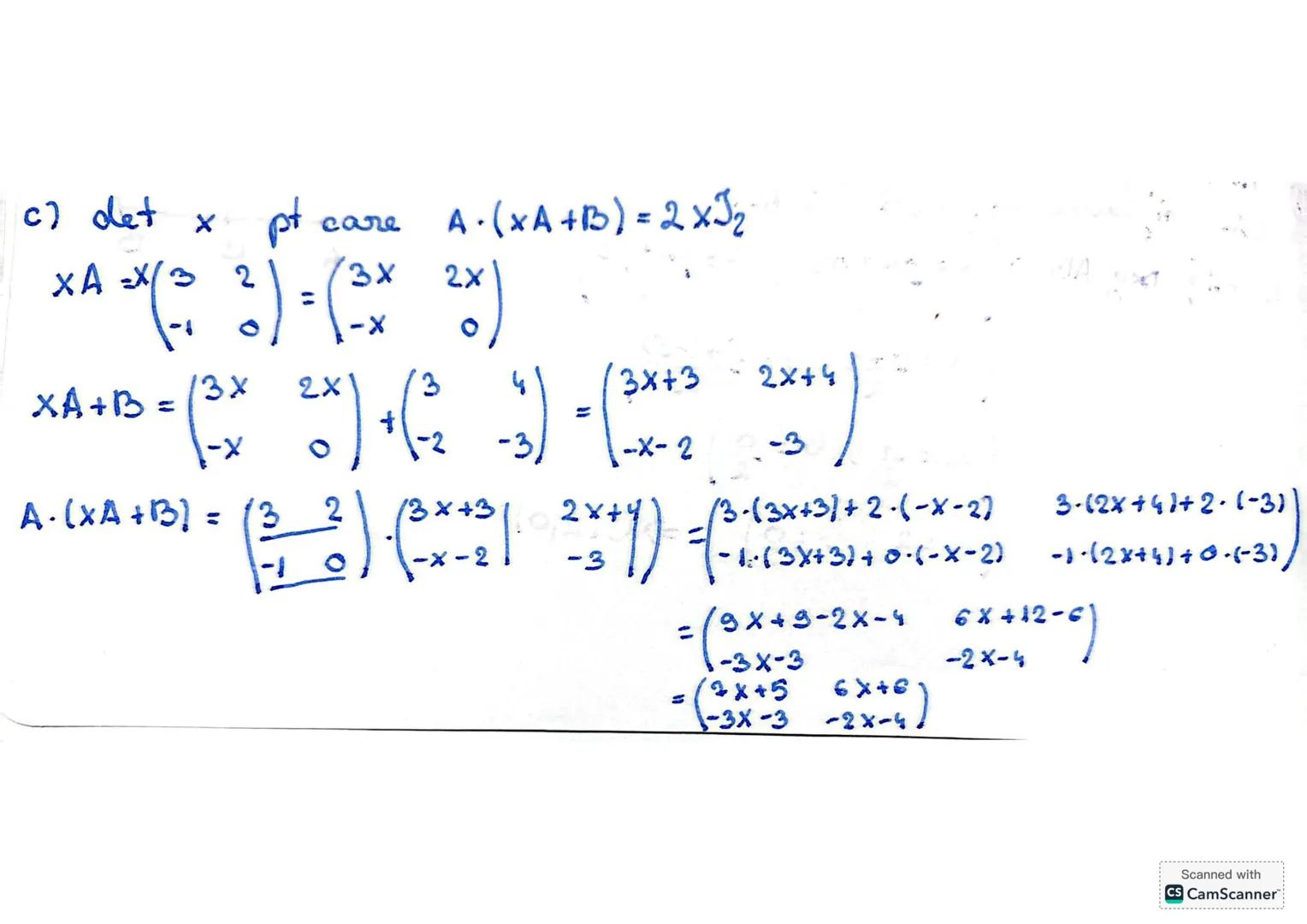Structura subiectului de bacalaureat - Matematică M_tehnologic

Testul de bacalaureat la matematică M_tehnologic este structurat în trei subiecte principale, având în total 30 de puncte fiecare. Se acordă 10 puncte din oficiu, iar timpul de lucru este de trei ore.

Primul subiect conține șase exerciții diverse, de la operații cu fracții și funcții până la probabilități și trigonometrie. Fiecare exercițiu valorează 5 puncte și testează concepte fundamentale.

Al doilea subiect se axează pe probleme de algebră liniară și legi de compoziție, împărțit în două părți: una cu matrici și determinanți, alta cu operații pe mulțimea numerelor reale.

Sfat util: Pentru rezolvarea exercițiilor din Subiectul I, nu este nevoie de calcule complicate - concentrează-te pe aplicarea corectă a formulelor și proprietăților de bază!

Subiectul al III-lea abordează analiza matematică, cu accent pe studiul funcțiilor și calculul integral. Acest subiect necesită deseori demonstrații și justificări mai detaliate ale pașilor de rezolvare.

Calculul determinantului matricei A

Calculul determinantului unei matrici este un element esențial pentru rezolvarea problemelor de algebră liniară. În cazul matricei A de ordinul 2, acesta se calculează folosind formula clasică.

Pentru a calcula determinantul matricei $A=\begin{pmatrix} 3 & 2 \ -1 & 0 \end{pmatrix}$, aplicăm formula:

$$\det A = \begin{vmatrix} 3 & 2 \ -1 & 0 \end{vmatrix} = 3 \cdot 0 - 2 \cdot (-1)$$

Efectuând operațiile, obținem: $$\det A = 0 - (-2) = 0 + 2 = 2$$

Atenție: Pentru calculul determinanților de ordin 2, folosește întotdeauna produsul elementelor de pe diagonala principală minus produsul elementelor de pe diagonala secundară!

Acest rezultat, $\det A = 2$, va fi util în următoarele probleme legate de matricea A, în special pentru calculul inversei sau rezolvarea sistemelor de ecuații.

Verificarea relației între matrici

Relațiile între matrici sunt frecvent întâlnite la examenul de bacalaureat. În acest caz, trebuie să demonstrăm că $B+3I_2=2A$.

Pentru a verifica această relație, calculăm separat fiecare parte:

Pasul 1: Calculăm $3I_2$ $$3I_2 = 3 \begin{pmatrix} 1 & 0 \ 0 & 1 \end{pmatrix} = \begin{pmatrix} 3 & 0 \ 0 & 3 \end{pmatrix}$$

Pasul 2: Calculăm $B+3I_2$ $$B+3I_2 = \begin{pmatrix} 3 & 4 \ -2 & -3 \end{pmatrix} + \begin{pmatrix} 3 & 0 \ 0 & 3 \end{pmatrix} = \begin{pmatrix} 6 & 4 \ -2 & 0 \end{pmatrix}$$

Pasul 3: Calculăm $2A$ $$2A = 2 \begin{pmatrix} 3 & 2 \ -1 & 0 \end{pmatrix} = \begin{pmatrix} 6 & 4 \ -2 & 0 \end{pmatrix}$$

Pont important: La adunarea a două matrici, se adună elementele de pe poziții corespondente, iar la înmulțirea cu un scalar, se înmulțește fiecare element al matricei cu acel scalar.

Astfel, am demonstrat că $B+3I_2=2A$, deoarece rezultatele obținute sunt identice.

Determinarea parametrului x din ecuația matriceală

Rezolvarea ecuațiilor matriceale este o aplicație importantă a algebrei liniare. În această problemă, trebuie să determinăm numărul real x pentru care $A \cdot (xA+B) = 2xI_2$.

Pasul 1: Calculăm $xA+B$ $$xA+B = x\begin{pmatrix} 3 & 2 \ -1 & 0 \end{pmatrix} + \begin{pmatrix} 3 & 4 \ -2 & -3 \end{pmatrix} = \begin{pmatrix} 3x+3 & 2x+4 \ -x-2 & -3 \end{pmatrix}$$

Pasul 2: Calculăm produsul $A \cdot (xA+B)$ $$A \cdot $xA+B$ = \begin{pmatrix} 3 & 2 \ -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 3x+3 & 2x+4 \ -x-2 & -3 \end{pmatrix}$$

Efectuând înmulțirea matricelor, obținem: $$A \cdot $xA+B$ = \begin{pmatrix} 9x+9-2x-4 & 6x+12-6 \ -3x-3 & -2x-4 \end{pmatrix} = \begin{pmatrix} 7x+5 & 6x+6 \ -3x-3 & -2x-4 \end{pmatrix}$$

Important: Verifică-ți de două ori calculele la înmulțirea matricelor, deoarece este o sursă frecventă de erori!

Pasul 3: Calculăm $2xI_2$ $$2xI_2 = 2x \begin{pmatrix} 1 & 0 \ 0 & 1 \end{pmatrix} = \begin{pmatrix} 2x & 0 \ 0 & 2x \end{pmatrix}$$

Finalizarea calculului pentru parametrul x

Pentru a rezolva ecuația matriceală $A \cdot (xA+B) = 2xI_2$, trebuie să comparăm elementele corespondente din cele două matrici și să stabilim valoarea lui x.

Comparând matricele, obținem sistemul de ecuații: $$\begin{cases} 7x+5 = 2x \ -3x-3 = 0 \ 6x+6 = 0 \ -2x-4 = 2x \end{cases}$$

Din a doua ecuație avem: $$-3x-3 = 0 \Rightarrow -3x = 3 \Rightarrow x = -1$$

Verificăm dacă x = -1 satisface și celelalte ecuații:

Pentru prima ecuație: $$7(-1)+5 = 2(-1) \Rightarrow -7+5 = -2 \Rightarrow -2 = -2 \checkmark$$

Pentru a treia ecuație: $$6(-1)+6 = 0 \Rightarrow -6+6 = 0 \checkmark$$

Pentru a patra ecuație: $$-2(-1)-4 = 2(-1) \Rightarrow 2-4 = -2 \Rightarrow -2 = -2 \checkmark$$

Reține: Soluția unei ecuații matriceale trebuie să satisfacă simultan toate condițiile rezultate din egalitatea matricelor!

Astfel, soluția ecuației matriceale este x = -1, deoarece această valoare satisface toate ecuațiile sistemului.