Puncte și Drepte

Punctele și dreptele sunt elementele de bază ale geometriei. Punctele pot fi coliniare când se află pe aceeași dreaptă, sau distincte când nu sunt pe aceeași dreaptă.

Dreptele pot fi concurente $se intersectează într-un singur punct$, paralele (nu se intersectează niciodată) sau perpendiculare (formează un unghi de 90°). Când vorbim despre simetricul unui punct, înseamnă că două puncte A și B sunt simetrice față de un punct M dacă M este mijlocul segmentului AB.

Geometria se bazează pe câteva axiome fundamentale: prin orice două puncte distincte trece o singură dreaptă, prin trei puncte necoliniare trece un singur plan, și prin orice punct exterior unei drepte putem construi o singură dreaptă paralelă la cea inițială.

💡 Ține minte! Axiomele sunt adevăruri fundamentale pe care se construiește întreaga geometrie. Nu trebuie demonstrate, ci sunt acceptate ca fiind adevărate.

Plane și Intersecții

Când lucrezi cu planele, este important să știi că dacă două plane distincte au un punct comun, atunci ele se intersectează de-a lungul unei drepte. Această proprietate este cunoscută ca axioma intersecției.

Poți determina un plan în mai multe moduri:

• Folosind trei puncte necoliniare
• Folosind o dreaptă și un punct exterior ei
• Folosind două drepte concurente (care se intersectează)
• Folosind două drepte paralele

Aceste metode sunt esențiale când rezolvi probleme de geometrie în spațiu. Fiecare metodă are aplicații practice în diferite situații.

💡 Sfat util: Când desenezi figuri geometrice în spațiu, folosește linii punctate pentru părțile care nu sunt vizibile direct, ca să-ți fie mai ușor să vizualizezi.

Puncte, Drepte și Plane

În geometrie, punctul este o figură geometrică fără dimensiune, reprezentat prin urma lăsată de vârful unui creion. Nu are lungime, lățime sau înălțime - e doar o poziție în spațiu.

Dreapta este o figură geometrică determinată de cel puțin două puncte distincte. Conform axiomei dreptei, prin oricare două puncte distincte trece o singură dreaptă. De asemenea, printr-un punct exterior unei drepte poate trece o singură paralelă la dreapta dată.

Planul este determinat de cel puțin 3 puncte necoliniare. Poți determina un plan și prin două drepte paralele sau două drepte concurente. Conform axiomei spațiului, există întotdeauna 4 puncte necoplanare (care nu se află în același plan).

💡 Reține: Toate aceste elemente de bază sunt necesare pentru a înțelege figurile geometrice mai complexe și relațiile dintre ele.

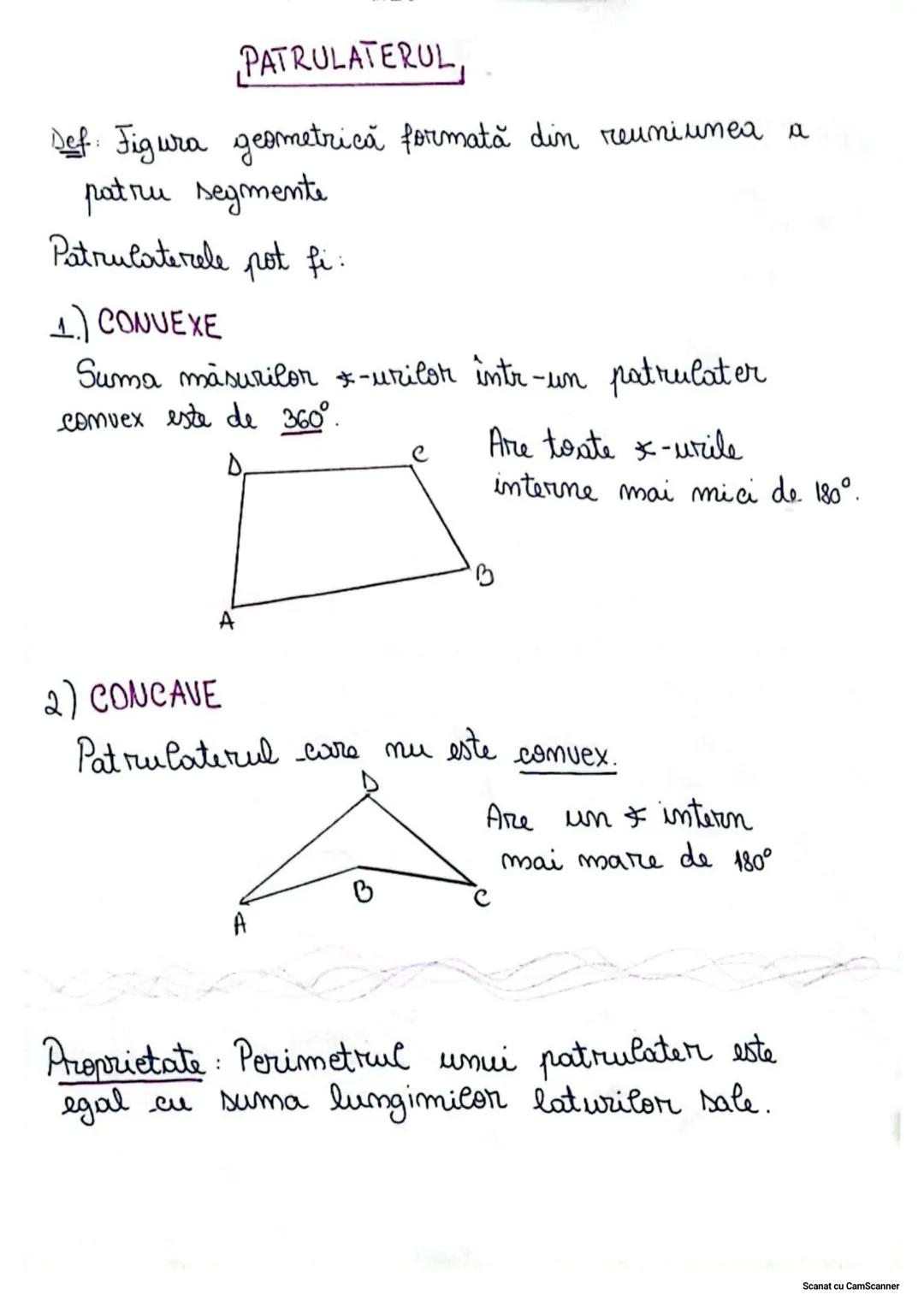
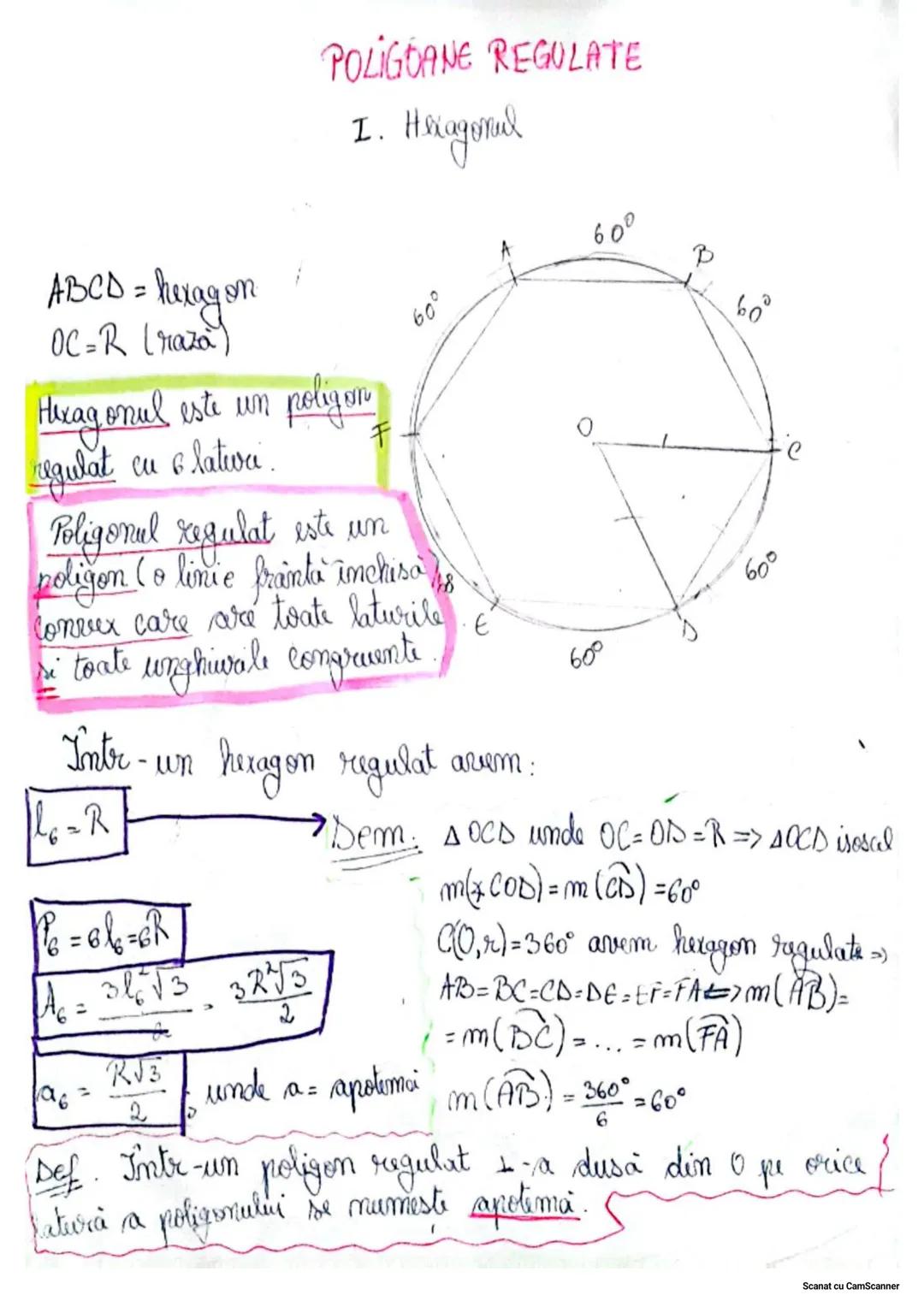
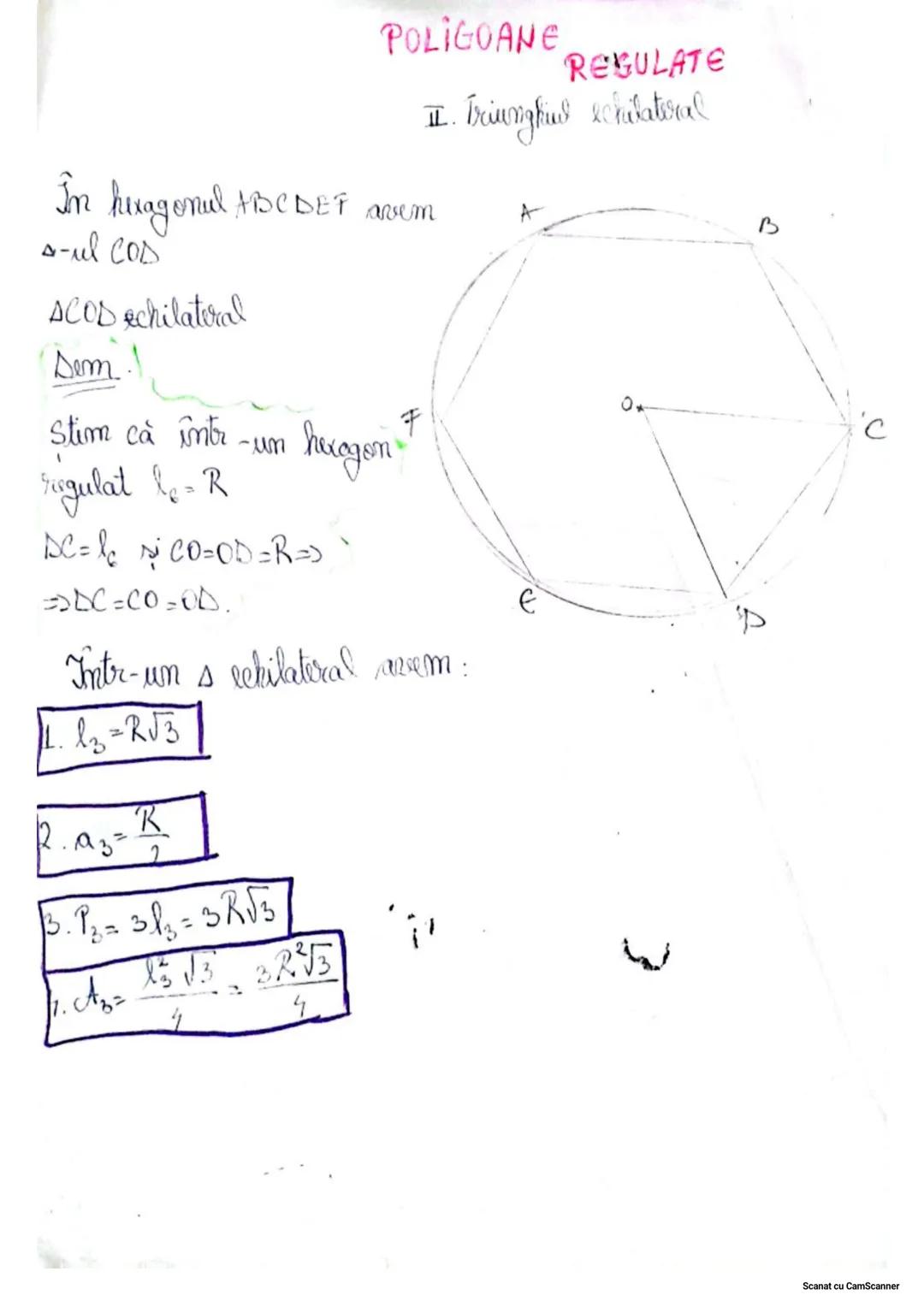
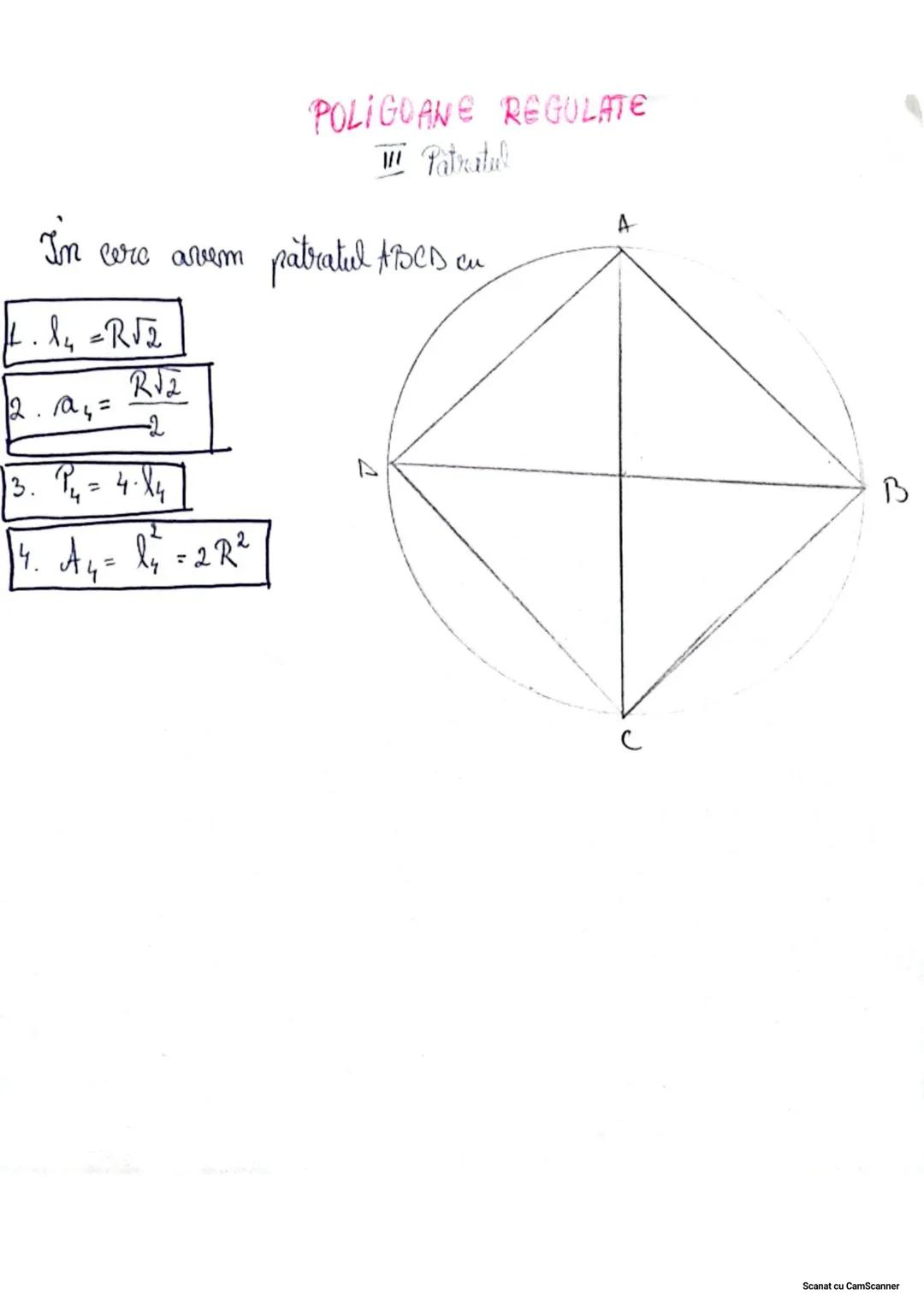
Proprietățile Triunghiurilor

Triunghiurile au proprietăți speciale în funcție de tipul lor. Triunghiul isoscel are două laturi congruente, unghiurile alăturate bazei sunt congruente, iar bisectoarea vârfului opus bazei este și înălțime și mediană.

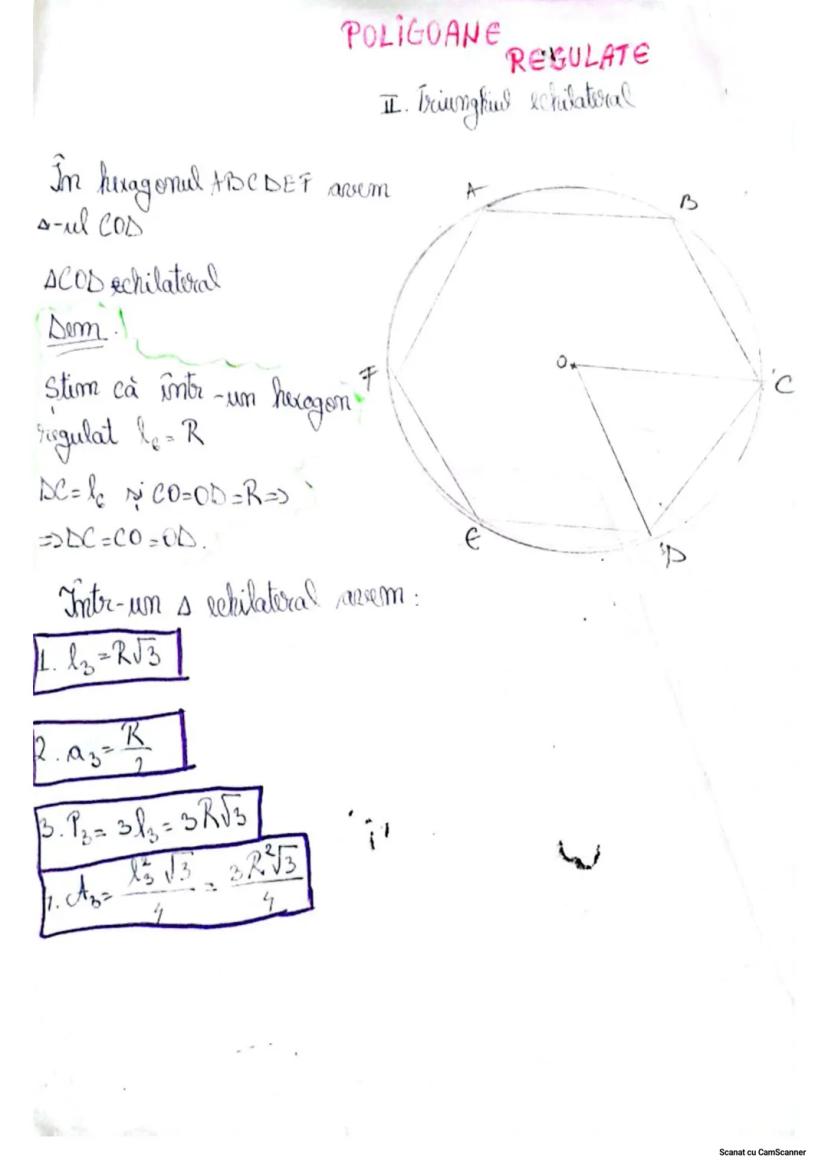
Triunghiul echilateral are toate cele trei laturi congruente și toate unghiurile de 60°. În acest triunghi, bisectoarea oricărui unghi este și mediană, înălțime și mediatoare.

Triunghiul dreptunghic are un unghi drept (90°) și două unghiuri ascuțite care sunt complementare (suma lor este 90°). În acest triunghi, mediana corespunzătoare ipotenuzei este jumătate din ipotenuză, iar cateta opusă unghiului de 30° este egală cu jumătate din ipotenuză.

💡 Important! Formula ariei unui triunghi este A = (baza × înălțimea)/2, dar pentru triunghiul echilateral poți folosi și formula A = (latura² × √3)/4.

Linii Importante în Triunghi

Înălțimea unui triunghi este segmentul perpendicular dus din vârf pe latura opusă. Cele trei înălțimi ale unui triunghi sunt concurente într-un punct numit ortocentru (H).

Mediana este segmentul care unește un vârf cu mijlocul laturii opuse. Cele trei mediane ale unui triunghi sunt concurente în centrul de greutate (G). Un lucru interesant este că centrul de greutate împarte fiecare mediană în raport de 2:1 începând de la vârf.

Aceste linii sunt esențiale pentru rezolvarea multor probleme de geometrie și pentru calcularea ariilor. Fiecare dintre ele are proprietăți specifice care te pot ajuta să găsești răspunsuri mai rapid.

💡 Trucul meu: Pentru a-ți aminti mai ușor, gândește-te că mediana "mediază" (leagă vârful de mijlocul laturii opuse), iar înălțimea este întotdeauna perpendiculară pe bază.

Mediatoare și Bisectoare

Mediatoarea unui segment este dreapta perpendiculară pe segment în mijlocul său. Proprietatea ei specială: orice punct de pe mediatoare se află la distanțe egale față de extremitățile segmentului. Cele trei mediatoare ale laturilor unui triunghi sunt concurente în punctul O, centrul cercului circumscris triunghiului.

Bisectoarea este semidreapta care pornește din vârful unui unghi și îl împarte în două unghiuri congruente. Într-un triunghi, cele trei bisectoare sunt concurente în punctul I, centrul cercului înscris. Acest punct se află la egală distanță față de toate laturile triunghiului.

Aceste linii sunt esențiale nu doar pentru geometrie, ci și pentru multe aplicații practice, de la arhitectură la design.

💡 Ajutor practic: Centrul cercului înscris este punctul din interiorul triunghiului care se află la egală distanță de toate cele trei laturi - este singurul punct din care poți desena un cerc care atinge toate laturile!

Relații Metrice în Triunghiul Dreptunghic

În triunghiurile dreptunghice există relații matematice foarte utile. Conform teoremei catetei, pătratul unei catete este egal cu produsul dintre ipotenuză și proiecția catetei pe ipotenuză: c² = ip × prip.

Teorema lui Pitagora este probabil cea mai cunoscută: suma pătratelor catetelor este egală cu pătratul ipotenuzei $c₁² + c₂² = ip²$. Această teoremă te ajută să calculezi orice latură a triunghiului dreptunghic când cunoști celelalte două.

Teorema înălțimii spune că pătratul înălțimii corespunzătoare ipotenuzei este egal cu produsul proiecțiilor catetelor pe ipotenuză: h² = pr₁ × pr₂. De asemenea, înălțimea se poate calcula folosind formula: h = (c₁ × c₂)/ip.

💡 Sfat util: Teorema lui Pitagora funcționează doar în triunghiuri dreptunghice, deci verifică întotdeauna că ai un unghi de 90° înainte de a o aplica!

Alte Teoreme Importante

Teorema Medianei ne spune că într-un triunghi dreptunghic, mediana care pornește din vârful unghiului drept are lungimea egală cu jumătate din ipotenuză: med = ip/2. Această teoremă te ajută să găsești rapid lungimea medianei când știi ipotenuza.

Teorema Unghiului de 30° afirmă că într-un triunghi dreptunghic, cateta opusă unghiului de 30° este egală cu jumătate din ipotenuză: c.op.∠30° = ip/2. Este foarte utilă în rezolvarea problemelor cu unghiuri speciale.

Teorema Bisectoarei spune că bisectoarea unui unghi al triunghiului împarte latura opusă în segmente proporționale cu laturile adiacente unghiului: BM/MC = AB/AC. Această teoremă te ajută să calculezi lungimile segmentelor când ai informații despre bisectoare.

💡 Observație: Teorema unghiului de 30° se aplică doar în triunghiuri dreptunghice care au un unghi de 30°, celălalt unghi ascuțit fiind de 60°.

Asemănarea Triunghiurilor

Teorema lui Thales este fundamentală în geometrie: dacă o dreaptă este paralelă cu o latură a unui triunghi și intersectează celelalte două laturi, atunci ea împarte aceste laturi în segmente proporționale: MN ∥ BC ⇒ AM/MB = AN/NC.

Două triunghiuri sunt asemenea când au unghiurile respective congruente și laturile proporționale. Notăm asemănarea așa: △ABC ∼ △MNP. Asta înseamnă că ∠A ≡ ∠M, ∠B ≡ ∠N, ∠C ≡ ∠P și raportul laturilor corespunzătoare este constant: AB/MN = AC/MP = BC/NP.

Conform teoremei fundamentale a asemănării, dacă △ADE ∼ △ABC, atunci unghiurile respective sunt congruente și laturile sunt proporționale. Această teoremă este foarte utilă pentru rezolvarea problemelor complexe de geometrie.

💡 Aplicație practică: Asemănarea triunghiurilor te ajută să măsori înălțimea obiectelor înalte precum copacii sau clădirile, folosind umbre sau alte metode indirecte!

Triunghiuri Asemenea

Triunghiurile asemenea au unghiurile respectiv congruente și laturile proporționale. Există trei cazuri de asemănare care te ajută să demonstrezi că două triunghiuri sunt asemenea:

1. U.U. $unghi-unghi$: când două perechi de unghiuri corespondente sunt congruente
2. L.U.L. $latură-unghi-latură$: când două perechi de laturi corespondente sunt proporționale și unghiurile dintre ele sunt congruente
3. L.L.L. $latură-latură-latură$: când toate cele trei perechi de laturi corespondente sunt proporționale

Un aspect important al triunghiurilor asemenea este raportul ariilor: dacă △ABC ∼ △MNP și raportul laturilor este k $AB/MN = k$, atunci raportul ariilor este k² $Aabc/Amnp = k²$, iar raportul perimetrelor este tot k.

💡 Aplicație: Asemănarea triunghiurilor este folosită în cartografie pentru a face hărți la scară și în artă pentru a redimensiona desenele proporțional.