Progresii - formule esențiale

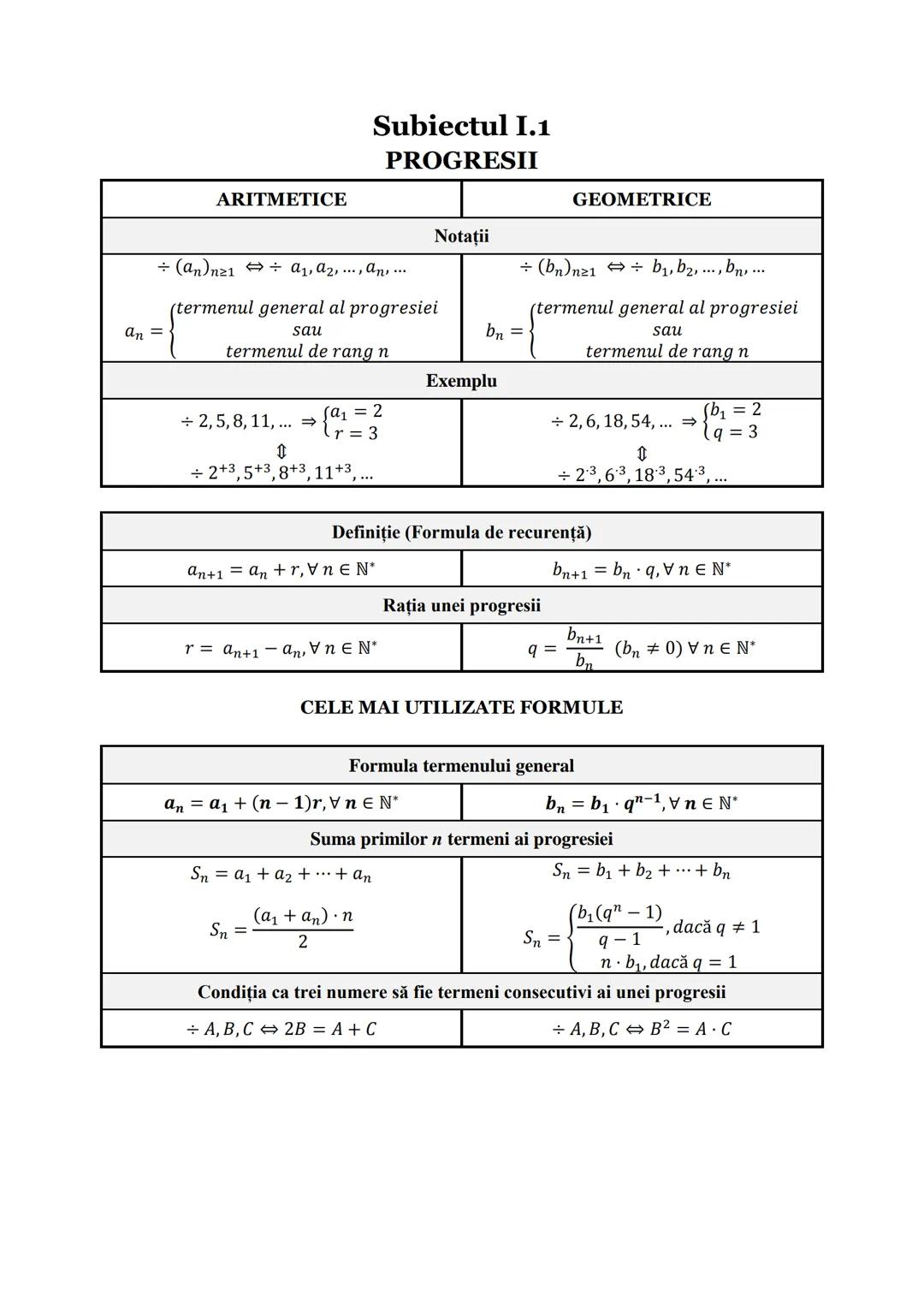
Progresiile sunt șiruri de numere care respectă anumite reguli. Există două tipuri principale: aritmetice și geometrice, fiecare cu proprietăți specifice.

În progresiile aritmetice, diferența dintre două numere consecutive este constantă. Notăm această diferență cu r (rația progresiei). De exemplu, în șirul 2, 5, 8, 11, ..., rația este 3. Formula termenului general este a_n = a_1 + $n - 1$r, unde a_1 este primul termen.

În progresiile geometrice, raportul dintre două numere consecutive este constant. Notăm acest raport cu q (rația progresiei). De exemplu, în șirul 2, 6, 18, 54, ..., rația este 3. Formula termenului general este b_n = b_1 · q^$n-1$, unde b_1 este primul termen.

💡 Pentru a verifica rapid dacă trei numere A, B, C sunt termeni consecutivi: într-o progresie aritmetică trebuie să avem 2B = A + C, iar într-o progresie geometrică trebuie să avem B² = A · C.

Suma primilor n termeni ai unei progresii aritmetice se calculează folosind formula: S_n = $a_1 + a_n$ · n / 2. Pentru progresii geometrice, formula este: S_n = b_1$q^n - 1$/$q - 1$ pentru q ≠ 1 și S_n = n · b_1 pentru q = 1.

Logaritmi - proprietăți și formule

Logaritmii sunt operații inverse exponențierii și sunt definiți astfel: dacă a^x = N, atunci x = log_a N. Pentru a exista logaritmul, trebuie respectate condițiile: a > 0, a ≠ 1 și N > 0.

Două tipuri importante de logaritmi sunt logaritmul zecimal (lg x = log_10 x) și logaritmul natural (ln x = log_e x, unde e ≈ 2,71).

Proprietățile esențiale ale logaritmilor:

• log_a 1 = 0
• log_a a = 1
• log_a x^n = n · log_a x
• log_a (x · y) = log_a x + log_a y
• log_a $x/y$ = log_a x - log_a y

Pentru schimbarea bazei logaritmului, folosește formulele:

• log_a b = log_c b / log_c a
• log_a b = 1 / log_b a

💡 Reține că monotonia funcției logaritmice depinde de baza a: dacă a ∈ (0,1), funcția este strict descrescătoare, iar dacă a > 1, funcția este strict crescătoare.

Similar, funcția exponențială f(x) = a^x este strict descrescătoare pentru a ∈ (0,1) și strict crescătoare pentru a > 1.

Funcții - definiții și notații fundamentale

Înțelegerea funcțiilor începe cu notația formală: f: A → B, x ↦ f(x), unde A este domeniul funcției și B este codomeniul. Graficul funcției (Gf) conține toate perechile (x, f(x)) unde x este din domeniul funcției.

Când lucrezi cu graficul unei funcții, e important să determini intersecțiile cu axele de coordonate:

• Cu axa Ox: rezolvă ecuația f(x) = 0
• Cu axa Oy: calculează valoarea f(0)

Pentru a găsi punctele de intersecție a două grafice Gf și Gg:

1. Rezolvă ecuația f(x) = g(x) pentru a determina abscisa
2. Calculează ordonata folosind valorile găsite pentru x

💡 Compunerea funcțiilor este o operație fundamentală: (f ∘ g)(x) = f(g(x)). Asigură-te că domeniul funcției g include valorile necesare pentru f.

Vei întâlni frecvent acest concept în probleme complexe, unde trebuie să aplici consecvențe multiple de funcții.

Funcții - clasificare și proprietăți

Funcțiile pot fi clasificate după mai multe criterii, fiecare cu proprietăți specifice care te ajută să le analizezi.

Funcții pare și impare: Pentru o funcție f definită pe o mulțime simetrică A:

• f este pară dacă f$-x$ = f(x) pentru orice x din A
• f este impară dacă f$-x$ = -f(x) pentru orice x din A

Funcții periodice: O funcție f este periodică cu perioada T dacă f$x + T$ = f(x) pentru orice x din domeniu. Cea mai mică perioadă pozitivă nenulă se numește perioadă principală.

Imaginea unei funcții reprezintă mulțimea tuturor valorilor pe care le ia funcția: Im f = {f(x) | x ∈ A}.

💡 O funcție este injectivă dacă valori diferite din domeniu produc valori diferite în codomeniu. Acest lucru este echivalent cu: f(x₁) = f(x₂) implică x₁ = x₂.

O funcție este surjectivă dacă orice element din codomeniu este imaginea cel puțin a unui element din domeniu. Când o funcție este atât injectivă cât și surjectivă, ea este bijectivă și are o funcție inversă.

Funcțiile monotone au comportament predictibil:

• Crescătoare: x₁ < x₂ implică f(x₁) ≤ f(x₂)
• Strict crescătoare: x₁ < x₂ implică f(x₁) < f(x₂)
• Descrescătoare: x₁ < x₂ implică f(x₁) ≥ f(x₂)
• Strict descrescătoare: x₁ < x₂ implică f(x₁) > f(x₂)

Funcția de gradul I

Funcția de gradul I (sau funcția liniară) este una dintre cele mai simple și mai utilizate funcții în matematică. Forma ei generală este f(x) = ax + b, unde a și b sunt numere reale, cu a ≠ 0.

Monotonia funcției depinde de valoarea lui a:

• Dacă a > 0, funcția este strict crescătoare (graficul urcă de la stânga la dreapta)
• Dacă a < 0, funcția este strict descrescătoare (graficul coboară de la stânga la dreapta)

Pentru a determina semnul funcției, rezolvă ecuația f(x) = 0, care dă soluția x = -b/a. Apoi poți analiza comportamentul funcției:

| x | -∞ | -b/a | +∞ | |:--:|:--:|:--:|:--:| | f(x) | semn contrar lui a | 0 | semn lui a |

💡 Graficul funcției de gradul I este o dreaptă. Punctul unde dreapta intersectează axa Ox are coordonatele $-b/a, 0$, iar punctul de intersecție cu axa Oy are coordonatele (0, b).

Funcția de gradul I este bijectivă, ceea ce înseamnă că are o funcție inversă bine definită. Această proprietate o face deosebit de utilă în rezolvarea multor tipuri de ecuații și probleme practice.

Funcția de gradul al doilea

Funcția de gradul al doilea, f(x) = ax² + bx + c (a ≠ 0), are ca grafic o parabolă. Înțelegerea comportamentului ei începe cu determinarea vârfului parabolei, punctul extrem cu coordonatele V$-b/2a, -Δ/4a$, unde Δ = b² - 4ac.

Tipul extremului depinde de semnul lui a:

• Dacă a < 0, funcția are un punct de maxim cu valoarea maximă f_max = -Δ/4a
• Dacă a > 0, funcția are un punct de minim cu valoarea minimă f_min = -Δ/4a

Axa de simetrie a parabolei are ecuația x = -b/2a, fiind o dreaptă verticală ce trece prin vârful parabolei.

💡 Relația dintre Δ și intersecțiile cu axa Ox este esențială: dacă Δ > 0, parabola intersectează axa Ox în două puncte; dacă Δ = 0, parabola este tangentă la axa Ox; dacă Δ < 0, parabola nu intersectează axa Ox.

Monotonia funcției depinde de poziția vârfului:

• Pentru a > 0: funcția este strict descrescătoare pe $-∞, -b/2a] și strict crescătoare pe [-b/2a, +∞$
• Pentru a < 0: funcția este strict crescătoare pe $-∞, -b/2a] și strict descrescătoare pe [-b/2a, +∞$

Imaginea funcției este:

• Im f = [-Δ/4a, +∞) când a > 0
• Im f = (-∞, -Δ/4a] când a < 0

Ecuații iraționale, exponențiale și logaritmice

Ecuațiile iraționale conțin necunoscute sub radical. Metoda standard de rezolvare este:

Pentru ecuații de forma √f(x) = g(x):

1. Stabilește condițiile de existență: f(x) ≥ 0 și g(x) ≥ 0
2. Ridică la pătrat ambele părți: f(x) = g(x)²
3. Rezolvă ecuația rezultată și verifică soluțiile

Pentru ecuații cu radical de ordin 3 $√³f(x) = g(x)$, nu există condiții de existență pentru radical, dar procedura implică ridicarea la cub.

Ecuațiile exponențiale pot fi rezolvate prin mai multe metode:

• Dacă a^f(x) = a^g(x), atunci f(x) = g(x) (baza a aceeași)
• Dacă a^f(x) = b, atunci f(x) = log_a b
• Prin folosirea proprietăților puterilor

💡 La ecuațiile logaritmice, nu uita niciodată să verifici condițiile de existență: argumentul logaritmului trebuie să fie pozitiv, iar baza trebuie să fie pozitivă și diferită de 1.

Ecuațiile logaritmice se rezolvă prin:

• Dacă log_a f(x) = log_a g(x), atunci f(x) = g(x), cu condiția ca f(x) > 0 și g(x) > 0
• Dacă log_a f(x) = N, atunci f(x) = a^N
• Prin aplicarea proprietăților logaritmilor

Ecuații trigonometrice

Ecuațiile trigonometrice necesită o bună înțelegere a formulelor fundamentale și a periodicității funcțiilor trigonometrice.

Ecuațiile trigonometrice fundamentale au soluții generale:

• sin x = a $unde a ∈ [-1,1]$: x = (-1)^k arcsin a + kπ, k ∈ Z
• cos x = a $unde a ∈ [-1,1]$: x = ±arccos a + 2kπ, k ∈ Z
• tg x = a (a ∈ R): x = arctg a + kπ, k ∈ Z
• ctg x = a (a ∈ R): x = arcctg a + kπ, k ∈ Z

Pentru ecuații de forma sin(f(x)) = sin(g(x)), avem soluția generală: f(x) = (-1)^k · g(x) + kπ, k ∈ Z

Pentru cos(f(x)) = cos(g(x)), soluția este: f(x) = ±g(x) + 2kπ, k ∈ Z

💡 Când folosești substituția tg$x/2$ = t pentru a rezolva ecuații de forma a·cos x + b·sin x + c = 0, verifică întotdeauna și valorile x = $2k+1$π, deoarece acestea pot fi pierdute în proces.

Ecuațiile trigonometrice complexe pot fi rezolvate adesea folosind formule precum:

• sin²x + cos²x = 1
• cos 2x = cos²x - sin²x = 1 - 2sin²x

Pentru ecuațiile trigonometrice liniare $a·cos x + b·sin x + c = 0$, o metodă eficientă este utilizarea substituției tg$x/2$ = t și formulele de transformare.

Matematici financiare

Matematica financiară îți oferă instrumente pentru a calcula modificări ale prețurilor, dobânzi și taxe - concepte esențiale pentru viața reală.

Calculul procentelor se face cu formula: p% din x = $p/100$ · x. De exemplu, 20% din 150 lei = 0,2 · 150 = 30 lei.

Pentru scumpirea unui produs cu p%, prețul final se calculează: p_final = x + $p/100$ · x, unde x este prețul inițial. Similar, pentru reducerea cu p%, folosim: p_final = x - $p/100$ · x.

Taxa pe valoarea adăugată (TVA) se adaugă la prețul de producție: p_v = x + $p/100$ · x, unde p este procentul TVA. Valoarea TVA-ului este diferența: TVA = p_v - x.

💡 Dobânda compusă crește mult mai rapid decât dobânda simplă pe perioade lungi. De exemplu, 1000 lei la o dobândă de 5% pe an va aduce 250 lei în 5 ani cu dobândă simplă, dar aproape 276 lei cu dobândă compusă.

Dobânda simplă se calculează: D = S · $r/100$ · n, unde S este suma inițială, r este rata dobânzii (%) și n este perioada în ani. Suma finală este: S_finală = S + D.

Dobânda compusă consideră că dobânda se adaugă la capital periodic: D = S · $(1 + r/100)^n - 1$ și S_finală = S · $1 + r/100$^n. Această formulă reflectă cum dobânda se aplică și asupra dobânzii acumulate anterior.

Geometrie analitică în plan

Geometria analitică îți permite să lucrezi cu figuri geometrice folosind coordonate și ecuații.

Pozițiile relative a două drepte se determină astfel:

• Pentru drepte date prin panta lor: d₁ ∥ d₂ ⟺ m_d₁ = m_d₂ și d₁ ⊥ d₂ ⟺ m_d₁ · m_d₂ = -1
• Pentru drepte date prin ecuații generale $a₁x + b₁y + c₁ = 0 și a₂x + b₂y + c₂ = 0$:
  • Drepte concurente (se intersectează): a₁/a₂ ≠ b₁/b₂
  • Drepte paralele: a₁/a₂ = b₁/b₂ ≠ c₁/c₂
  • Drepte coincidente: a₁/a₂ = b₁/b₂ = c₁/c₂

Aria unui triunghi cu vârfurile A$x_A, y_A$, B$x_B, y_B$ și C$x_C, y_C$ se calculează cu formula: A_△ABC = (1/2)|Δ|, unde Δ este determinantul.

💡 Distanța de la un punct A$x_A, y_A$ la o dreaptă d: ax + by + c = 0 se calculează cu formula: d(A,d) = |ax_A + by_A + c|/√$a² + b²$. Această formulă este esențială pentru rezolvarea multor probleme geometrice.

Coliniaritatea a trei puncte A, B și C se verifică dacă determinantul Δ = 0. Acest concept este fundamental pentru a verifica dacă trei puncte se află pe aceeași dreaptă.

Centrul de greutate al unui triunghi ABC are coordonatele: x_G = $x_A + x_B + x_C$/3 și y_G = $y_A + y_B + y_C$/3. Acesta este punctul de intersecție al medianelor triunghiului.